시간 복잡도 O(입력)
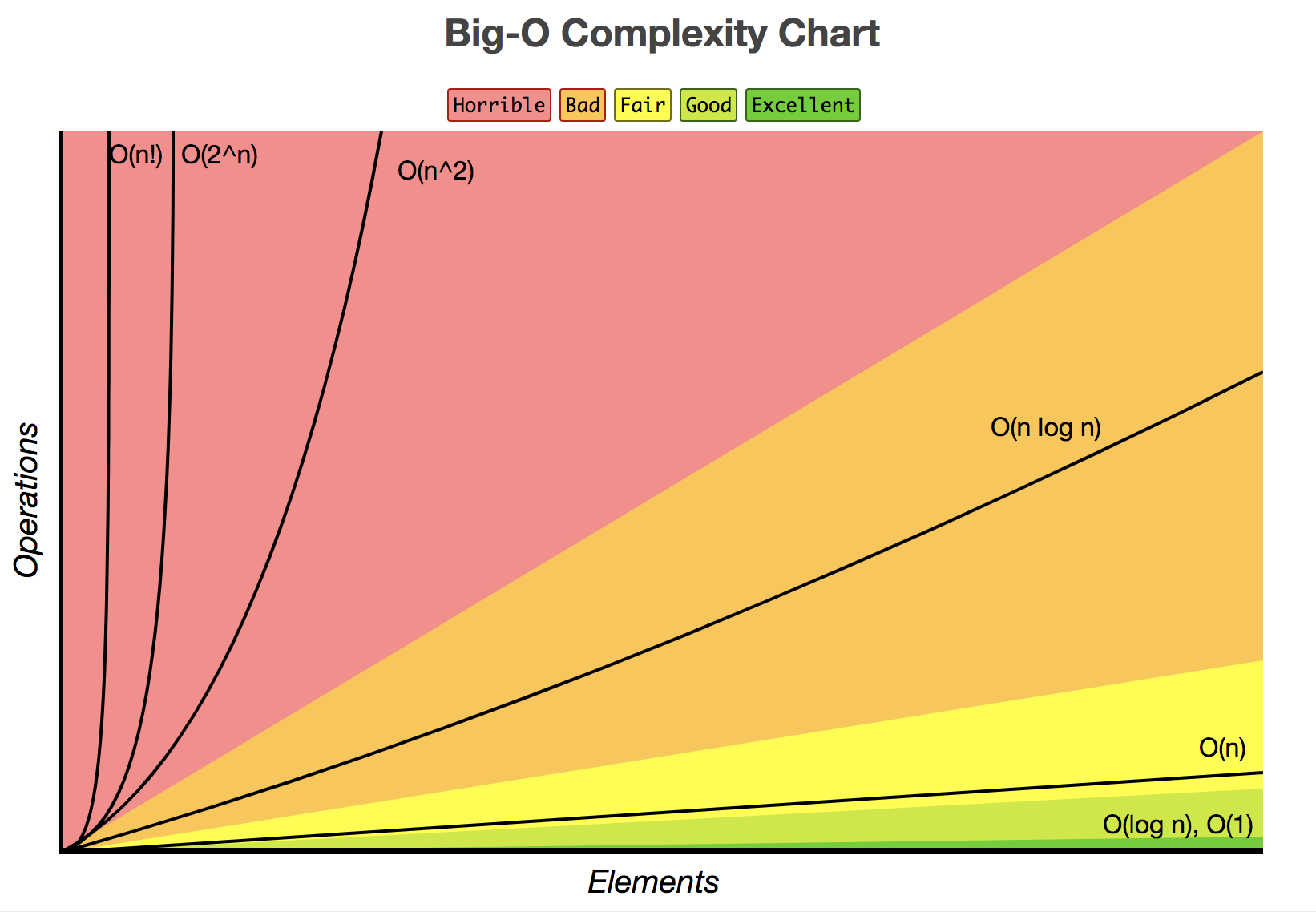
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(2^2) < O(n!)
오른쪽으로 갈 수록 실행 횟수가 많은, 시간 복잡도가 높은 것이다.
O(1)
var n = [];
// n에 계속적으로 숫자 대입
function o1() {
return (n[0] === 0) ? true : false;
}
// 데이터가 증가해도 위 function o1 function의 성능은 그대로다.O(n)
let n = [];
for (let i = 0; i < n.length; i++) {
return n[i]
}
// 배열의 n의 길이가 증가할 때마다 처리 시간이 증가한다.입력n만큼 출력을 반복하는 반복문
O(n^2)
let n = [];
for(let i = 0; i < n.length; i++) {
for(var j = 0; j < n.length; j++) {
console.log(i + j);
}
}
// 배열 n의 length가 증가 할 때마다 처리 시간 제곱배로 증가반복문 두 개가 중첩되어 실행되어 있어, n이 10이면 100번이 실행될 것.
코드를 추가하고 변수도 선언하고 해서 3n^2+129018이 되더라도 중요한 것은 최고차항
O(log N)
// 리턴의 숫자는 몇번의 스캔을 통해 값을 찾는지 말한다.
// k는 정답, arr = 스캔 배열, s는 배열의 처음, e는 배열의 마지막
var arr = [];
function log(k, s, e) {
for(var i = s; i <= e; i++) {
arr.push(i);
let m = (s+e)/2;
if(arr[m] === k){
console.log(m)
} else if(arr[m] > k) {
return log(k, s, m-1);
} else {
return log(k, m+1, e);
}
}
}데이터가 증가해도 성능이 크게 차이나지 않는다.
업다운 게임처럼, 100숫자중 50을 찾고 업을 외치면 밑에 숫자는 버려지는 형식
대규모 컬렉션을 처리할 때 가장효율적인 방법이다.
대표적으로 이진탐색(binary search), 퀵정렬, 병합정렬 등이 있음
function FindItemBinarySearch(items, match) {
var low = 0,
high = items.length -1;
while (low <= high) {
mid = parseInt((low + high) / 2);
current = items[mid];
if (current > match) {
high = mid - 1;
} else if (current < match) {
low = mid + 1;
} else {
return mid;
}
}
return -1;
}
const quickSort = list => {
if (list.length < 2)
return list;
let pivot = list[0];
let left = [];
let right = [];
for (let i = 1, total = list.length; i < total; i++){
if (list[i] < pivot)
left.push(list[i]);
else
right.push(list[i]);
}
return [
...quickSort(left),
pivot,
...quickSort(right)
];
};
quickSort([1,2,999,3,4,56,77,8,9,123])
// [1,2,3,4,7,8,56,77,123,999]