
📌 정렬 알고리즘
정렬 알고리즘은 데이터셋이 주어졌을 때, 이를 사용자가 지정한 기준에 맞게 정렬하여 출력하는 알고리즘이다. 정렬 알고리즘에는 대표적으로 선택정렬, 삽입정렬, 버블정렬, 병합정렬, 퀵정렬, 힙정렬 이있다.
컴퓨터는 많은 양의 데이터를 다룬다. 데이터베이스의 경우 이론상 무한 개의 데이터를 다룰 수 있어야 한다. 이렇게 많은 양의 불규칙한 데이터들을 정렬 후 탐색해야 하는 경우, 상황에 맞는 알고리즘을 사용하여 효과적으로 문제를 해결하는 것이 핵심이다.
대표적인 정렬 알고리즘에는 선택정렬, 삽입정렬, 버블정렬, 병합정렬, 퀵정렬, 힙정렬이 있으며 이 알고리즘들의 성능은 빅오표기법으로 표현한다.
1. 선택정렬(Selection Sort)
선택정렬은 주어진 데이터들 중 현재 위치에 맞는 데이터를 선택해 위치를 교환하는 정렬 알고리즘이다. 의 시간복잡도를 가지고 있다.

기본 로직은 다음과 같다.
1. 0~n번 인덱스에서 최솟값을 찾아 0번 인덱스와 바꾼다.
2. 1~n번 인덱스에서 최솟값을 찾아 1번 인덱스와 바꾼다.
...
3. n-1~n번 인덱스에서 최솟값을 찾아 n-1번 인덱스와 바꾼다.
선택정렬은 전체 리스트를 순회해가며 검사하기 때문에 한결같이 의 시간복잡도를 가진다.
▶ 선택정렬 구현 [Python]
def selection_sort(arr):
for i in range(len(arr) - 1):
min_idx = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]2. 삽입정렬(Insertion Sort)
삽입정렬은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다. 의 시간복잡도를 가지고 있다.
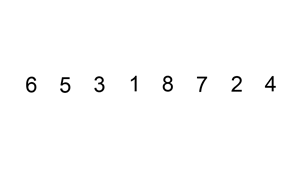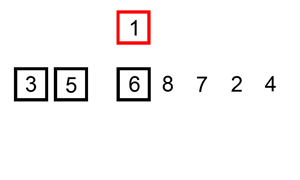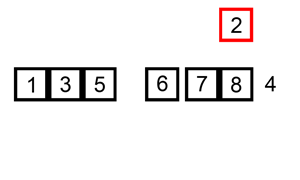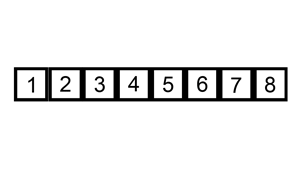
삽입정렬은 버블정렬과 비교하여 더 빠르며, 정렬되어있는 배열일수록 효율이 높아지게 된다.
모두 정렬되어있는 최선의 경우에는 시간복잡도가 O(n)이 된다.
삽입정렬의 기본 로직은 다음과 같다.
1. 두 번째 인덱스가 첫 번째 인덱스와 자신을 비교하고, 자신이 더 크면 비교를 멈추고 다음 인덱스로 넘어갑니다.
2. 만약, 자신이 더 작다면 앞에 있던 원소를 한 칸 뒤로 밀고, 자신은 그보다 한 칸 더 앞에 있던 원소와 비교를 진행합니다.
3. 앞보다 내가 더 커서 더이상 비교를 진행하지 않아도 되면 비어있는 칸에 자신을 위치시킵니다. ※ 삽입정렬은 버블정렬처럼 교환하지 않고, '삽입'합니다.
▶ 삽입정렬 구현 [Python]
def insert_sort(x):
for i in range(1, len(x)):
j = i - 1
key = x[i]
while x[j] > key and j >= 0:
x[j+1] = x[j]
j = j - 1
x[j+1] = key
return x3. 버블정렬(Bubble Sort)
버블정렬은 두 인접한 원소를 검사하여 정렬하는 방법이다. 의 시간복잡도를 가져 상당히 느리지만, 코드가 단순하기 때문에 자주 사용된다.
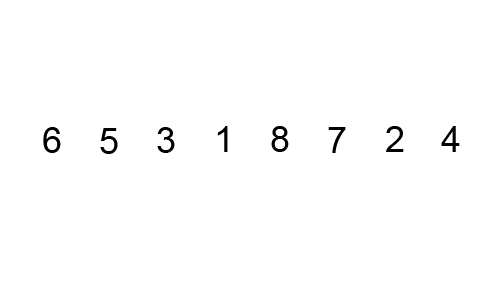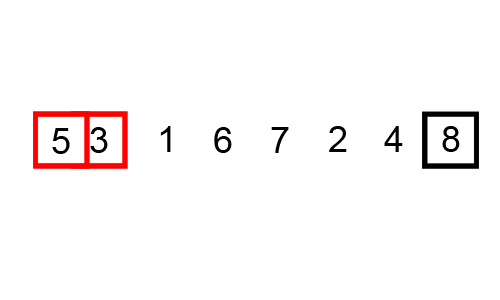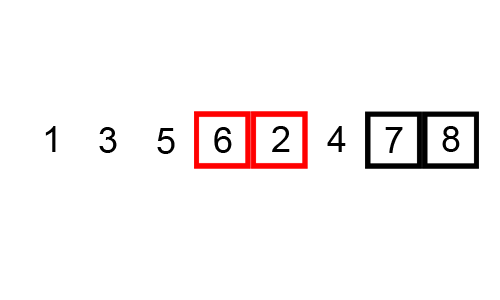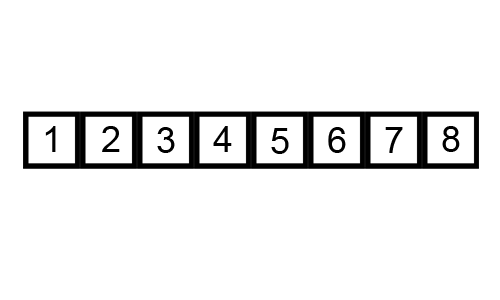
버블정렬의 기본 로직은 다음과 같다.
1. 0번째 원소와 1번째 원소를 비교 후 정렬
2. 1번째 원소와 2번째 원소를 비교 후 정렬
...
3. n-1번째 원소와 n번째 원소를 비교 후 정렬
4. 1~3번 과정까지 순회가 한 번 끝나면 가장 큰 수가 맨 끝으로 이동한다.
5. 두 번째 순회부터는 가장 끝 원소를 제외하고 1~3번 과정을 반복한다.
6. 두 번째 순회 때는 비교한 원소 중 가장 큰 원소가 맨 끝의 두 번째 자리로 이동한다.
7. 순회가 끝날때까지 반복예를들어 [7, 4, 5, 1, 3]배열을 오름차순으로 정렬하는 버블정렬의 과정은 다음과 같다.
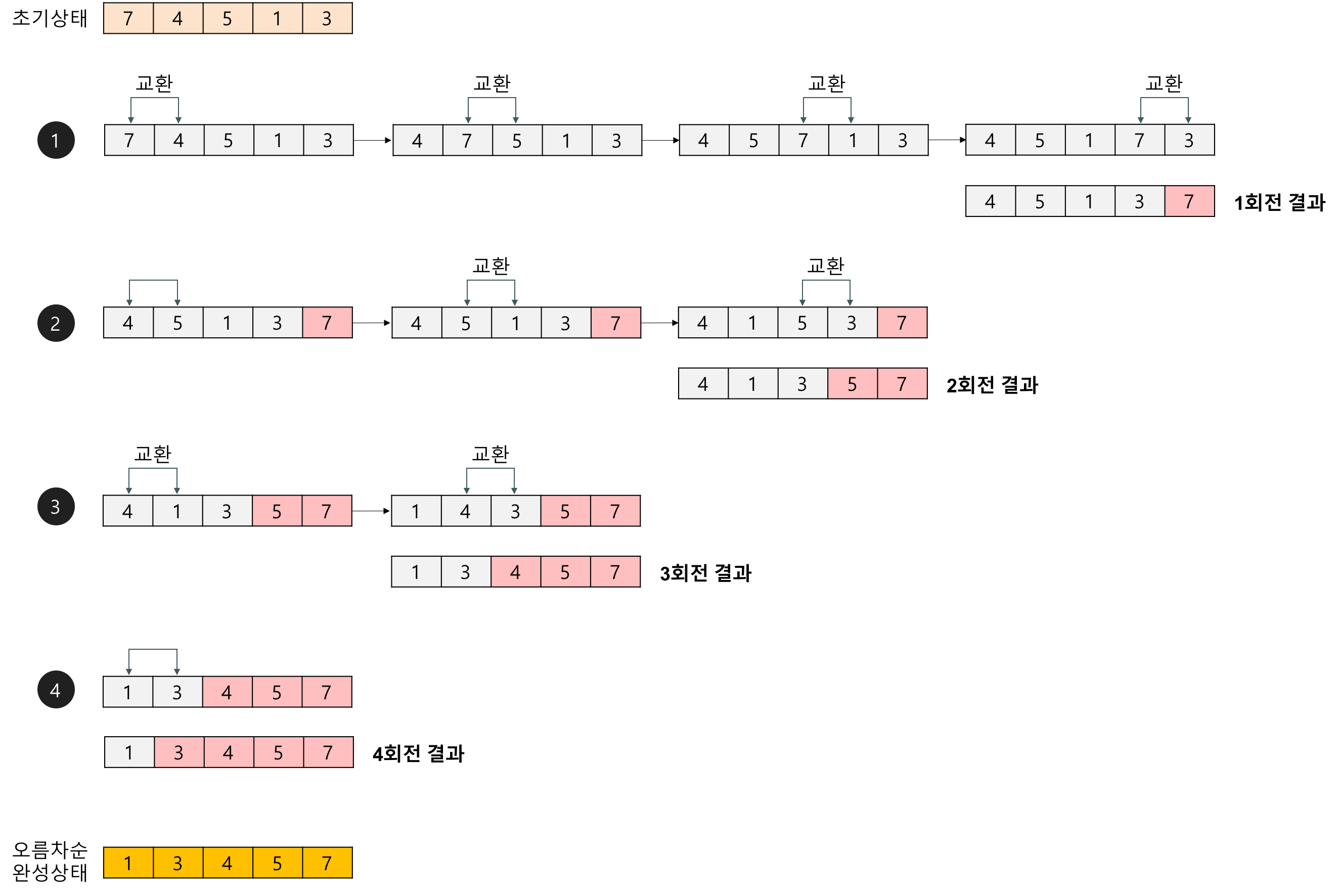
※ 제일 작은 값을 찾아 맨 앞에 위치시키는 선택정렬과는 반대의 정렬 방향을 갖는다.
1회전에서 가장 큰 자료가 맨 끝으로 이동하므로, 2회전부터는 가장 끝 자료를 비교하지 않는다.
마찬가지로 2회전에서 비교한 자료 중 가장 큰 자료가 끝에서 두 번째에 놓이므로, 3회전부터는 끝에서 두 번째까지의 자료를 비교할 필요가 없다.
▶ 버블정렬 구현 [Python]
def bubbleSort(x):
length = len(x)-1
for i in range(length):
for j in range(length-i):
if x[j] > x[j+1]:
x[j], x[j+1] = x[j+1], x[j]
return x4. 병합정렬(Merge Sort)
병합정렬은 주어진 배열의 크기가 1이 될 때 까지 쪼갠 후 작은 단위부터 정렬하여 정렬된 단위들을 계속 병합해가며 정렬하는 방법이다. 분할 정복 기법과 재귀함수를 이용하며, O(nlogn)의 시간복잡도를 가지기 때문에 효율적이다. 하지만, 데이터 전체 크기만한 메모리가 더 필요해 O(n)의 공간복잡도를 가진다.
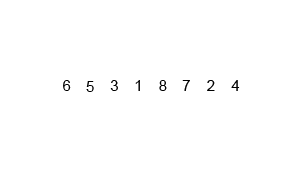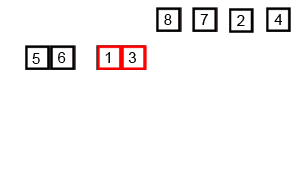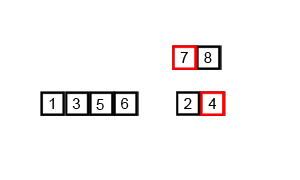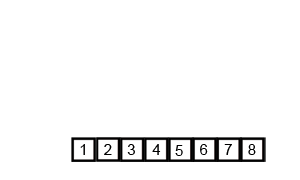
병합정렬의 기본 로직은 다음과 같다.
[6, 5, 3, 1, 8, 7, 2, 4]의 배열을 오름차순으로 병합정렬 한다고 가정해보자.
1. 더이상 쪼개지지 않을 작은 단위로 쪼갠다.
[6], [5], [3], [1], [8], [7], [2], [4]
2. 배열을 두 개씩 합친다. 합칠 때는 큰 수가 뒤로 가도록 정렬한다.
[5, 6], [1, 3], [7, 8], [2, 4]
3. 배열을 두 개씩 합친다. 합칠 때는 큰 수가 뒤로 가도록 정렬한다.
[1, 3, 5, 6], [2, 4, 7, 8]
4. 배열을 두 개씩 합친다. 합칠 때는 큰 수가 뒤로 가도록 정렬한다.
[1, 2, 3, 4, 5, 6, 7, 8]▶ 병합정렬 구현 [Python]
def merge_sort(arr):
if len(arr) < 2:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
merged_arr = []
l = h = 0
while l < len(left) and h < len(right):
if left[l] < right[h]:
merged_arr.append(left[l])
l += 1
else:
merged_arr.append(right[h])
h += 1
merged_arr += left[l:]
merged_arr += right[h:]
return merged_arr💡 병합정렬 구현 이해
병합정렬을 처음 접한다면 구현 부분이 쉽지 않을 것입니다.
먼저 재귀함수에 대한 이해가 부족하다면 아래링크를 참고하시기 바랍니다.
https://velog.io/@falling_star3/Python-재귀함수Recursive-Function
말로 적어내기 어려워 위 코드의 로직을 손코딩으로 풀이했습니다.
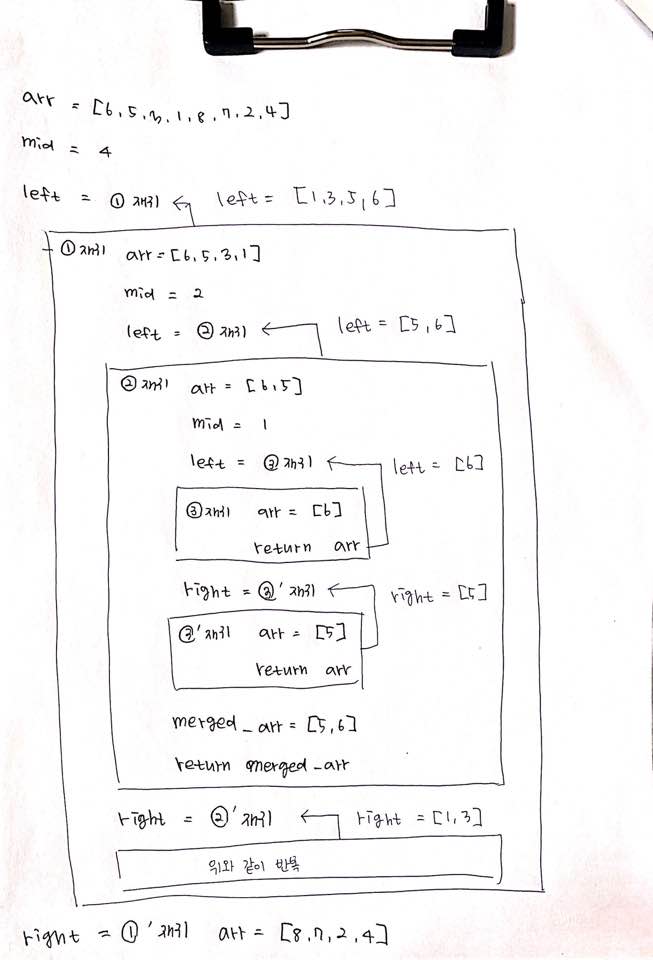
다음은 코드의 순서에 따른 변수값입니다.
left [6]
right [5]
merged: [5, 6]
left [3]
right [1]
merged: [1, 3]
left [5, 6]
right [1, 3]
merged: [1, 3, 5, 6]
left [8]
right [7]
merged: [7, 8]
left [2]
right [4]
merged: [2, 4]
left [7, 8]
right [2, 4]
merged: [2, 4, 7, 8]
left [1, 3, 5, 6]
right [2, 4, 7, 8]
merged: [1, 2, 3, 4, 5, 6, 7, 8]5. 퀵정렬(Quick Sort)
연속적인 분할에 의한 정렬방법이다. 처음 하나의 축(Pivot)을 먼저 정하여 이 축의 값보다 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 위치시킨 뒤 왼쪽과 오른쪽의 수 들을 다시 각각의 축으로 나누어 축값이 1이 될 때까지 정렬한다. O(nlogn)의 시간복잡도를 가진다.
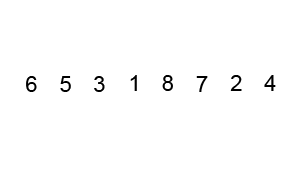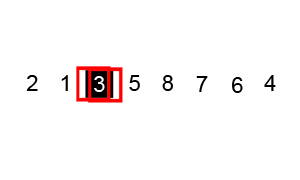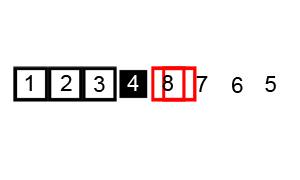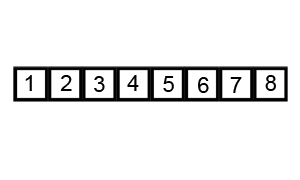
퀵정렬의 기본 로직은 다음과 같다.
1. 입력된 자료 리스트에서 하나의 원소를 고른다. 이 원소를 '피벗'이라고 부른다.
2. 피벗을 기준으로 리스트를 둘로 분할한다.
3. 피벗을 기준으로 피벗조다 작은 원소들은 모두 피벗의 왼쪽으로 옮긴다.
4. 피벗을 기준으로 피벗보다 큰 원소들은 모두 피벗의 오른쪽으로 옮긴다.▶ 퀵정렬 구현 [Python]
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
lesser_arr, equal_arr, greater_arr = [], [], []
for num in arr:
if num < pivot:
lesser_arr.append(num)
elif num > pivot:
greater_arr.append(num)
else:
equal_arr.append(num)
return quick_sort(lesser_arr) + equal_arr + quick_sort(greater_arr)6. 힙정렬(Heap Sort)
힙정렬은 최대 힙트리나 최소 힙트리를 구성해 정렬하는 방법이다. 내림차순 정렬을 위해서는 최대 힙을 구성하고, 오른차순 정렬을 위해서는 최소 힙을 구성한다. O(nlogn)의 시간복잡도를 가지며 같은 시간복잡도를 가지는 알고리즘 중 부가적인 메모리가 필요없다는 장점을 가진다.

힙정렬의 기본 로직은 다음과 같다.
1. 주어진 자료를 힙 구조로 만든다. 힙 성질을 만족하도록 하는 연산을 heapify라 한다.
(힙 구조: 완전이진트리로, 다음 속성을 만족한다.
최대 힙: 각 노드의 값은 자신의 자식노드가 가진 값보다 크거나 같다.
최소 힙: 각 노드의 값은 자신의 자식노드가 가진 값보다 작거나 같다.)
2. 최대(최소) 힙의 루트노드를 말단노드와 교환한다.
3. 새 루트노드에 대해 최대(최소) 힙을 구성한다.
4. 원소의 개수만큼 2와 3을 반복 수행한다.▶ 힙정렬 구현 [Python]
def heapify(unsorted, index, heap_size):
largest = index
left_index = 2 * index + 1
right_index = 2 * index + 2
if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
largest = left_index
if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
largest = right_index
if largest != index:
unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
heapify(unsorted, largest, heap_size)
def heap_sort(unsorted):
n = len(unsorted)
# BUILD-MAX-HEAP (A) : 위의 1단계
# 인덱스 : (n을 2로 나눈 몫-1)~0
# 최초 힙 구성시 배열의 중간부터 시작하면 이진트리 성질에 의해 모든 요소값을 서로 한번씩 비교할 수 있게 됨 : O(n)
for i in range(n // 2 - 1, -1, -1):
heapify(unsorted, i, n)
# Recurrent (B) : 2~4단계
# 한번 힙이 구성되면 개별 노드는 최악의 경우에도 트리의 높이(logn)만큼의 자리 이동을 하게 됨. 이런 노드들이 n개 있으므로 : O(nlogn)
for i in range(n - 1, 0, -1):
unsorted[0], unsorted[i] = unsorted[i], unsorted[0]
heapify(unsorted, 0, i)
return unsorted위에서 다루지 않은 정렬 중 쉘정렬(Shell Sort)과 기수정렬(Radix Sort)이 있다.
쉘정렬은 삽입정렬의 개념을 확대하여 일반화한 정렬방법이다.
기수정렬은 데이터의 비교를 통한 정렬이 아닌 분산 정렬을 이용한 정렬방법이며 자릿수가 있는 데이터(정수, 문자열 등)에만 사용 가능하다.
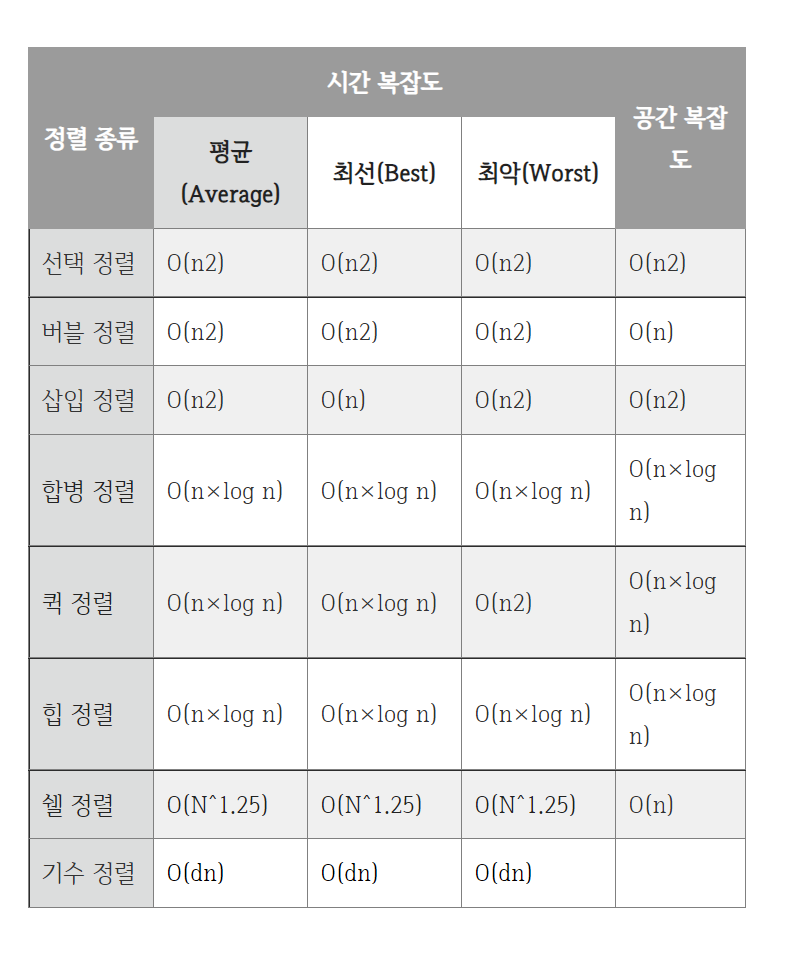
7. 정렬 별 비교
▶ 정렬 별 시간복잡도, 공간복잡도 비교
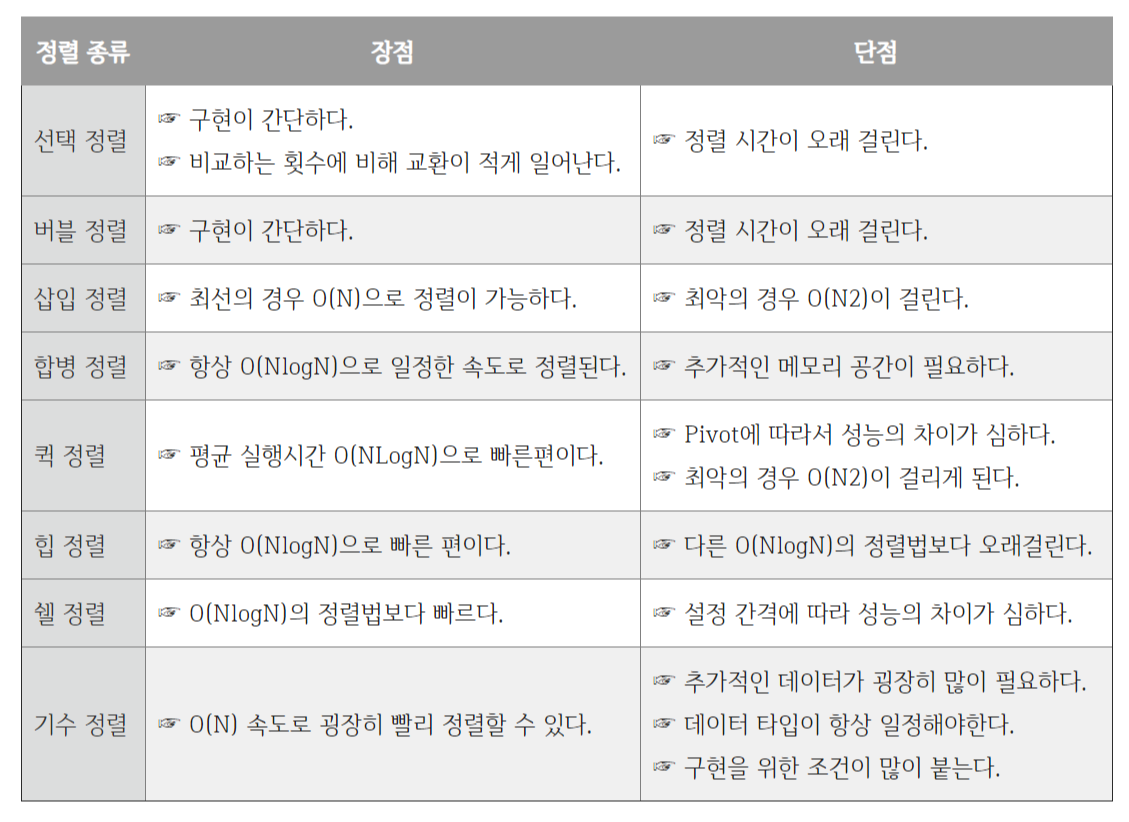
▶ 정렬 별 장단점 비교
Reference
https://coding-factory.tistory.com/615?category=794828
https://github.com/TheAlgorithms/Python/blob/master/sorts/heap_sort.py
