
📌 이진트리(Binary Tree)의 개념과 이해
1. 이진트리(Binary Tree)란?
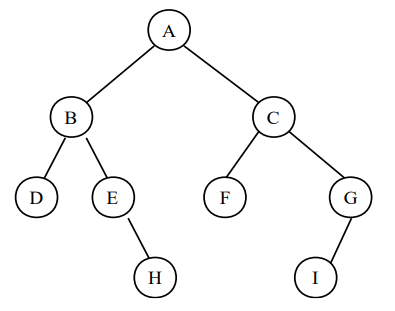
트리의 종류 중 하나로 모든 노드의 자식 노드가 최대 2개인 트리를 의미한다.
포화 이진 트리 (Full Binary Tree), 완전 이진 트리 (Complete Binary Tree) 등의 종류가 있다.
2. 이진트리의 목적
이진 트리는 탐색 및 효율적인 검색, 삽입, 삭제가 필요할 때 유용하다.
이진 트리 탐색의 시간 복잡도는 평균적으로 O(log n)이기 때문이다.
(트리가 한쪽으로 치우치면 시간 복잡도는 O(n)이 될 수 있다.)
✅ 효율적인 탐색과 정렬
이진 탐색 트리(BST)를 활용하면 평균적인 탐색, 삽입, 삭제 연산이 O(logn)으로 매우 빠름. 이진 힙(Binary Heap)을 활용하면 정렬 및 우선순위 관리가 쉬움.
✅ 메모리 효율적인 구조
배열이나 리스트보다 메모리를 절약하면서 동적 크기 조정이 가능.
트리 구조는 연결 리스트처럼 필요할 때만 메모리를 사용함.
✅ 재귀적 구조로 문제 해결 가능
트리는 자연스럽게 재귀를 활용할 수 있어 많은 알고리즘 설계에 유리함.
3. 이진트리의 이해 ✨

이진트리가 왜 검색에 빠르다는 걸까?
이진트리를 이해하지 못하면 이진트리의 목적과 활용을 이해할 수 없다.
간단한 예시를 들어보겠다.
누군가 당신에게 물어본다.
???: 1~100사이에서 내가 생각한 숫자 한가지를 맞춰봐라.
숫자를 말하면 나는 Up 또는 Down을 알려주겠다.
나: 50
???: 다운
나: 25
???: 다운
나: 12당신은 첫번째로 무슨 숫자를 부를 것인가?
나는 딱 절반인 50을 부르겠다.
그 이후에도 절반을 부르겠다.
이렇게 범위를 좁혀나가는 것이다.
이것이 바로 이진탐색 트리를 이해하는 첫번째이다.
이제 이진트리를 이해하기 위해 배열을 이진탐색트리로 구현하는 예시를 살펴보자.
▶ 배열을 이진탐색 트리로 만드는 예제 🐭
① 배열 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 가 있다.
② '2'는 어디(인덱스)있는가?
③ 이진 검색 트리로 찾아보자.
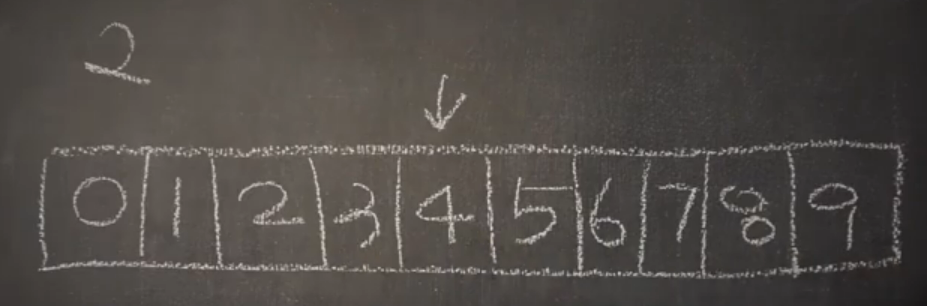
중앙값이 '4', '5'인데 이 중 작은수를 뽑는 규칙을 설정하겠다.
'4'를 뽑았다.
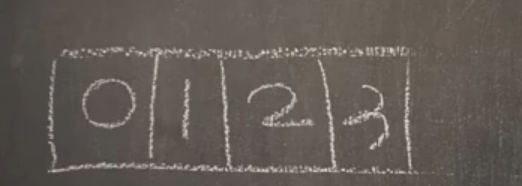
우리가 찾으려는 '2'는 '4'보다 작으므로 '4'의 왼쪽만 보겠다.
(오른쪽은 이제 볼 필요가 없다.)
'0', '1', '2', '3' 이 있다. 여기서 또 중앙값을 찾는다.
'1'과 '2'중 작은수를 뽑는 규칙을 정했으므로 '1'이다.
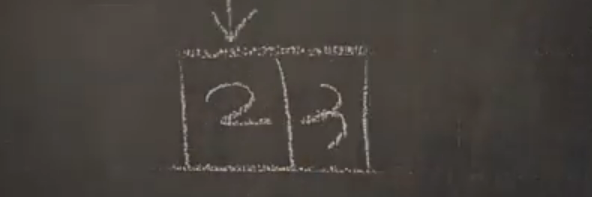
'2'는 '1'보다 크므로 '1'의 오른쪽만 남는다.
'2', '3'이 남았다.
'2'를 찾았다.
이제 위의 탐색법(경로)을 이진트리로 구현해보겠다.
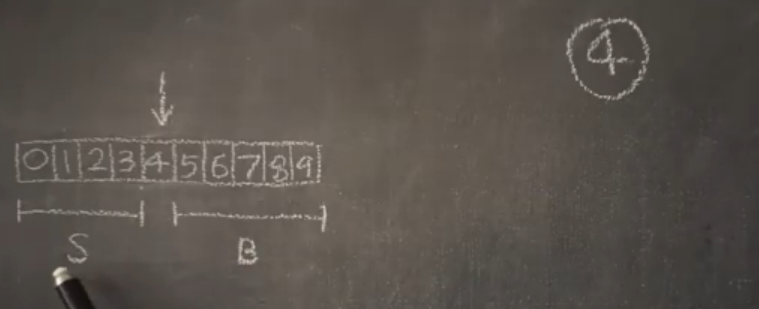
처음 찾은 중앙값인 '4'가 루트노드가 된다.

'4'보다 작은 값들을 탐색한다.
'4'보다 작은 값들이므로 왼쪽 자식 노드로 들어간다.(왼쪽 오른쪽은 다른 노드로 취급한다.)
자식노드는 중앙값인 '1'이 들어간다.
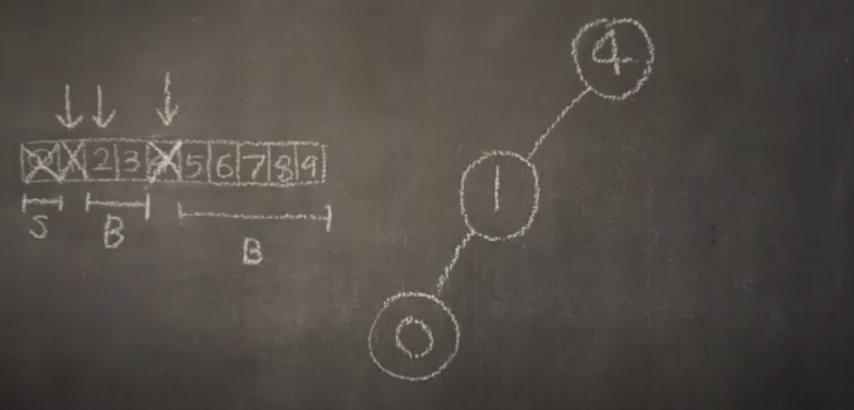
'1'보다 작은 값들을 탐색한다.
'1'보다 작은 값들이므로 왼쪽 자식 노드로 들어간다.
자식노드는 중앙값인 '0'이 들어간다.
'0'보다 작은 값이 없으므로 왼쪽자식 노드 탐색은 끝이난다.
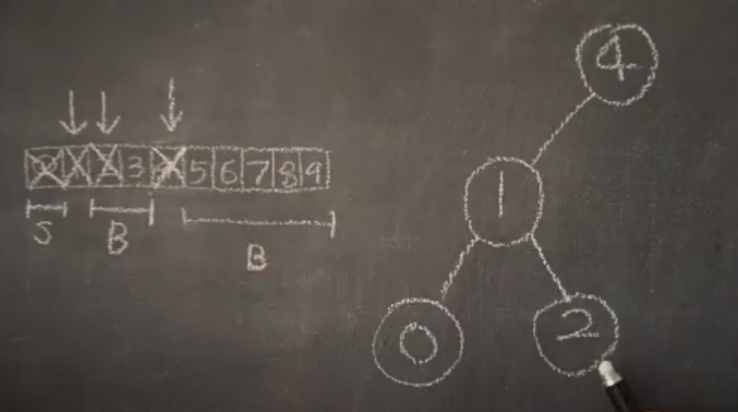
이제 '1'보다 큰 '1'의 오른쪽 자식노드를 탐색한다.
'1'보다 큰 값들이므로 오른쪽 자식 노드로 들어간다.
자식노드는 중앙값인 '2'가 들어간다.
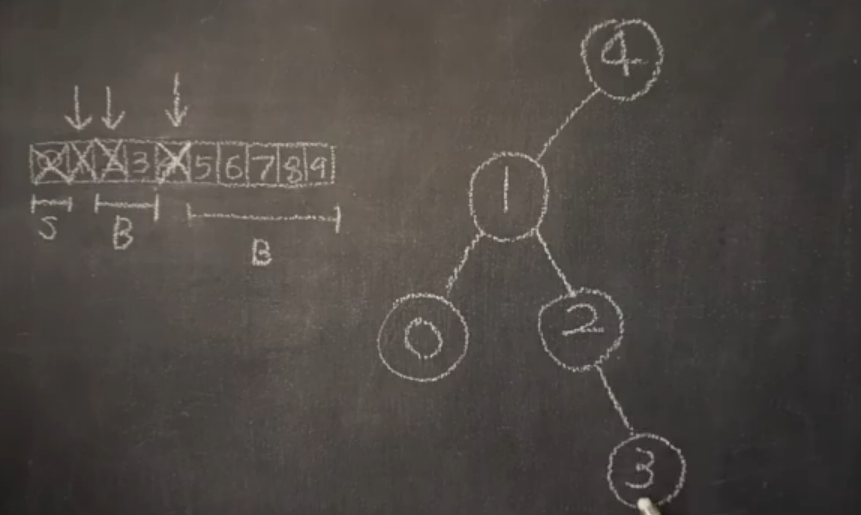
'2'보다 큰 값들을 탐색한다.
'2'보다 큰 값들이므로 오른쪽 자식 노드로 들어간다.
자식노드는 중앙값인 '3'이 들어간다.
'3'보다 큰 값이 없으므로 오른쪽자식 노드 탐색은 끝이난다.
('4'보다 작은 '0', '1', '2', '3'만 탐색했으므로)
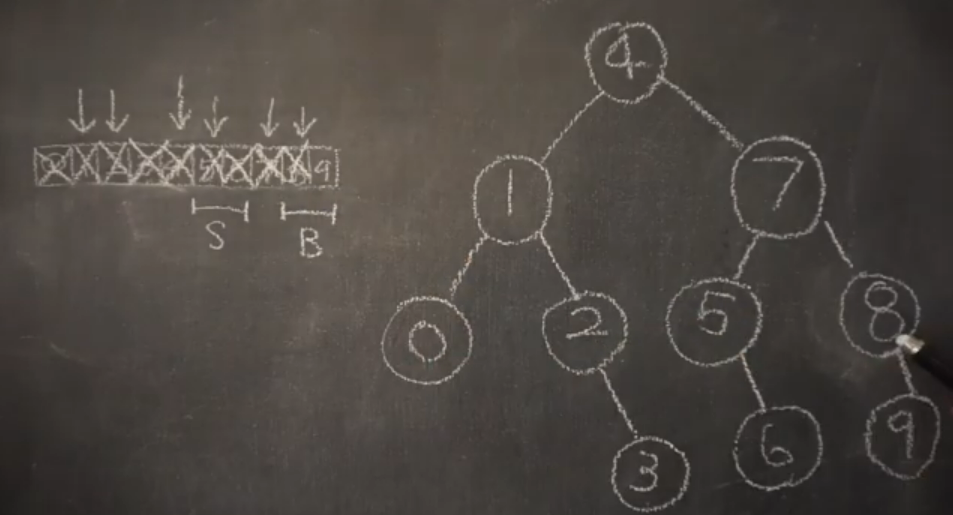
이와같이 '4'의 오른쪽도 탐색하면 위와같은 트리가 완성된다.
👉 유튜브 참고
★ 위의 유튜브에서 영상 자료를 참고하였으며, 강추하는 영상입니다. ★
저렇게 구현된 트리를 노드별로 순회하며 탐색하는 방법을 이진 탐색 트리라한다.
위 예제의 탐색 방법 외에도 여러 탐색 방법이 있고, 여러 트리구조가 있다.
위의 탐색 방법은 '전위 순회'이다. (루트 노드인 '4'부터 자식노드 순회)
탐색 방법을 더 알아보자.
📌 2. 이진트리 탐색 방법(전위·중위·후위·레벨순회)
① 전위 순회 (Preorder Traversal): 루트 → 왼쪽 → 오른쪽
② 중위 순회 (Inorder Traversal): 왼쪽 → 루트 → 오른쪽
③ 후위 순회 (Postorder Traversal): 왼쪽 → 오른쪽 → 루트 (LRV) ✨
④ 레벨 순회 (Levelorder Traversal): 루트부터 레벨별로 왼쪽에서 오른쪽으로 (BFS, 너비 우선 탐색)
탐색 경로에 따라 전위, 중위, 후위, 레벨 순회가 있다.
일반적으로, 후위 순회가 많이 사용된다.
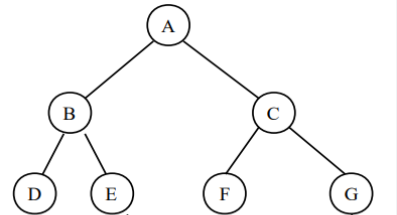
① 전위 순회 (Preorder Traversal): 루트 → 왼쪽 → 오른쪽 (VLR)
👉 A → B → D → E → C → F → G
(1) 자기 자신을 처리
(2) 왼쪽 자식을 방문
(3) 오른쪽 자식을 방문
루트 노드를 가장 먼저 방문하기 때문에 트리 구조를 표현하는 데 적합
→ 디렉터리 탐색, 데이터 직렬화
② 중위 순회 (Inorder Traversal): 왼쪽 → 루트 → 오른쪽 (LVR)
👉 D → B → E → A → F → C → G
(1) 왼쪽 자식을 방문
(2) 자기 자신을 처리
(3) 오른쪽 자식을 방문
이진 탐색 트리(BST)의 정렬된 순서로 탐색
→ 검색, 데이터 정렬, 수식 계산 및 파싱 (수학적 표현식 변환)
③ 후위 순회 (Postorder Traversal): 왼쪽 → 오른쪽 → 루트 (LRV)
👉 D → E → B → F → G → C → A
(1) 왼쪽 자식을 방문
(2) 오른쪽 자식을 방문
(3) 자기 자신을 처리
자식 노드를 모두 처리한 후에 부모 노드를 방문하는 방식
→ 파일 삭제(하위부터), 컴파일러
④ 레벨 순회 (Levelorder Traversal): 루트부터 레벨별로 왼쪽에서 오른쪽으로 (BFS, 너비 우선 탐색)
👉 A → B → C → D → E → F → G
(1) 현재 레벨의 모든 노드를 처리
(2) 왼쪽 자식을 방문
(3) 오른쪽 자식을 방문
너비 우선 탐색(BFS) 방식(트리를 위에서 아래로, 왼쪽에서 오른쪽으로 탐색)
→ 최단 경로 탐색, AI 탐색 알고리즘(예: 체스, 길찾기), 네트워크
📌 3. 이진트리의 종류
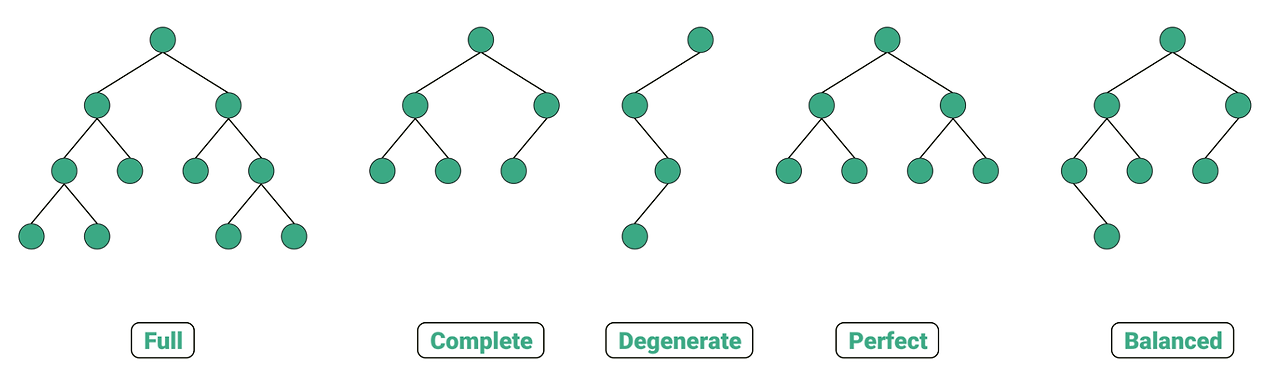
① 포화 이진 트리 (Full Binary Tree)
모든 노드가 자식 2개 또는 0개를 가짐.
모든 레벨이 꽉 차 있지는 않아도 됨.
② 완전 이진 트리 (Complete Binary Tree)
마지막 레벨을 제외한 모든 노드가 가득 차 있으며, 마지막 레벨의 노드는 왼쪽부터 순서대로 채워짐.
힙(Heap) 자료구조에서 많이 사용됨.
③ 퇴화 이진 트리 (Degenerate Binary Tree)
모든 노드가 자식 노드를 하나만 가짐.
연결 리스트(Linked List)와 유사한 구조로, 탐색, 삽입, 삭제 연산이 O(n) 으로 증가.
④ 정 이진 트리 (Perfect Binary Tree)
모든 내부 노드는 자식 2개, 모든 리프 노드는 같은 깊이에 위치.
노드 개수는 항상 2^ℎ−1 형태.
⑤ 이진 탐색 트리 (Binary Search Tree, BST)
왼쪽 서브트리는 부모보다 작은 값, 오른쪽 서브트리는 부모보다 큰 값을 가짐.
평균적인 탐색, 삽입, 삭제 연산의 시간 복잡도는 O(log n), 최악의 경우 O(n).
4. 이진트리 구현(Java)
이진트리를 직접 구현해보자.
'50, 30, 70, 20, 40, 60, 80'의 값들을 이진 탐색 트리(BST)로 구현할 것이다.
결론적으로, 트리는 아래와 같이 만들어질 것이다.
50
/ \
30 70
/ \ / \
20 40 60 80
// 이진 트리의 노드 클래스 (각 노드가 값을 가지며 왼쪽/오른쪽 자식을 가짐)
class Node {
int value; // 노드의 값
Node left, right; // 왼쪽 자식 노드, 오른쪽 자식 노드
// 생성자 (새로운 노드를 만들 때 값만 설정하고, 자식 노드는 없음)
public Node(int value) {
this.value = value;
left = right = null;
}
}
// 이진 트리 클래스 (삽입 및 탐색 기능 포함)
class BinaryTree {
Node root; // 트리의 루트 노드 (초기에는 null)
// 이진 탐색 트리(BST) 방식으로 노드를 삽입하는 메서드
Node insert(Node root, int value) {
if (root == null) return new Node(value); // 루트가 없으면 새 노드를 생성하여 반환
// 삽입할 값이 현재 노드보다 작으면 왼쪽 서브트리에 삽입
if (value < root.value) {
root.left = insert(root.left, value);
}
// 삽입할 값이 현재 노드보다 크면 오른쪽 서브트리에 삽입
else {
root.right = insert(root.right, value);
}
return root; // 변경된 루트 반환
}
// 특정 값이 트리에 존재하는지 탐색하는 메서드
boolean search(Node root, int key) {
if (root == null) return false; // 루트가 null이면 존재하지 않음
if (root.value == key) return true; // 현재 노드의 값이 찾는 값과 같으면 true 반환
// 찾는 값이 현재 노드보다 작으면 왼쪽 서브트리에서 검색
if (key < root.value) {
return search(root.left, key);
}
// 찾는 값이 현재 노드보다 크면 오른쪽 서브트리에서 검색
else {
return search(root.right, key);
}
}
}
// 실행 클래스 (메인 메서드 포함)
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree(); // 이진 트리 객체 생성
// 노드 삽입 (이진 탐색 트리 구조 유지)
int[] values = {50, 30, 70, 20, 40, 60, 80};
for (int value : values) {
tree.root = tree.insert(tree.root, value);
}
// 값 탐색 테스트
int searchValue = 40;
if (tree.search(tree.root, searchValue)) {
System.out.println(searchValue + "을(를) 찾았습니다.");
} else {
System.out.println(searchValue + "이(가) 존재하지 않습니다.");
}
}
}
