[week01/03.18]TIL

하루 한 줄 요약

(오늘은 사진으로 요약해볼게요)

오늘 공부한 내용

• 재귀( vs 반복문, 8-Queen)
• 정렬 3회차
• 파이썬( sort() vs sorted(), remove() vs pop() vs del vs slice)

새로 배우게 된 내용

재귀

재귀 vs 반복문

반복문으로 구현한 피보나치 수열

def fibo_loop(N):
    num_list = [1, 1]  
    if N <= 2:
        return num_list[N - 1]  
    else:
        for i in range(2, N):
            num_list.append(num_list[i - 2] + num_list[i - 1])  
        return num_list[N - 1]  # Return the Nth Fibonacci number

print(fibo_loop(5))  # Output: 5

재귀로 구현한 피보나치 수열

def fibo_recursive(N):
    if N == 1 or N == 2:  # 기본 조건 (Base Case)
        return 1
    return fibo_recursive(N - 1) + fibo_recursive(N - 2)  # 재귀 호출

print(fibo_recursive(5))  # Output: 5

N-Queen

N = int(input())
count = 0
pos = [0] * N
flag_col = [False] * N
flag_diagonal_up = [False] * (2 * N - 1)
flag_diagonal_down = [False] * (2 * N - 1)

def put():
    global count
    count += 1

def solve(row):
    if row == N:  # 모든 행에 대해 퀸을 놓았으면 카운트 증가
        put()
        return
    
    for col in range(N):
        if not flag_col[col] and not flag_diagonal_up[row + col] and not flag_diagonal_down[row - col + (N - 1)]:
            pos[row] = col
            flag_col[col] = flag_diagonal_up[row + col] = flag_diagonal_down[row - col + (N - 1)] = True
            solve(row + 1)  # 다음 행으로 이동
            flag_col[col] = flag_diagonal_up[row + col] = flag_diagonal_down[row - col + (N - 1)] = False  # 백트래킹

solve(0)
print(count)

퀸을 서로 공격할 수 없는 위치에 놓는 방법을 찾는 알고리즘.
퀸은 같은 행, 같은 열, 대각선↗️, 대각선↘️ 에 있는 말을 공격할 수 있다.

따라서 매 열에 퀸을 놓을때마다 행, 열, 대각선 두개를 확인해야한다

• 재귀 키워드는 어디서 나오는가?
  이 경우 앞에서 볼 수 있듯이 1열의 각 행을 돌면서 퀸을 놓아보고,
  1열의 정보를 기준으로 2열에 퀸을 두게 된다.
  또한 1열과 2열의 정보를 기준으로 3열의 각 행을 돌면서 퀸을 놓는 자리를 찾는다.

1열의 각 행을 돌면서 퀸을 놓아보고 => set(1)
1열의 정보를 기준으로 2열에 퀸을 두게 된다 => set(2)
또한 1열과 2열의 정보를 기준으로 3열에 퀸을 둔다 => set(3)

즉 set(i) 를 진행하면 재귀적으로 set(i + 1)을 진행하는 것!

• 같은 행, 같은 열, 같은 대각선 체크는 어떻게 할까?
  

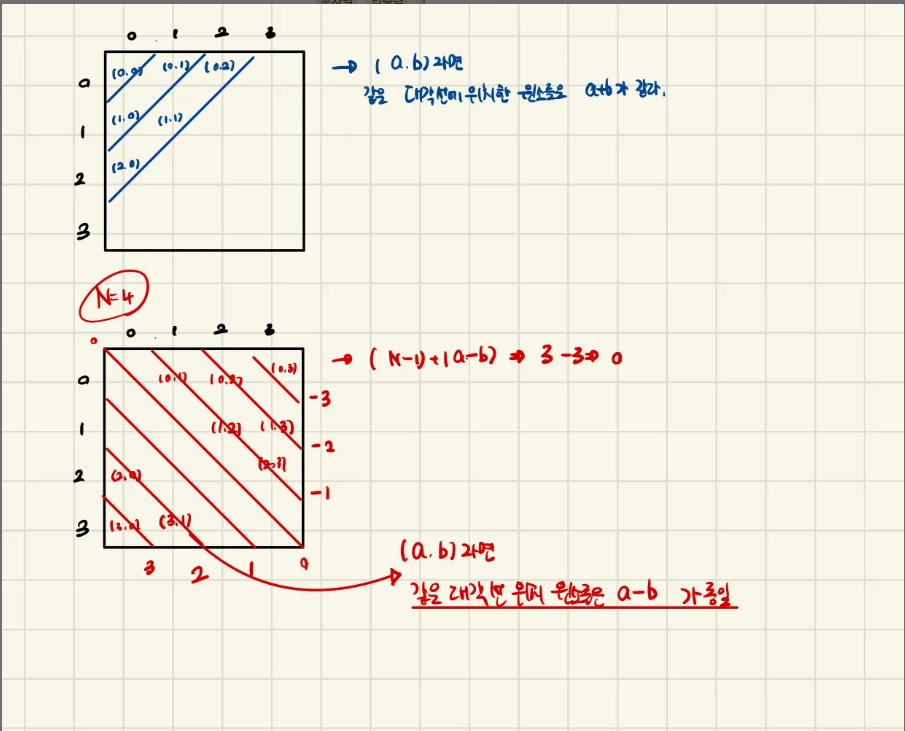
같은 행, 열은 어떻게 잘 이해했는데 같은 대각선에 있는 퀸을 판정하는 부분이 이해가 안가서
그림을 그려서 이해했다.

아직 60% 밖에 이해가 안된 것 같아서 내일 한번 더 살펴볼 예정.

파이썬 각종 비교

sort() vs sorted()

• sort() ⇒ 리스트형의 메소드(리스트 원본 값을 직접 수정), 따라서 반환값이 없다
• sorted() ⇒ 내장 함수, 리스트 원본 값은 보존, 정렬 값을 반환

remove() vs pop() vs del vs slice

• remove() ⇒ 지우고자 하는 값을 입력
  • 지우려는 값이 리스트 안에 2개 이상이면 앞에서 하나 지움

a = [1, 2, 1, 3, 4, 5, 1]
a.remove(1)

print(a)
print(a[0]) 
==============
[2, 1, 3, 4, 5, 1]
2

• pop(), del
  • 지우고자 하는 인덱스를 입력
  • del 은 반환값이 없고 리스트의 범위 지정이 가능

a = [1, 2, 1, 3, 4, 5, 1]
pop_return = a.pop(1)

print(a) # [1, 1, 3, 4, 5, 1]

a = [1,2,1,3,4,5,1] 
del a[1]
print(a) # #[1, 1, 3, 4, 5, 1] 

a = [1,2,1,3,4,5,1]
del a[:2]
print(a) # [1, 3, 4, 5, 1]

• slice
  • 사용자가 원하는 범위를 출력
  • 원본 리스트 그대로 존재
  • 원하고자 하는 범위 만큼 출력위해 새로운 리스트를 생성

그리고 광기의 7중 for문

https://www.acmicpc.net/problem/2309

heights = [int(input()) for _ in range(9)]
for i in range(9):
   for j in range(i+1, 9):
       for k in range(j+1, 9):
           for l in range(k+1, 9):
               for m in range(l+1, 9):
                   for n in range(m+1, 9):
                       for o in range(n+1, 9):
                           if heights[i] + heights[j] + heights[k] + heights[l] + heights[m] + heights[n] + heights[o] == 100:
                               result = [heights[i], heights[j], heights[k], heights[l], heights[m], heights[n], heights[o]]
                               result.sort()
                               for h in result:
                                   print(h)
                               exit()  # 정답 찾았으면 종료

9명의 난쟁이중 7명의 난쟁이를 뽑는 부분을 7중 for문으로 구현했다.
시간 초과가 나지 않겠다고 생각한 이유는 일단 시간 제한이 2초였다.

${}_9P_7$ 만큼 연산을 진행할 텐데 이게 18만 회 정도밖에 안나와서
다른 문제 풀다가 광기어린 눈으로 풀었다...^^
(근데 들여쓰기 때문에 시간 꽤 쓴건 함정)

공부하면서 어려웠던 점

일단 N-Queen 의 이론은 이해한 것 같은데 이걸 코드로 구현하는 과정
또한 재귀를 진행하는 과정에서 어떻게 문제를 풀어야 하는지가 와닿지가 않는다.

이럴땐 2회독, 3회독이지....