[자료구조] 개발자 필수 자료구조 7가지

FE.1·2023년 11월 6일

자료구조

선형 자료구조

한 개의 데이터 뒤에 다른 한 개의 데이터가 따라오는 구조
각 데이터들은 1:1의 구조를 가지고 있다.
배열, 리스트, 스택, 큐

배열(Array)

연속적인 메모리 공간에 데이터를 저장한다.
배열의 크기는 생성 시에 정해지며, 불변이다.
임의 접근(Random Access)이 가능하다.
- 인덱스를 통해 빠른 접근이 가능하다. $O(1)$
배열의 크기가 고정되어 있어 배열을 확장하려면 새로운 배열을 생성하고 기존의 데이터를 복사해야 한다.
예를 들어, 주식 차트에 대한 데이터는 중간에 데이터를 새롭게 추가하거나 삭제되는 정보가 아니며, 날짜별 주식 가격을 차례대로 저장해야 하는 데이터라서 순서를 보장해주는 자료구조인 배열을 사용하는 것이 좋다.

리스트(List)

연속적이지 않은 메모리 공간에 데이터를 저장한다.
크기가 동적이다.
리스트는 크게 배열 기반의 ArrayList와 연결 리스트 기반의 LinkedList로 구분된다.
데이터의 추가, 삭제가 배열에 비해 유연하지만, 특정 인덱스의 데이터에 접근하기 위해서는 처음부터 순차적으로 탐색해야 할 수도 있어 접근 속도가 느리다.
- ArrayList와 LinkedList로 구분한 것이 아닌, 일반화하여 설명한 리스트이니 혼동되지 말자!

ArrayList

내부적으로 데이터를 배열로 관리한다.
- 따라서 임의 접근(Random Access)이 가능하여 인덱스를 통한 데이터 접근이 빠르다.
데이터의 추가 또는 삭제 작업은 기존의 위치한 데이터들의 이동이 발생하여 상대적으로 느리다.
배열과 다르게 동적으로 크기를 조절할 수 있다. (동적 할당)
- 리사이징 - 내부적으로 가지고 있던 용량이 꽉 찼을 때, 기존의 용량 1.5배를 늘린 새로운 배열에 기존 배열을 Copy한다.

LinkedList(연결 리스트)

데이터가 노드(Node)형태로 저장되며, 각 노드는 다음 노드를 가리키는 참조(주소)를 가진다.
데이터의 추가 또는 삭제 작업이 빠르다.
- 해당 데이터의 포인터를 이전과 이후 데이터에 연결만 하면 된다.
특정 데이터에 접근하기 위해서는 Head노드부터 순차적으로 탐색해야 하므로 접근 속도가 느리다.
각 노드가 다음 노드의 참조(주소)를 변수(Point)에 저장해야 하기 때문에 추가적인 메모리 공간이 필요하다.

LinkedList 종류

1. 단방향 연결 리스트

다음 노드를 가리키기 위한 포인터만 가지고 있는 연결 리스트
현재 요소에서 이전 요소로 접근해야 할 때 부적합하다. → 이를 극복한 것이 양방향 연결 리스트

2. 양방향 연결 리스트

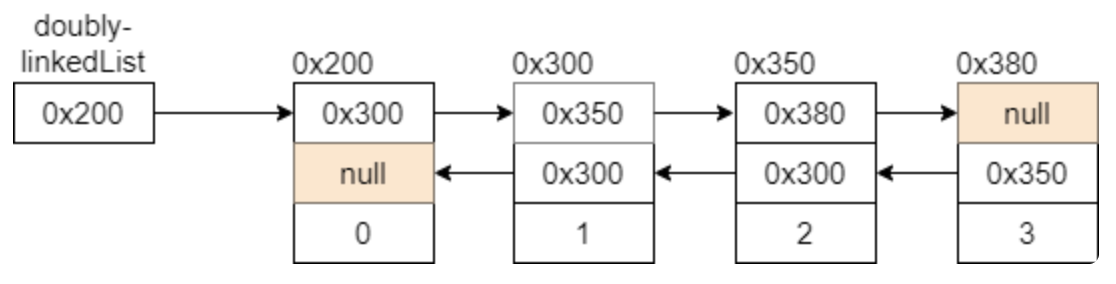
기존의 단일 연결 노드 객체에서 이전 노드 주소를 추가로 가지고 있는 연결 리스트
Java의 컬렉션 프레임워크에 구현된 LinkedList 클래스는 양방향 연결 리스트로 구현 되어 있다.

3. 양방향 원형 연결 리스트

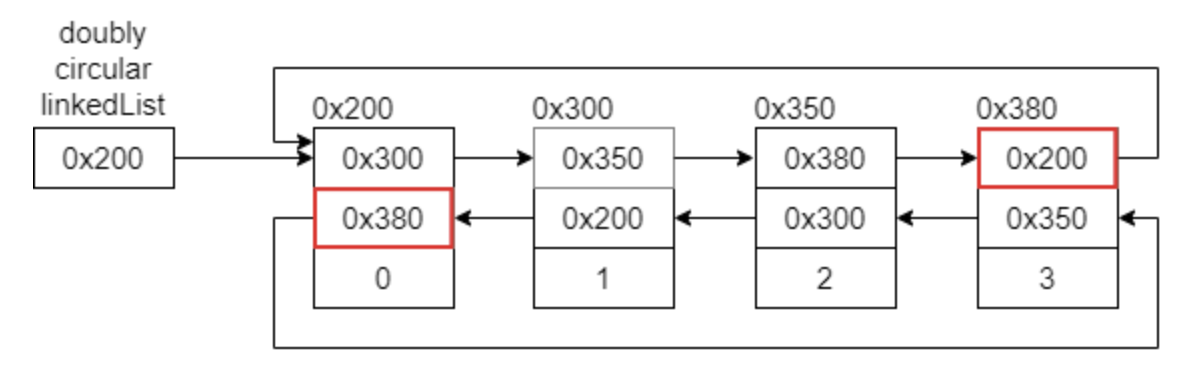
양방향 연결 리스트의 접근성을 개선한 연결 리스트
첫 번째 노드와 마지막 노드를 각각 연결시켜, 마치 원형 리스트 처럼 만든 연결 리스트
Tv 채널을 순회하거나 오디오 플레이어와 같이 데이터를 순차적 방식으로 처리하다 마지막 요소를 만나면 다시 처음 요소로 되돌아가는 상황에 사용된다고 보면 된다.

스택(Stack)

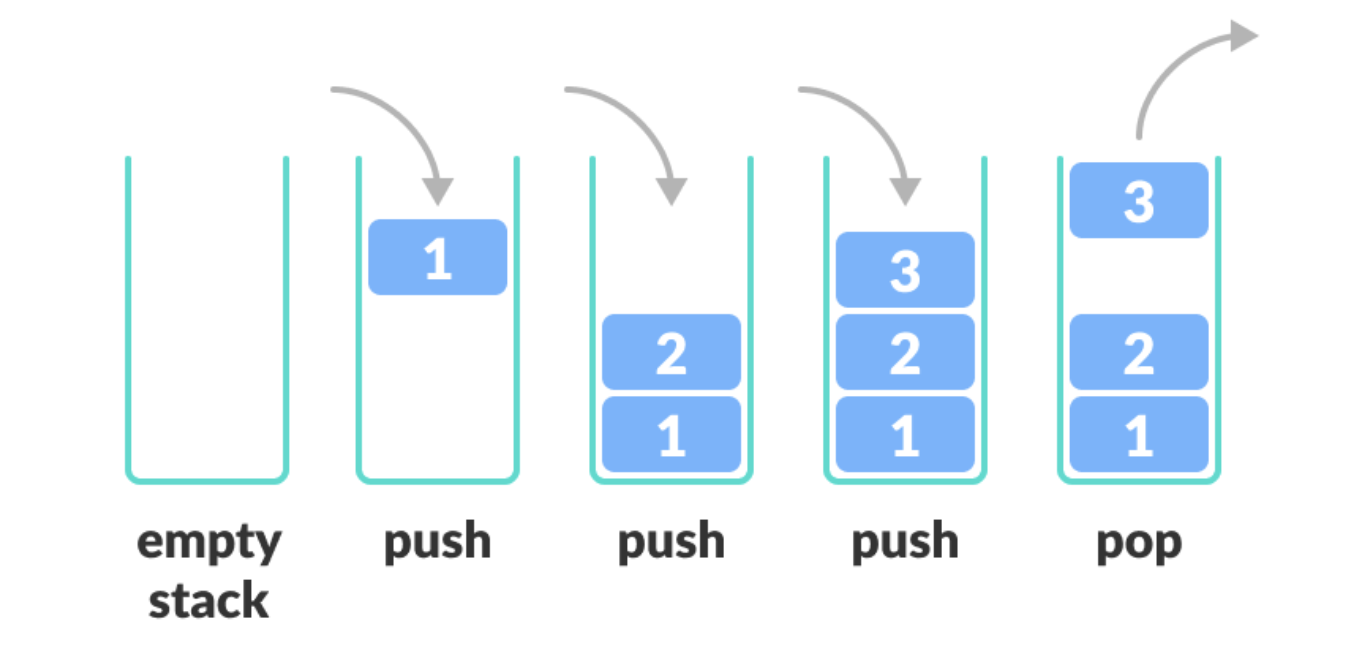
LIFO(Last In First Out) 구조
- 마지막에 들어온 데이터를 가장 먼저 꺼내게 되는 구조
데이터를 뒤에서부터 꺼내기 때문에 기존의 위치한 데이터들을 이동할 필요가 없으니 리스트보다는 배열로 구현하는게 좋다.
수식계산, 수식 괄호 검사, undo/redo, 웹 브라우저 히스토리, JVM Stack 메모리 등에서 스택이 사용된다.
자바의 Stack은 Vector 클래스를 상속받아 Thread-Safe하다는 특징이 있다.

[JAVA] Vector?

List 인터페이스를 상속받는 컬렉션 프레임워크의 일종
컬렉션 프레임워크가 나오기 전에 가변 개수의 배열이 필요할 때 사용했지만, 현대에는 성능 상 사용하지 않고 ArrayList를 사용한다.
- 따라서 ArrayList와 메서드 구성도 거의 같다.
멀티 스레드 환경에서의 Vector의 동기화
- ArrayList와의 차이점은 메서드에 synchronized 키워드의 유무이다.
- 따라서 Vector 클래스는 Thread-Safe하다는 특징이 있다.

💡 synchronized 키워드

멀티 스레드 환경에서 두 개 이상의 스레드가 하나의 변수에 동시에 접근할 때 Race condition(경쟁상태)이 발생하지 않도록 잠금을 거는 것

큐(Queue)

FIFO(First In First Out) 구조
- 먼저 들어간 데이터를 가장 먼저 꺼내는 구조
요소의 추가 및 삭제 작업 시 기존의 위치한 데이터들의 이동이 발생하므로 배열보다 연결 리스트로 구현하는게 좋다.
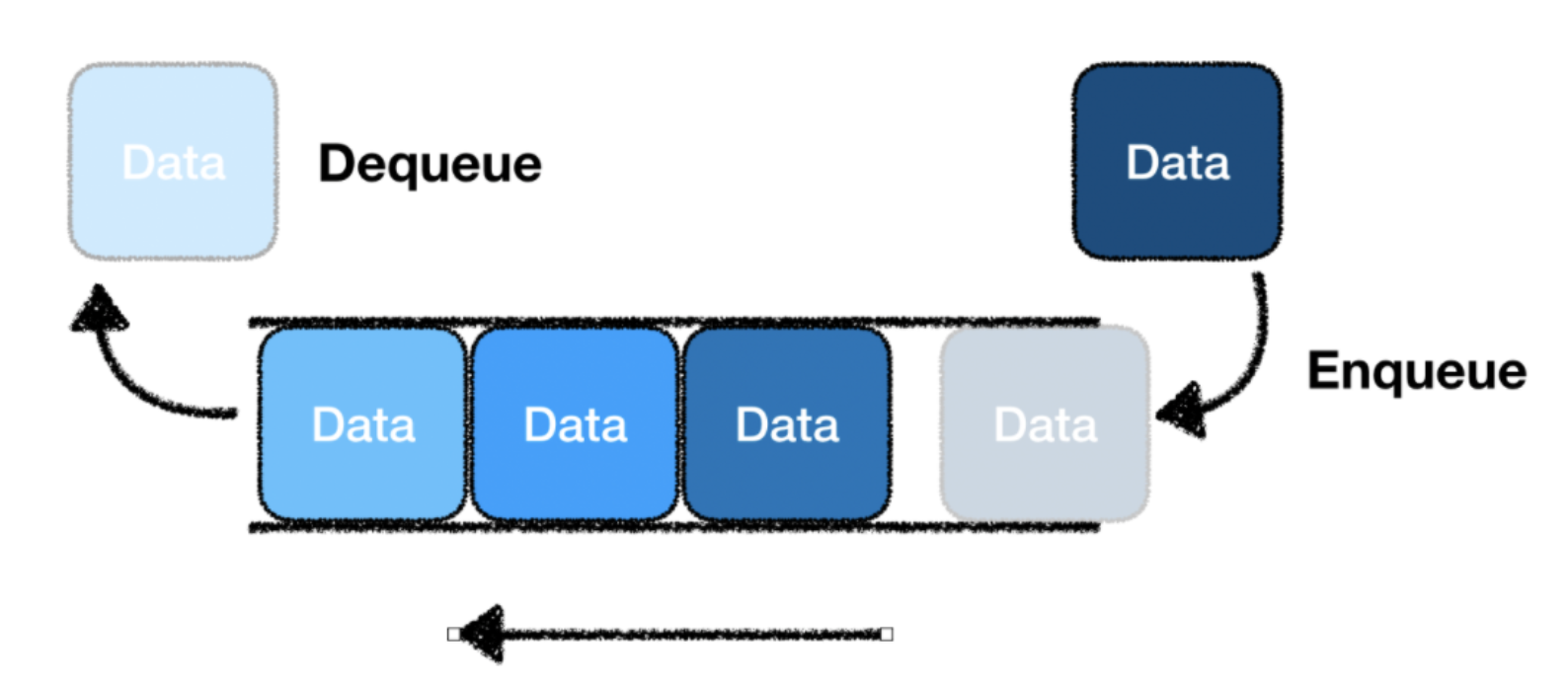
데이터가 들어가는 것을 Enqueue, 데이터가 나가는 것을 Dequeue라고 부른다.
- 큐의 한 쪽 끝은 front로 정하여 삭제 연산만 수행하고, 다른 한 쪽은 rear로 정하여 삽입 연산만 수행한다.
자바에서 큐는 이중 연결 리스트로 구현되어 있는 LinkedList 클래스로 초기화 한다.
그래프의 넓이 우선 탐색(BFS), 스케줄링 알고리즘 중 하나인 FCFS(First Come First Served)에서 큐가 사용된다.

순환 큐(환형 큐)

선형 큐의 오버플로우 문제를 해결하기 위한 방법 중 하나로, 배열의 끝과 시작이 연결된 형태로 구현된다.
자바의 표준 라이브러리에서는 순환 큐를 구현한 클래스를 제공하지 않는다.
1. 배열을 통해 직접 구현해야 한다.
2. ArrayDeque 클래스가 내부적으로 순환 구조를 사용하여 덱을 구현하므로, 크기가 고정되지 않은 순환 큐의 대안으로 사용할 수 있다.

우선순위 큐(Priority Queue)

들어간 순서에 상관없이 우선순위가 높은 데이터를 먼저 꺼내기 위해 고안된 자료구조
구현 방식에는 배열, 연결 리스트, 힙이 있고, 그 중 힙 방식은 최악의 경우 시간 복잡도 $O(logN)$ 을 보장하기 때문에 일반적으로 완전 이진트리 형태의 힙을 이용해 구현한다.
- 자바의 우선순위 큐는 힙 구조로 설계되어 있다.
- 자바는 PriorityQueue 클래스를 통해 우선순위 큐를 제공한다.
- 원소를 추가하거나 제거할 때 자동으로 정렬이 된다.

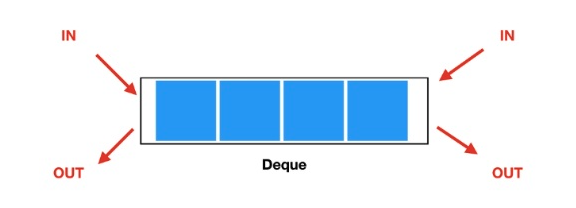
덱(Deque)

양쪽 끝에서 삽입과 삭제가 가능한 형태의 큐
자바에서 Deque 인터페이스의 구현체인 ArrayDeque 클래스를 사용하여 덱을 구현할 수 있다.
자바의 LinkedList도 Deque 인터페이스의 구현체이므로 덱을 구현할 수 있다.
- 양쪽 끝에서의 추가와 삭제 작업이 빈번하고, 중간 요소의 접근이 드물거나 없는 경우 ArrayDeque가 더 효율적이다.
- 만약 중간 요소에 대한 삽입, 삭제 작업이 자주 발생하고, 리스트를 순회하는 경우가 많다면 LinkedList가 더 적합할 수 있다.

비선형 자료구조

한 개의 데이터 뒤에 여러 개의 데이터가 따라오는 구조
각 데이터가 1:N 또는 N:N의 구조를 가지고 있다.
계층 구조를 표현하기에 적절한 자료구조로 트리와 그래프가 대표적인 비선형 자료구조이다.

트리(Tree)

노드(Node)와 노드를 연결하는 엣지(Edge)로 구성된 계층적인 자료구조
하나의 루트 노드에서 출발하여 여러 개의 자식 노드를 가질 수 있으며, 각 노드는 다른 자신의 자식 노드를 가질 수 있다.
파일 시스템, 데이터베이스의 인덱싱, DOM 구조 등에서 트리 구조가 사용된다.

트리 관련 용어

루트 노드: 부모가 없는 최상위 노드
단말 노드: 자식이 없는 노드
크기: 트리에 포함된 모든 노드의 개수
깊이: 루트 노드부터의 거리
높이: 깊이 중 최댓값
차수: 각 노드의 간선 개수(=각 노드의 자식 개수)

💡 기본적으로 트리의 크기가 N일 때, 전체 간선의 개수는 N-1개이다.

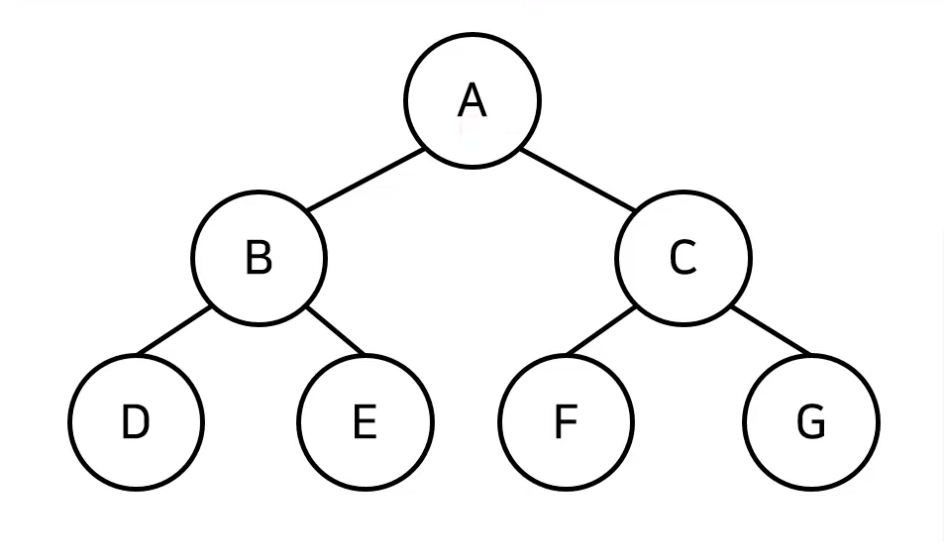
트리의 순회

트리의 포함된 노드를 한 번씩 방문하는 방법을 의미한다.
- 전위 순회: 루트를 먼저 방문한다.
  - A → B → D → E → C → F → G
- 중위 순회: 왼쪽 자식을 방문한 뒤에 루트를 방문한다.
  - D → B → E → F → C → G → A
- 후위 순회: 오른쪽 자식을 방문한 뒤에 루트를 방문한다.
  - D → E → B → F → G → C → A

이진 트리(Binary Tree)

각 노드가 최대 두 개의 자식 노드를 가지는 형태의 트리
특정한 순서를 따르지 않고, 노드의 배치가 자유롭다.
- 순서를 따르지 않기 때문에 탐색 속도가 이진 탐색 트리에 비해 느릴 수 있다.
힙은 완전 이진 트리의 일종으로, 완전 이진 트리는 부모 노드 밑에 자식 노드가 최대 2개까지 있을 수 있고, 마지막 높이를 제외한 모든 높이에 노드가 완전히 채워져 있는 트리 구조를 말한다.
- 힙의 종류는 최대 힙과 최소 힙이 있다.

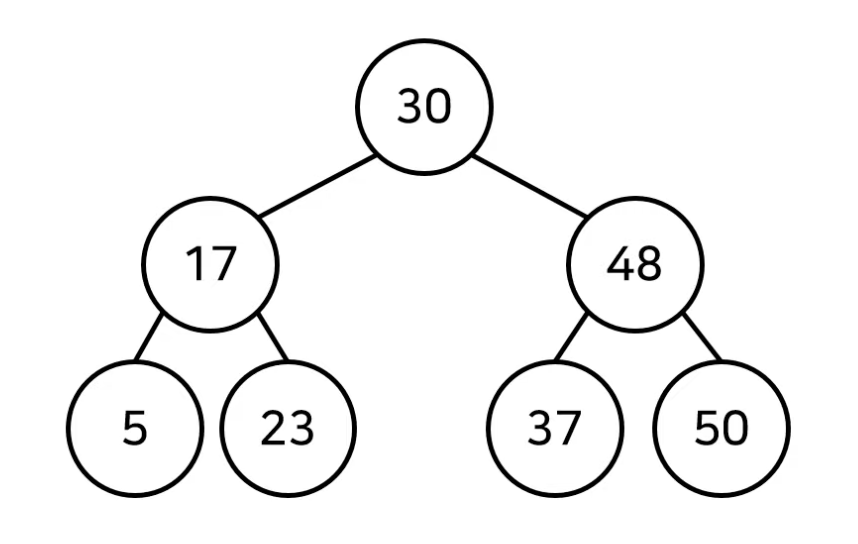
이진 탐색 트리(Binary Search Tree, BST)

이진 트리의 한 종류로, 이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조
모든 노드는 왼쪽 자식 노드보다 큰 값, 오른쪽 자식 노드보다 작은 값을 가지는 특징이 있다.
- 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
탐색, 삽입, 삭제 등의 연산을 $O(logN)$ 시간에 수행할 수 있어, 대량의 데이터를 효율적으로 관리할 수 있다.
정렬이 되어있는 경우, 효율적인 탐색이 가능하다.
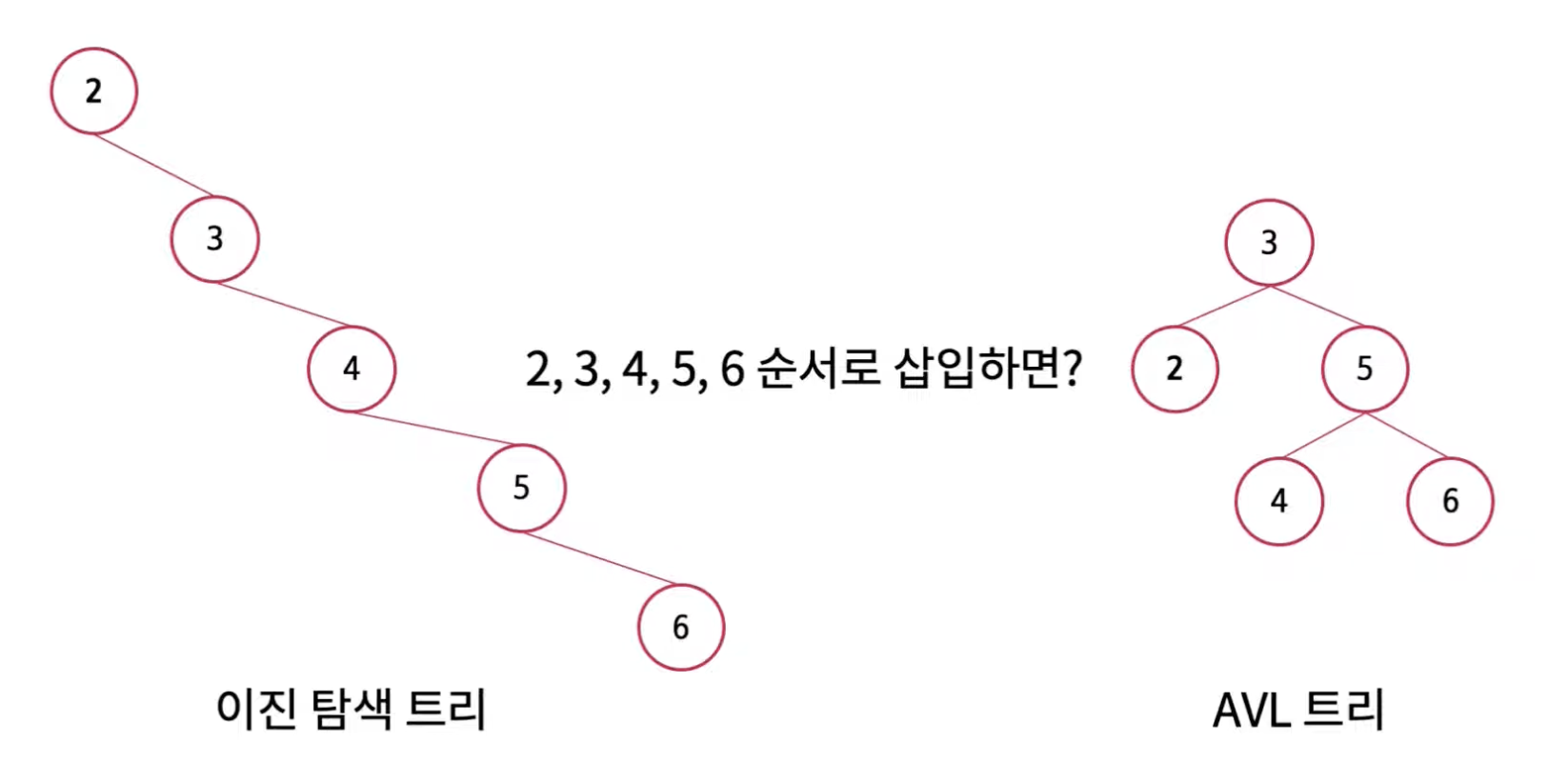
만약 트리의 균형이 한쪽으로 치우쳐진 경우, 최악의 경우 $O(N)$ 시간 복잡도를 갖게 되고, 이러한 문제(균형)를 개선하기 위해 나온 기법이 레드-블랙 트리(RBT), AVL 트리이다.

레드-블랙 트리(Red-Black Tree, RBT)

이진 탐색 트리(BST) 기반으로 하는 트리 자료구조
BST의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제점을 해결하기 위해 만들어졌다.
- 삽입과 삭제 연산 후에도 트리의 균형을 재조정하여 탐색 효율성을 보장한다.

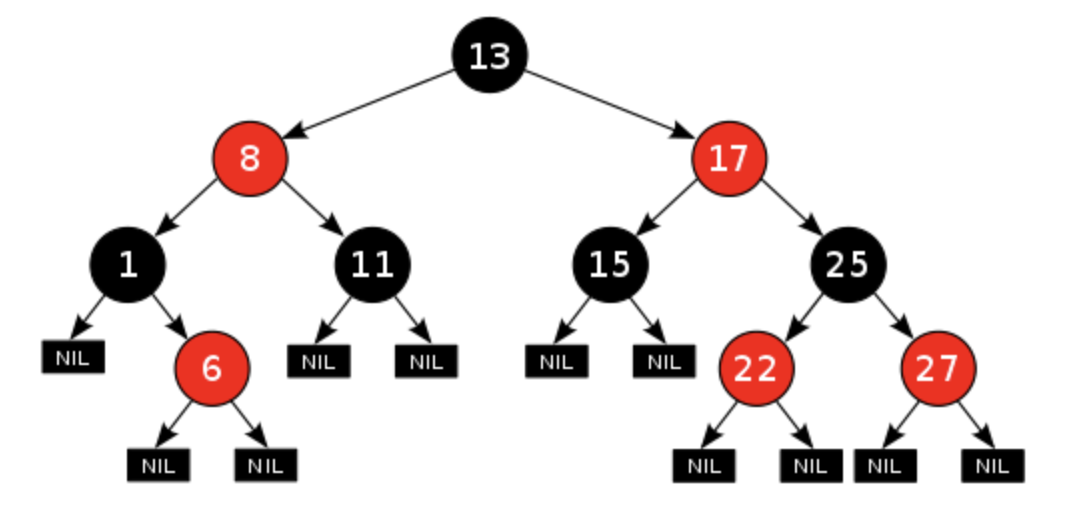
레드-블랙 트리의 규칙

모든 노드는 레드 or 블랙이다.
루트 노드(Root Node)는 블랙이다.
말단 노드(Leaf Node, NIL)는 블랙이다.
레드 노드의 자식 노드의 색은 블랙이다. (블랙 노드의 자식의 색은 상관없다.)
루트 혹은 특정 노드에서 말단 노드사이에 있는 블랙 노드의 개수는 같다.

레드-블랙 트리의 회전 방법은 링크 참고! [래드-블랙 트리 참고]

AVL 트리

이진 탐색 트리의 단점을 개선한 스스로 균형을 잡는 트리
균형도라는 것을 이용하여 삽입 및 삭제 시 균형을 맞춘다.
- 레드-블랙 트리보다 더 엄격하게 균형을 잡는다.
균형도가 절대값 2미만이면 균형 트리이고, 2이상이면 불균형 트리이다.
균형도를 구하기 위해서는 먼저 높이를 구해야 한다.

AVL 트리의 높이 구하기

단말 노드의 높이는 항상 0이다.
자식 노드가 없을 경우, 즉 null인 경우 높이는 -1로 본다.
높이는 아래에서부터 올라가 계산한다.
- 자식들의 높이 중 최대값 + 1

AVL 트리의 균형도 구하기

부모 노드 균형도 = 좌측 노드 높이 - 우측 노드 높이
단말 노드의 균형도는 항상 0
자식 노드가 없을 경우, 즉 null인 경우 높이는 -1로 본다.
균형도 또한, 아래에서부터 올라가 계산한다.

균형 vs 불균형

균형도가 양수이면 좌측으로 치우친 트리이고, 음수이면 우측으로 치우친 트리이다.
삽입 및 삭제로 인해 트리의 균형도가 무너질 수 있으며, 좌측으로 치우친 것을 LL 문제(Left-Left)라고 하고, 우측으로 치우친 것은 RR 문제(Right-Right)라고 한다. 이외에도 같은 원리로 LR 문제, RL 문제도 있다.

4가지의 불균형 트리의 문제에 따른 각각의 회전 방법은 링크 참고! [AVL 트리 참고]

레드-블랙 트리 vs AVL 트리

삽입 및 삭제 시 재배치 가능성이 RBT에 비해 상대적으로 적기 때문에 RBT가 적합할 수 있다.
연산이 적고, 탐색이 많을 경우, AVL 트리가 적합하다.

그래프(Graph)

노드(정점, Vertex)와 노드를 연결하는 엣지(간선, Edge)로 구성된 자료구조
그래프는 방향성이 있는 방향 그래프와 방향성이 없는 무방향 그래프로 나뉜다.
그래프의 간선에는 가중치를 부여할 수 있고, 가중치를 부여한 그래프를 가중치 그래프라고 부르며, 보통 거리, 비용, 우선순위 등을 나타내는 데 사용된다.
차수는 한 노드에 인접한 간선의 수를 의미한다.
네트워크 시스템, 소셜 네트워크, 지도의 경로 탐색 등 다양한 분야에서 그래프를 사용한다.
대표적으로 인접 리스트와 인접 행렬로 그래프를 표현한다.

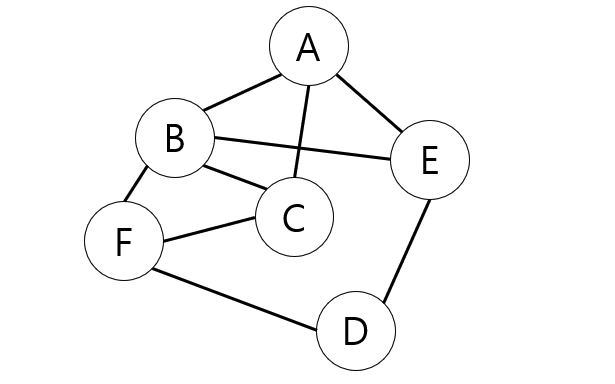
그래프의 장점

복잡한 관계를 직관적으로 표현할 수 있다.
다양한 최적화 문제를 풀 수 있다.
- 최단 경로 문제, 최소 신장 트리 문제 등

그래프의 단점

데이터의 규모가 커질수록 계산 비용이 증가한다.
방향성 그래프에서는 경로의 유무가 중요하므로, 경로가 존재하지 않는 경우에는 이를 고려하여 알고리즘을 설계해야 한다.
- 가중치를 조절하여 일정 이하의 가중치를 가진 간선들은 무시하는 방법으로 보완할 수 있다.

그래프의 탐색

깊이 우선 탐색(DFS, Depth-First Search)
- 한 방향으로 깊게 탐색하는 방식으로, 스택 또는 재귀를 사용한다.
너비 우선 탐색(BFS, Breadth-First Search)
- 같은 레벨에 있는 노드들을 우선 탐색하는 방식으로, 큐를 사용한다.

해시 테이블

키(Key)를 값(Value)에 매핑하는 구조를 가진 자료구조
F(key) → HashCode → Index → Value
해시 함수
- 키(Key)를 입력으로 받아서, 데이터가 저장될 배열의 인덱스를 계산한다.
- 해시 함수는 해시 테이블의 성능에 큰 영향을 미친다.
해시 코드
- 해시 함수에 의해 계산된 데이터의 위치를 나타내는 값이다.
버킷(Bucket) 또는 슬롯(Slot)
- 해시 코드에 해당하는 해시 테이블의 위치로, 실제 값이 저장되는 곳이다.
평균적으로 시간 복잡도 $O(1)$ 로 데이터를 빠르게 조회한다.
- 최악의 경우(모든 키가 같은 버킷으로 충돌하는 경우 등)에는 시간 복잡도 $O(N)$ 까지 떨어질 수 있다.

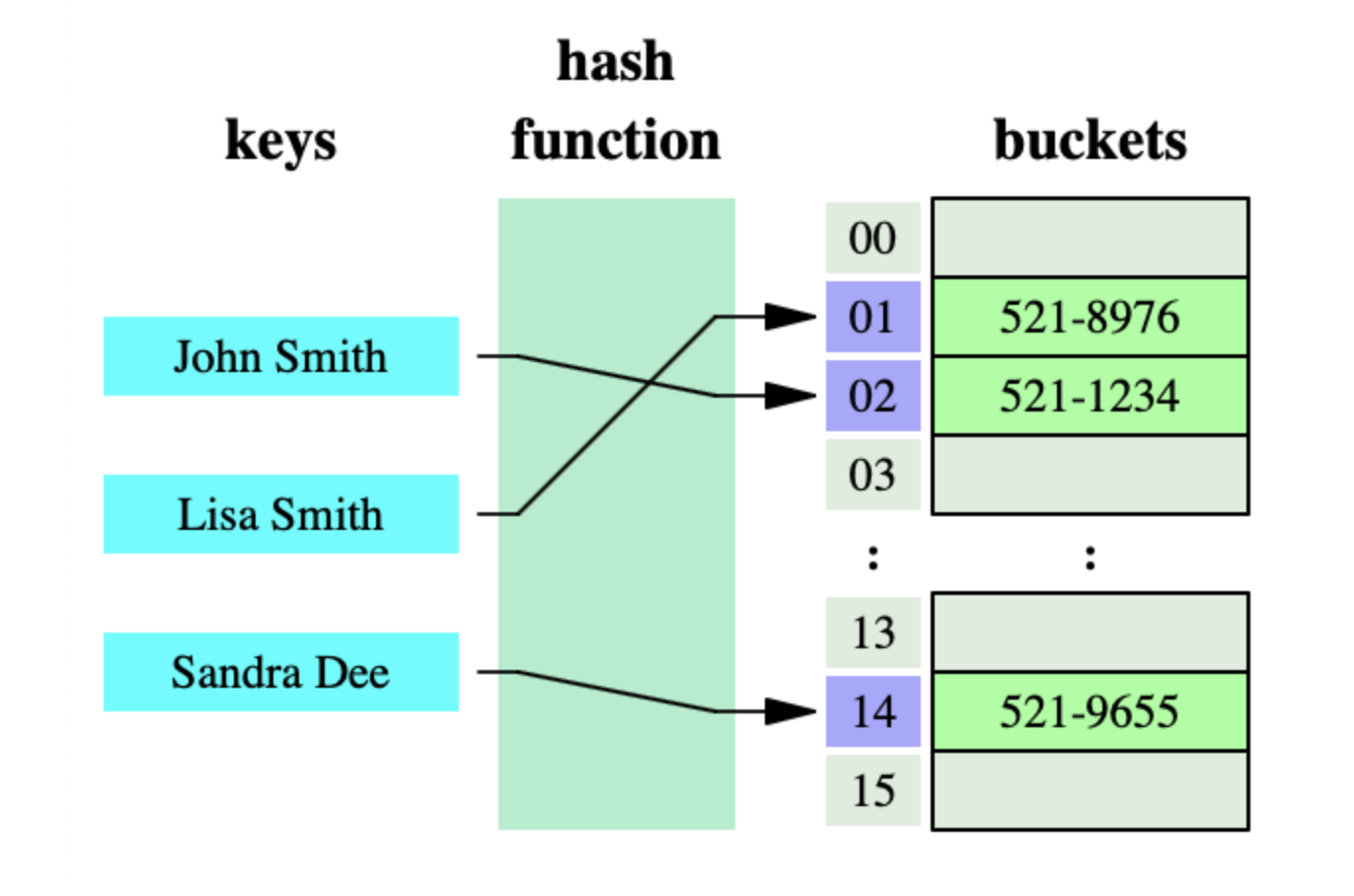
해시 충돌 해결 방법

두 개 이상의 키가 동일한 해시 코드를 가지면 충돌(Collision)이 발생한다.

1. 분리 연결법(Separate Chaining)

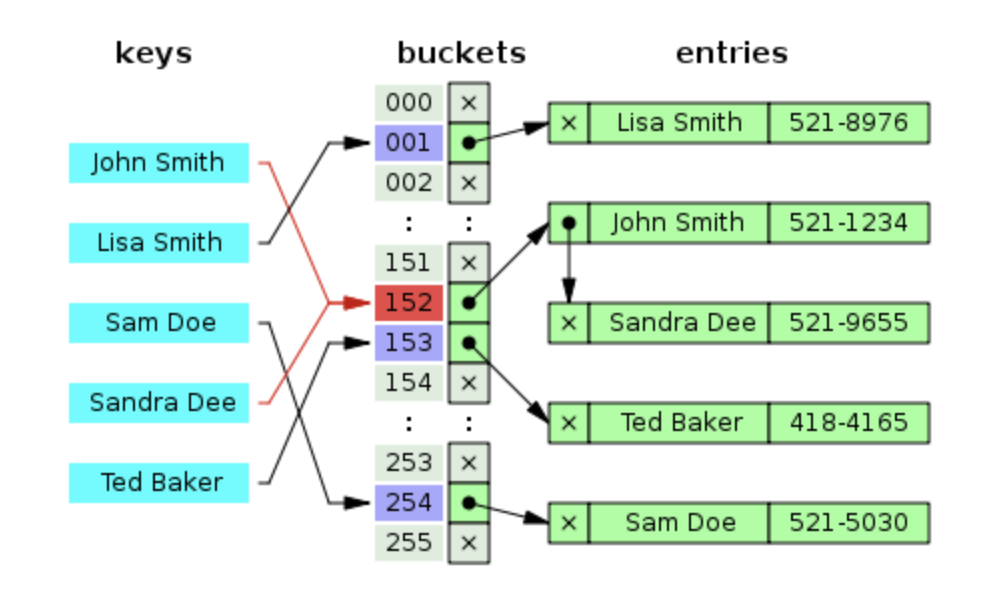
각 버킷에 연결 리스트 같은 자료구조를 사용하여, 같은 해시 코드를 가진 항목들을 연결한다.
Java8의 해시 테이블은 Self-Balancing Binary Search Tree 자료구조를 사용해 Chaining 방식을 구현한다.
이러한 Chaining 방식은 해시 테이블의 확장이 필요없고 간단하게 구현이 가능하며, 손쉽게 삭제할 수 있다는 장점이 있지만, 데이터의 수가 많아지면 동일한 버킷에 Chaining되는 데이터가 많아져 그에 따라 캐시의 효율성이 떨어진다는 단점이 있다.

2. 개방 주소법(Open Addressing)

추가적인 메모리를 사용하는 Chaining 방식과는 다르게 비어있는 해시 테이블의 공간을 활용하는 방법이다.

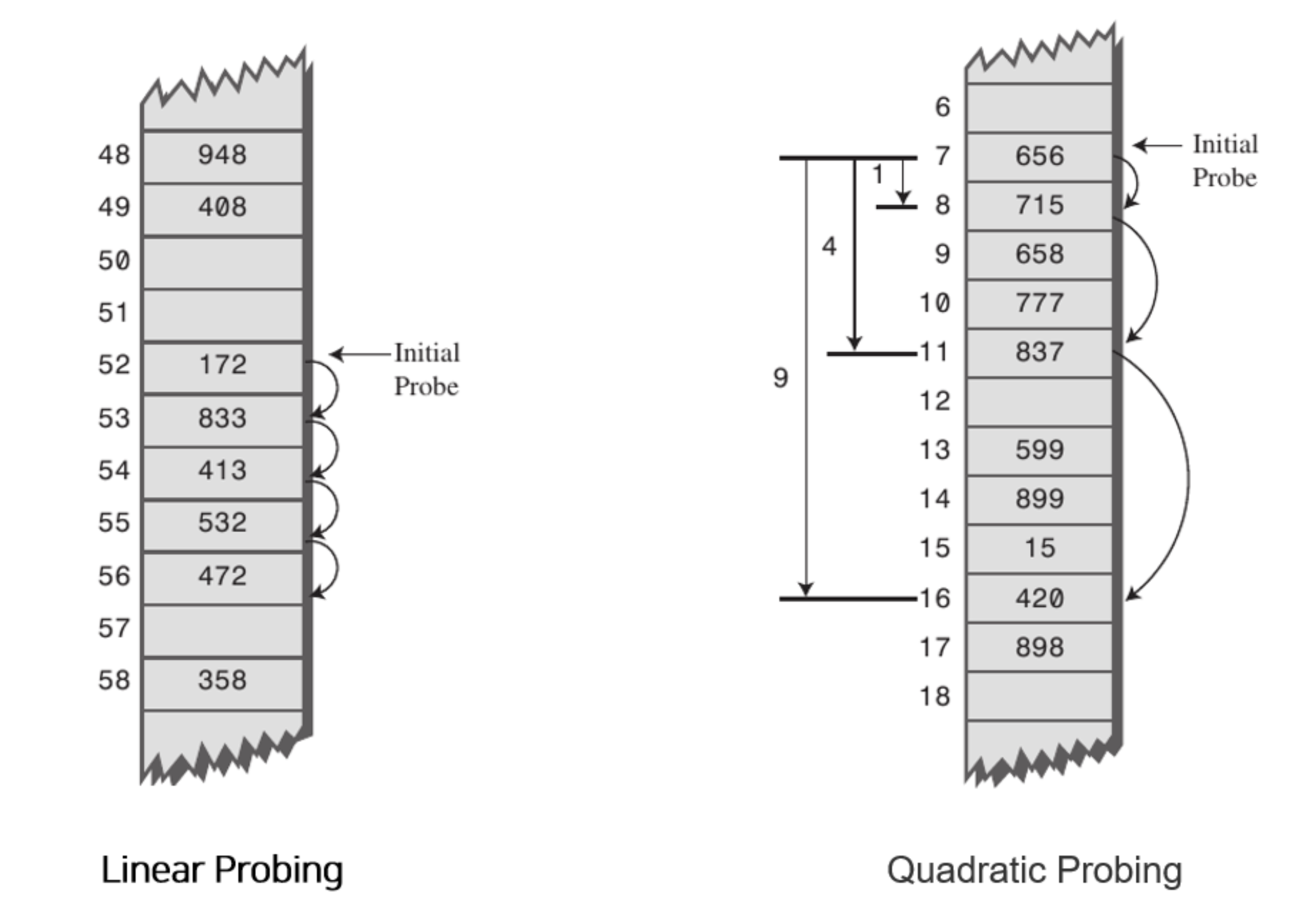
1. 선형 탐사(Linear Probing)

현재의 버킷 index로부터 고정폭 만큼씩 이동하여 차례대로 검색해 비어 있는 버킷에 데이터를 저장한다.

2. 이차 탐사(Quadratic Probing)

해시의 저장순서 폭을 제곱으로 저장하는 방식이다.

3. 이중 해싱(Double Hashing Probing)

해시된 값을 한번 더 해싱하여 해시의 규칙성을 없애버리는 방식이다.
해싱을 두 번 하기 때문에 다른 방법들보다 많은 연산을 하게 된다.
개방 주소법에서 데이터를 삭제하면 삭제된 공간은 Dummy Space로 활용되므로, 해시 테이블을 재정리 해주는 작업이 필요하다.

[참고1]
[참고2]
[참고3]
[참고4]

FE.1

공부하자!

이전 포스트

[JAVA] JDK, JRE, JVM?

다음 포스트