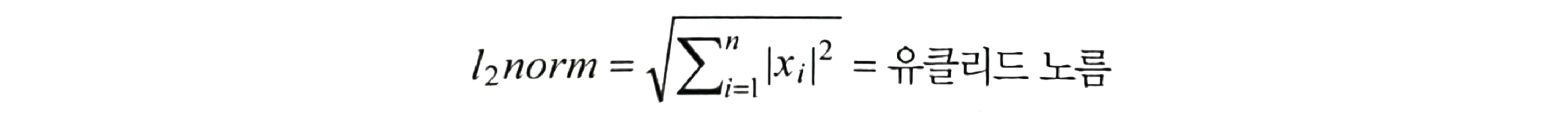딥러닝 5일차

4장

하드 컴퓨팅
<->
소프트 컴퓨팅

자동으로 계산해서 퍼포먼스를 한다.

Word2Vec 파라미터 정리

sentences : Word2Vec 모델 학습에 필요한 문장 데이터. Word2Vec 모델의 입력값으로 사용됩니다.
size :

신경망 구조를 할떄 입출력은 고정인데 한데 중간에 딥한 신경망을 만들때 노드를 몇개를 만들지는 자기 마음이다. 대부분 이렇게 이렇게 하라는 가이드가 있다. 딱 떨어지게 지시를 했으면 좋겠으나 그런 자유도가 있다.

한 개만 나오는 특별한 값은 사전을 늘리고 정확성을 떨어트려서 제거한다.

빅 데이터 이전 시대와 별 차이 없다.
데이터의 양이 많이 늘었을 뿐이다.

표본 자체가 적어도 빅데이터에서는 결과값에 영향을 미치지 않는다.

5장 텍스트 유사도

가장 유사한 답을 찾는다.
문장 간에 뜻이 얼마나 비슷한지를 계산할 수 있어야 한다.
의미상 같은 값이 얼마나 분포되어 있는가
겟 시뮬라리티를 이용하기도 한다./

문장 전체에 이용하면 좋겠다.

5.1 텍스트 유사도 개요

• 자연어 처리에서 문장 간 의미 유사도 계산은 중요

• 두 개의 문장에 동일한 단어나 의미상 비슷한 단어들이 얼마나 분포되어 있는가

• Q&A 챗봇

• 챗봇 엔진에 입력되는 문장과 시스템에서 해당 주제의 답변과 연관되어 있는 질문이 얼마나 유사한지 계산
• 문장 내 단어를 수치화

• 통계에 의한 방법(5장) vs. 인공 신경망에 의한 방법(Word2Vec)

인공 신경망으로 학습을 하고 입력되는 단어간의 유사도를 구하는 것이 Word2Vec
5장에서 배울 것은 통계에 의한 방법이다.

5.2 n-gram 유사도

n-gram

• 문장에서 n개의 연속적인 단어 시퀀스 -> 토큰
• 이웃한 단어의 출현 횟수를 통계적으로 표현하여 텍스트의 유사도 계산
• 손쉬운 구현 방식

단어들의 연속된 것들을 토큰화
통계적으로 표현 -> 텍스트의 유사도 계산

1 = 유니그램
2 = 바이그램
3 = 트리그램
4 = 포 그램

'사랑'을 저번에 만든 test 코드에서 어떻게 되는지 해설

사랑을 0000001000000이라고 값을 주었을때
이것을 가지고 긍정적인지 부정적인지를 표현해준다.
가중치를 조정함으로서 한다.
가중치가 결국에는 임베딩이 된다.

200 * 107에서 '사랑'과 유사한 것들을 찾는다. 그렇게 해서 가중치 조정을 해서 임베딩을 완성 찾아간다.

n-gram은 빈도 수를 가지고 계산한다.

그 차이가 있다.

n-gram은 토큰 하나하나를 비교하는게 아닌 옆의 단어까지 참고하여 얼마나 유사한지를 측정한다.

찾은 규칙이 우리가 원했던 패턴일 수 있고 전혀 그렇지 않은 패턴일 수 있다.

사랑이라는 단어가 맨 위에 0.37이렇게 나오는데 이것이 무엇을 의미하는지는 모르지만. 따뜻한 정도인지 아닌지를 모른다.

여러가지를 조합해서 따뜻함을 표현할 수도 있다.

많은 입력 데이터와 가중치 에러가 적게 되도록
각각에 대해서 해보니까 재밌게도 사랑하고 죽음 가까운 값으로 나온다.

자리가 부족하다.

너무 압축적이다

ex) 은행원이 적절히 적으면 고객들에 대한 일반적인 내용을 배울 수 있다.

새로운 고객이 오더라도 대응 할 수 있다.

그러나 특정 고객만을 처리하게 된다면 새로운 고객에 대응이 힘들 수 있다.

이러한 것을 과적합이라고 한다. 너무 학습을 많이 하거나 적게 할경우를 과적합이라고 한다.

은행원은 특정한 고객이 아닌 자기 선에서 많은 데이터들을 다루어 공통적인 패턴들을 공부하고 새로운 고객에 대해서도 공통적인 패턴을 적용한다. 그렇게 하여 새로운 고객을 한다.

만약 너무 학습량이 많으면 학습이 되지 않는다. 과소적합이라고 한다.

그래서 200개 정도가 괜찮다고 생각하여 200~300정도를 선택한다.

window 사이즈는 주변 단어 윈도우의 크기이다.

유사도 측면에서는 '뉴턴''6월'과 '6월''뉴턴'이 같다고 판단하는 것이 정확성이 높다.

n-gram을 이용한 문장 간 유사도 계산

• 단어 문서 행렬(TDM, Term-Document Matrix) 생성
• 동일한 단어의 출현 빈도를 확률로 계산
• tf(term frequency): 두 문장 A와 B에서 동일한 토큰의 출현 빈도
• tokens: 해당 문장에서 전체 토큰 수
• 토큰: n-gram으로 분리된 단어
• 기준이 되는 문장 A에서 나온 전체 토큰 중에서 A와 B에 동일한 토큰이 얼마나 있는지 비율
• 1.0에 가까울수록 B가 A에 유사하다

A: 6월에 뉴턴은 선생님의 제안으로 트리니티에 입학했다. B: 6월에 뉴턴은 선생님의 제안으로 대학에 입학했다.

마지막 입합은 잘못 된 것

제안 트리니티

B문장에서는 트리니티 대신에 '대학'을 썼다.

[예제 5-1] 2-gram 유사도 계산
n-gram 특징

• n을 크게 잡을수록 비교 문장의 토큰과 비교할 때 카운트를 놓칠 확률 높음
  -> 틀린 경우가 많이 생기기 때문에
• n을 작게 잡을수록 카운트 확률은 높아지지만 문맥을 파악하는 정확도는 떨어짐
  -> 각 단어에만 집중을 하기 때문
• n은 보통 1~5

• 어절 단위 n-gram vs. 음절 단위 n-gram

  어절 : 문장을 이루는 도막도막의 마디, 문장 성분의 최소단위로서 띄어쓰기의 단위가 된다.

  음절 : 음의 한 마디, 단어 또는 단어의 일부를 이루는 발음의 단위로, 단숨에 내는 모음과 자음이 어울린 한덩어리의 소리를 말한다.

  
  

코드

ch05.ipynb

from konlpy.tag import Komoran

꼬꼬마에 있는 것을 활용

# 어절 단위 n-gram
def word_ngram(bow, num_gram): # --> 함수 헤더, 함수 시그니처, interface
    #text = tuple(bow)
    #ngrams = [text[x:x + num_gram] for x in range(0, len(text))]
    if num_gram < 1:
        print('WARNING: num_gram must be greater than 1')
        return tuple()
    text = tuple(bow)
    ngrams = [text[x:x + num_gram] for x in range(0, len(text) - num_gram + 1)]
    
    return tuple(ngrams)
 

# 유사도 계산
def simularity(doc1, doc2):
    tf  = 0.0
    for token in doc1:
        if token in doc2:
            tf += 1       #tf
    
    return tf / len (doc1)

# 문장 정의
sentences = ['6월에 뉴턴은 선생님의 제안으로 트리니티에 입학했다.',
             '6월에 뉴턴은 선생님의 제안으로 대학교에 입학했다.',
             '나는 맛있는 밥을 뉴턴 선생님과 함께 먹었다.']

# 형태소 분석기에서 명사(단어) 추출
komoran = Komoran()

bows = [komoran.nouns(i) for i in sentences]
print(bows)

결과값

[['6월', '뉴턴', '선생님', '제안', '트리니티', '입학'], ['6월', '뉴턴', '선생님', '제안', '대학교', '입학'], ['밥', '뉴턴', '선생', '님과 함께']]

# 단어 n-gram 토큰 추출
docs = [word_ngram(bow,2) for bow in bows]
print(docs)

[(['6월', '뉴턴'], ['뉴턴', '선생님'], ['선생님', '제안'], ['제안', '트리니티'], ['트리니티', '입학']), (['6월', '뉴턴'], ['뉴턴', '선생님'], ['선생님', '제안'], ['제안', '대학교'], ['대학교', '입학']), (['밥', '뉴턴'], ['뉴턴', '선생'], ['선생', '님과 함께'])]                    

for n, doc in  enumerate(docs):
    print(f'{n}번 문서의 n-gram:\n {doc}\n')

5.3 코사인 유사도

• 두 벡터 간 코사인 각도를 이용해 유사도 측정
• 벡터의 크기가 중요하지 않을 때 주로 사용
• 두 벡터의 방향이 완전히 동일한 경우: 1
• 반대 방향: -1
• 직각: 0
• 두 벡터의 방향이 같아질수록 유사하다

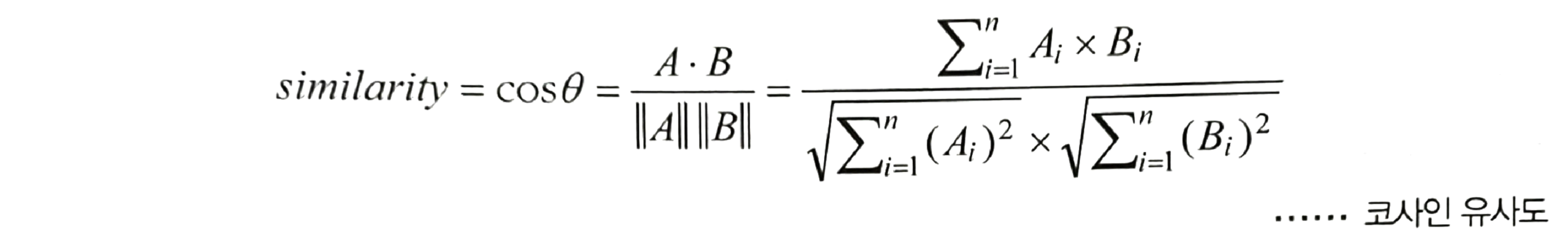
[예제 5-2] 코사인 유사도 계산