[백준/c++] 9663번 : n-Queen

문제링크

---

아이디어

n*n 크기의 체스판에 n개의 퀸을 서로 공격하지 못하는 위치에 배치할 수 있는 경우가 총 몇 개인지 출력하는 문제이다.

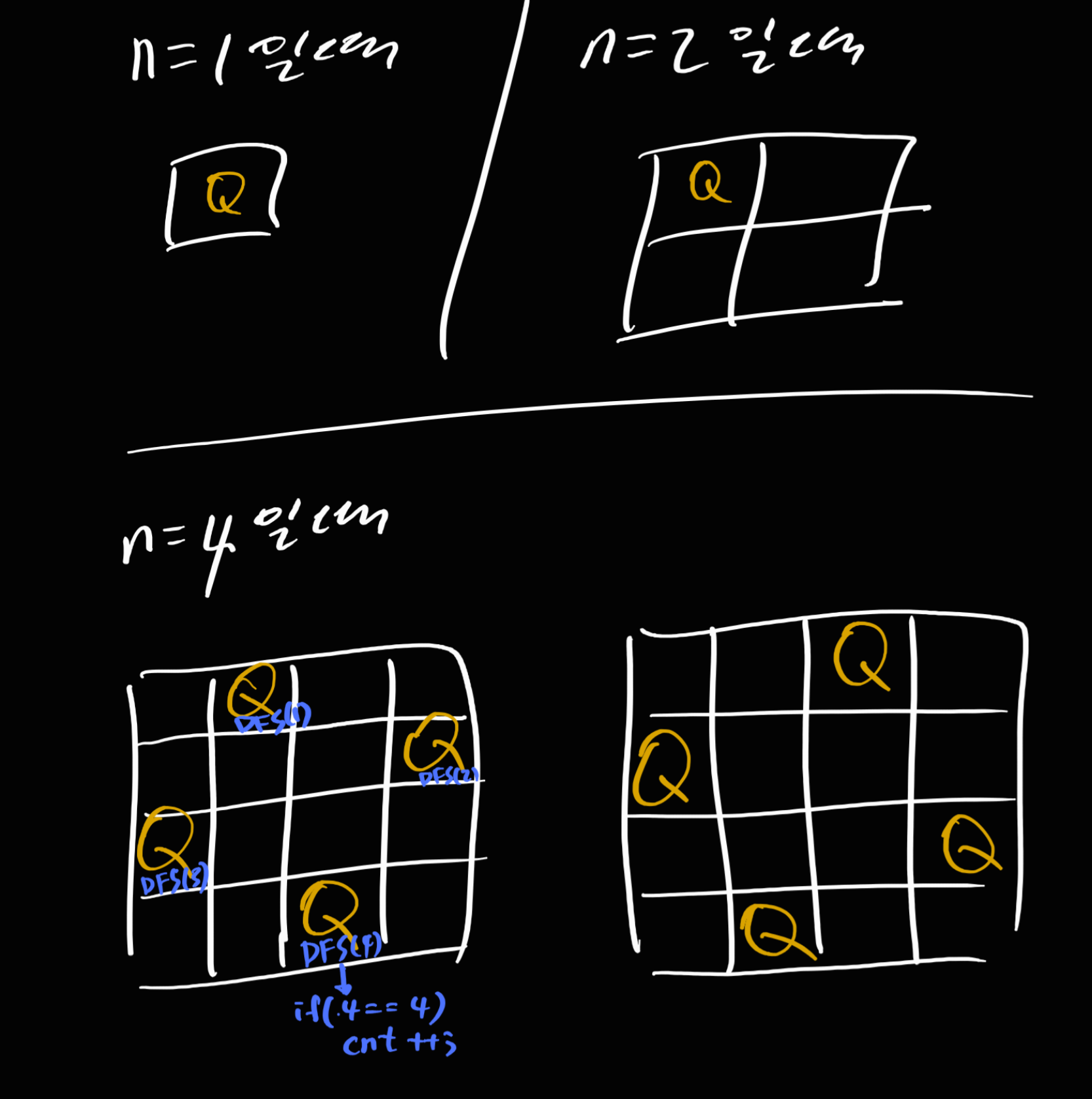
퀸은 한 행에 하나씩 밖에 놓지 못한다. 그 말은 행을 증가시켜 n까지 반복했
따라서 각 행에서 퀸을 놓을 수 있는 자리에 퀸을 놓자마자 행을 하나 증가시켜 그 다음 행에서 퀸을 놓을 자리를 찾는 것을 반복할 것이다.

n=4인 경우
먼저 퀸을 (0,0)에 놓았다고 하자. 즉, col[0] = 0이다. 현 위치에 배치 가능한지 Placeable을 호출시켜 이전 행들에 놓여진 퀸과 비교한다. 하지만 0번째 행이기 때문에 바로 true를 반환하고 DFS(i+1)을 호출해 행을 증가시켜준다.

1번째 행에서도 현재 위치가 놓을 수 있는 위치가 될 때까지 j를 증가시켜 위치를 갱신해준다.

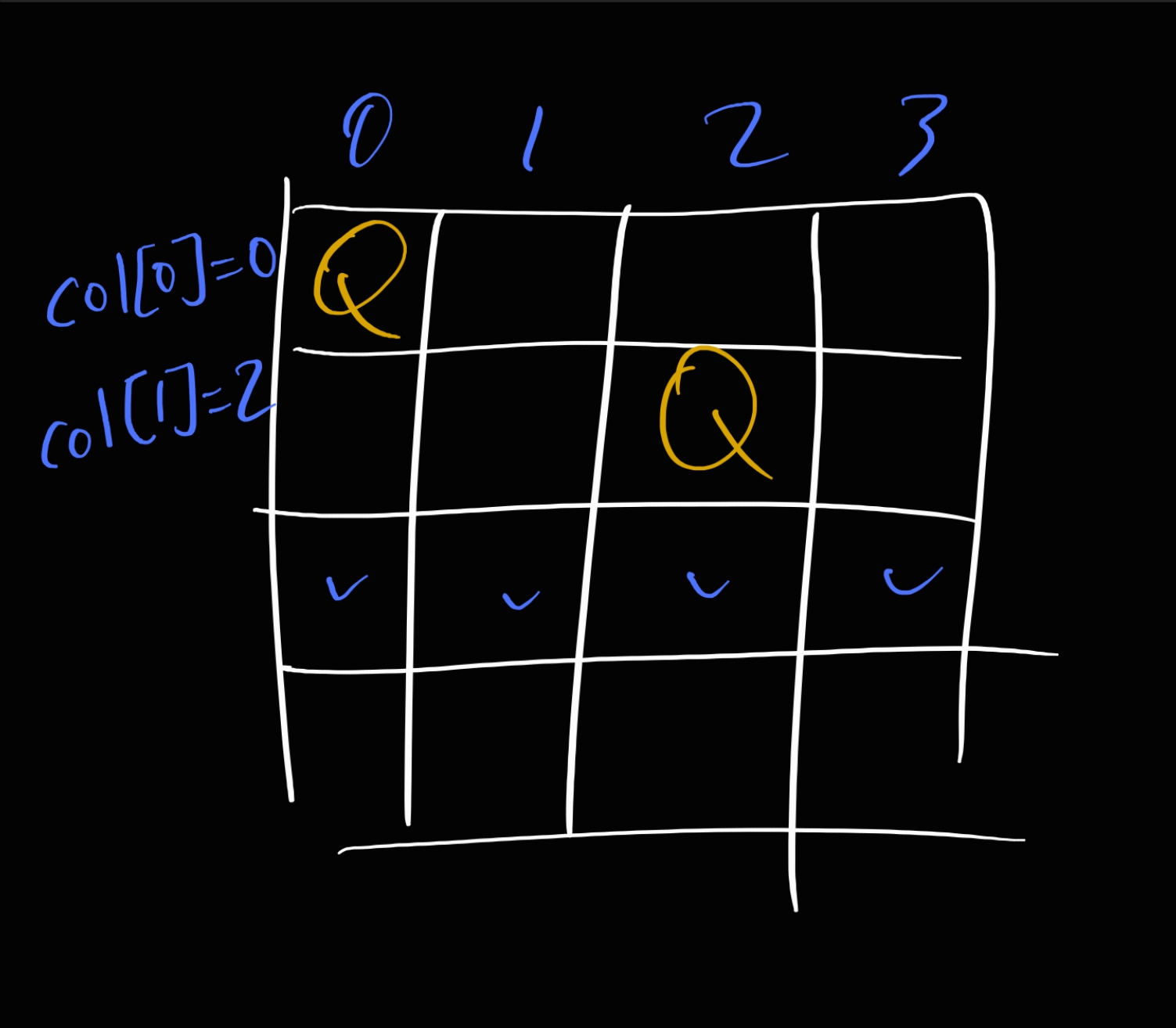
2번째 행에서 퀸이 배치 가능한 위치를 찾는다고 생각해보자.
먼저 현재 i=2이기 때문에 2번째 행에서 j=0부터 차례대로 퀸을 놓을 수 있는지 검사한다.
1차원 배열인 col은 현재 행에서 놓여진 퀸의 열 위치를 저장하기 때문에, j를 0부터 i-1까지 증가시키면서

1. 같은 열에 존재하는지

같은 열에 존재한다면 이전 행에 놓았던 퀸들의 열이 같을 것이다. col[i] == col[j]

2. 대각선 라인에 존재하는지

같은 대각선 라인에 존재하는 경우는 다음과 같다.
(0, 1)과 (1, 2)
그래서 |1-0| == |2-1|의 조건이 true가 된다면 (즉 행-행 == 열-열) 같은 대각선 라인에 있는 것이다.
(1, 3)과 (2, 2)의 경우에도 서로 같은 대각선 라인에 존재한다.
|1-2| == |3-2|

그래서 Placeable(2)를 호출하면 (2번째 행에서 현재 j열이 퀸이 놓여질 수 있는 위치인지 확인)
col[2] = 0, 즉 (2, 0) 위치에는 if(0 == 0)에서 true가 일어나기 때문에 false를 리턴
col[2] = 1, 즉 (2, 1) 위치에는 if(1 == 0)에서 false이고 if(abs(1-0) == (2-0))이 false이지만 if(0 == 1)에서 false, if(abs(1-2) == (2-1))에서 true가 일어나기 때문에 false를 리턴
col[2] = 2, 즉 (2, 2) 위치에서는 if(0 == 2)에서 false이지만 if(2 == 2)에서 true, if(abs(2-2) == 2-2)에서 true가 일어나서 false를 리턴
col[2] = 3, 즉 (2, 3) 위치에서도 마찬가지로 false를 리턴

---

제출코드

#include <iostream>

using namespace std;

int n; // 체스판 n x n
int cnt;
int* col;

bool Placeable(int i)
{
	for (int j = 0; j < i; j++)
		if (col[j] == col[i] || abs(col[i] - col[j]) == (i - j))
			return false;
	return true;
}

void DFS(int i) 
{
	if (i == n) 
		cnt++; 
	else
	{
		for (int j = 0; j < n; j++) 
		{
			col[i] = j;
			if (Placeable(i)) 
				DFS(i + 1);
		}
	}
}

int main(int argc, char* argv[])
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);

	cin >> n;
	col = new int[n];
	DFS(0);
	cout << cnt;

	return 0;
}