문제 링크

설명

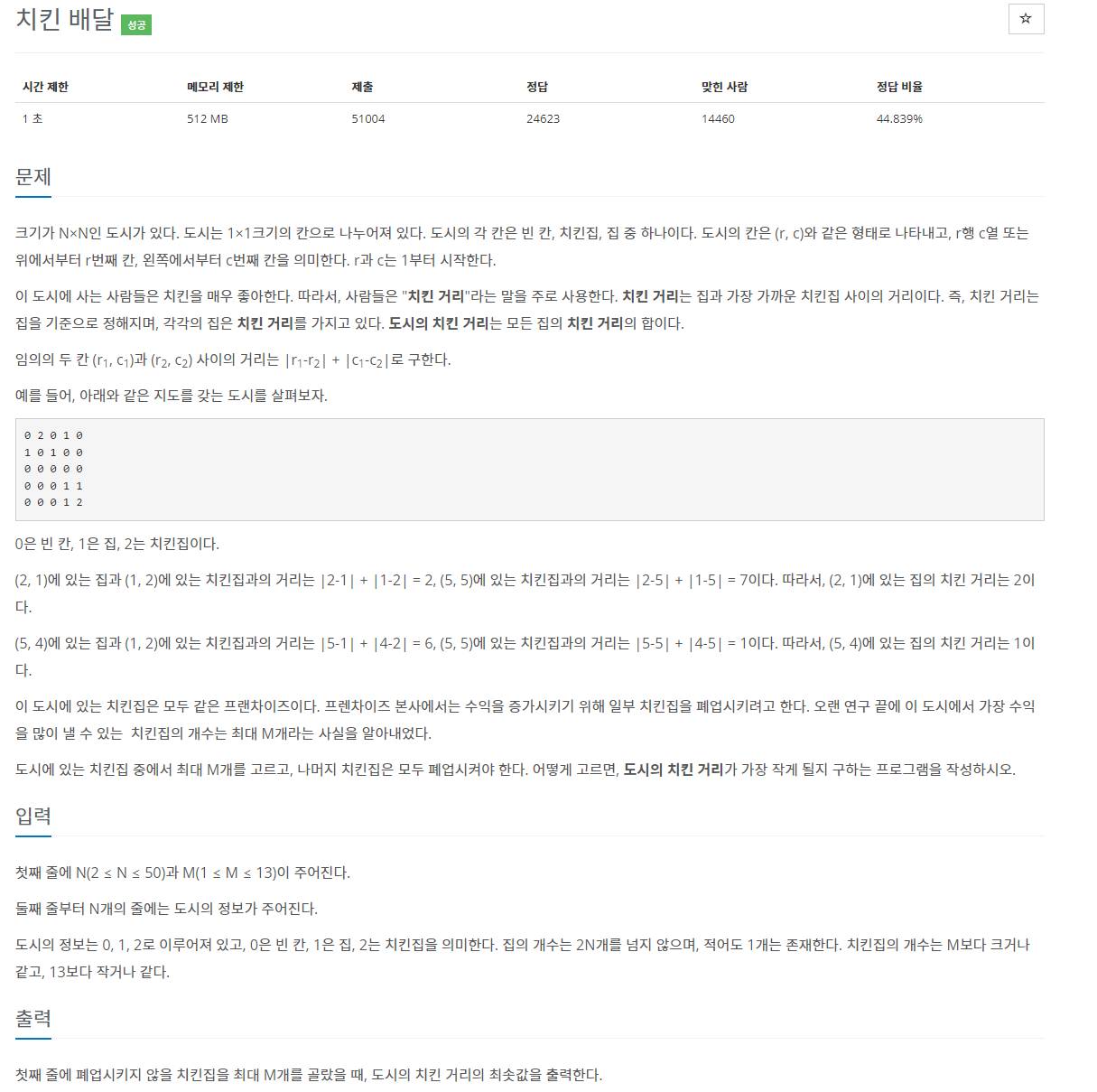
각각의 집과 모든 치킨집과의 거리를 구하여 각 집마다 최소 치킨거리를 구하고, 최대 m개의 치킨집을 살려뒀을 때 도시의 치킨거리 최소값을 구하는 문제이다.

치킨집 개수는 m보다 크거나 같고, 최대 m개의 치킨집을 살려둬야 한다.
만약 치킨집 개수가 10개이고 최대 5개의 치킨집을 살려둬야 했을 때 사실상 5개의 치킨집을 살려둬야 도시의 최소 치킨거리를 구할 수 있다. (최대 m개이지만 치킨집이 적을 수록 집과의 거리가 멀어지게 되니 사실상 m개의 조합을 구해야 한다.)

예제 입력 2에서 치킨집 5개 중에서 2개를 골라야하기 때문에 조합 알고리즘을 통해 치킨집을 골라야 한다.
A, B, C, D, E 중에서
(A, B)
(A, C)
(A, D)
...
고르면서 각 집들을 순회하며 A와 B 중 가까운 치킨집과의 거리를 골라 정답 변수에 더해주면 된다.

코드

#define _CRT_SECURE_NO_WARNINGS

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

vector<pair<int, int>> house, chicken, v;
bool selected[13];
int n, m, ans = 999999; // m : 최소 치킨집 개수

int CalDist() // 하나의 집과 살아남은 모든 치킨집의 거리
{
	int result = 0;

	for (int i = 0; i < house.size(); i++)
	{
		int shortest = 999999;
		for (int j = 0; j < v.size(); j++) // 가장 작은 거리 찾기
		{
			int dist = abs(v[j].first - house[i].first) + abs(v[j].second - house[i].second);
			shortest = min(shortest, dist);
		}
		result += shortest;
	}

	return result;
}

void DFS(int idx, int cnt)
{
	if (cnt == m) // "도시에 있는 치킨집 중에서 최대 m개를 고르고"
	{
		ans = min(ans, CalDist());
		return;
	}

	for (int i = idx; i < chicken.size(); i++)
	{
		if (selected[i]) continue;
		selected[i] = true;
		v.push_back(chicken[i]);

		DFS(i, cnt + 1);

		v.pop_back();
		selected[i] = false;
	}
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	cin >> n >> m;
	int input;

	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cin >> input;
			if (input == 1) house.push_back(make_pair(i, j));
			else if (input == 2) chicken.push_back(make_pair(i, j));
		}
	}

	DFS(0, 0);
	cout << ans;

	return 0;
}