99클럽 코테 스터디 22일차 TIL | Pascal's Triangle2

🖥️ 문제

Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.

In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:

📝 풀이

import java.util.*;

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> pascalTriangle = new ArrayList<>();

        // 각 행을 순차적으로 생성
        for (int i = 0; i < numRows; i++) {
            // 새로운 행 생성 (1로 시작)
            List<Integer> row = new ArrayList<>();
            for (int j = 0; j <= i; j++) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(pascalTriangle.get(i - 1).get(j - 1) + pascalTriangle.get(i - 1).get(j));
                }
            }
            pascalTriangle.add(row);
        }
        
        return pascalTriangle;
    }
}

첫번째는 깊은 생각을 하지 않고 지난 코드에서 얍쌉하게 바꾸는 방식으로 구현했다. 물론, 문제는 쉽게 풀렸지만 이렇게 문제를 풀 바엔 코더나 하는 게 나아서 정신 차리고 두번째 풀이를 시작했다.

import java.util.*;

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<>();
        row.add(1);
        
        for (int k = 1; k <= rowIndex; k++) {
            long nextElement = (long) row.get(k - 1) * (rowIndex - k + 1) / k;
            row.add((int) nextElement);
        }
        
        return row;
    }
}

사실 이문제는 파스칼을 검색하다가 이항계수를 알게 돼서 쓴 풀이방법이다. 삼각형에서 각 행의 숫자는 이항 계수로 표현할 수 있다. 즉, 행의 k번째 숫자는 아래의 공식에 따른다.

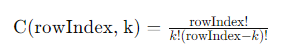
하지만 문제에서 오버플로우가 발생했고, long를 활용하여 다시 풀었다... (물론, 내 머리 30% 챗지비티70% 정도의...)

👀 고찰

막상 수학의 풀이방법을 이해해도 그걸 코딩으로 적으려니 넘 어려웠다. 뼛속부터 문과출신이라 그런가 이해부터 한참 걸렸고, 최적의 계산을 하려고 노력하니 눈물이 눈앞을 가렸다...😂