99클럽 코테 스터디 36일차 TIL | 적어도 대부분의 배수

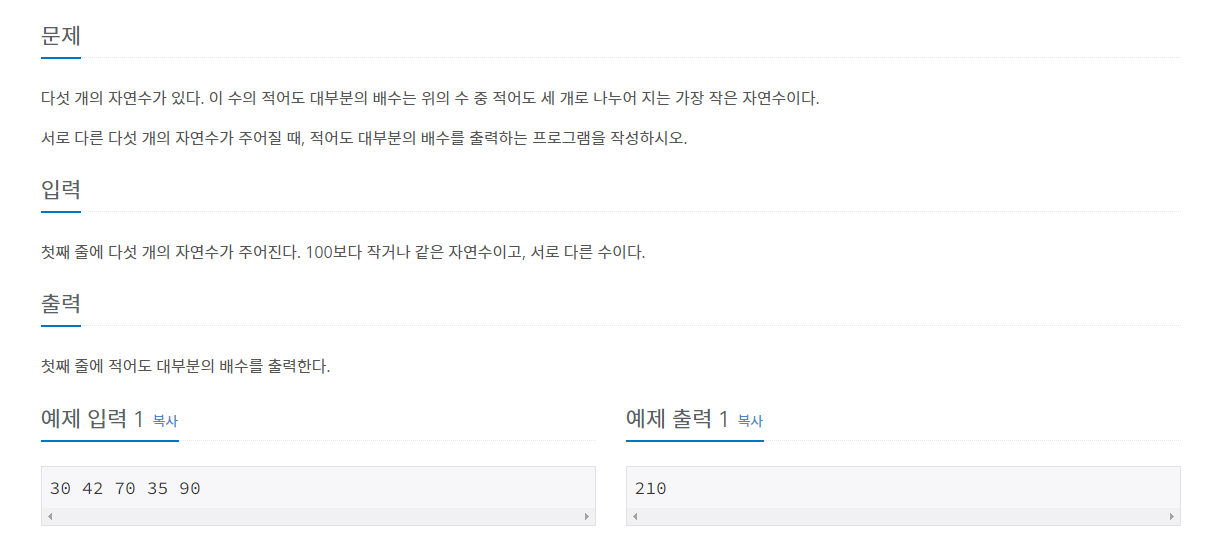
🖥️ 문제

📝 풀이

import java.util.Scanner;

public class Main {

    // 최대공약수(GCD) 계산 함수
    public int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }

    // 최소공배수(LCM) 계산 함수
    public int lcm(int a, int b) {
        return a * (b / gcd(a, b));
    }

    // 세 수의 최소공배수를 구하는 함수
    public int lcm(int a, int b, int c) {
        return lcm(lcm(a, b), c);
    }

    public void findMinimumLCM() {
        Scanner scanner = new Scanner(System.in);

        int[] numbers = new int[5];
        for (int i = 0; i < 5; i++) {
            numbers[i] = scanner.nextInt();
        }

        int minLCM = Integer.MAX_VALUE;

        // 5개 중 3개를 고르는 모든 조합에 대해 최소공배수를 계산
        for (int i = 0; i < 5; i++) {
            for (int j = i + 1; j < 5; j++) {
                for (int k = j + 1; k < 5; k++) {
                    int currentLCM = lcm(numbers[i], numbers[j], numbers[k]);
                    if (currentLCM < minLCM) {
                        minLCM = currentLCM;
                    }
                }
            }
        }

        System.out.println(minLCM);

        scanner.close();
    }

    public static void main(String[] args) {
        Main mainInstance = new Main();
        mainInstance.findMinimumLCM();
    }
}

문제에서 요구하는 적어도 대부분의 배수란 적어도 세 개의 수로 나누어지는 가장 작은 수를 의미하므로, 이 방법을 사용하여 계산했다.

GCD (Greatest Common Divisor) 두 수의 최대공약수는 두 수의 공통된 약수 중 가장 큰 값
LCM (Least Common Multiple) 두 수의 최소공배수는 두 수로 나누어지는 가장 작은 자연수