[BOJ] 1010 다리놓기 (Week 8, No.3)

문제

재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)

재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

입력

입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.

출력

각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.

예제 입력 1

3
2 2
1 5
13 29

예제 출력 1

1
5
67863915

---

풀이

m개의 다리 중 n개의 다리를 고르는 경우의 수를 구하는 문제이다.
교차되는 다리가 없어야 하므로 순서는 상관하지 않는다.
조합으로 구할 수 있다.
하지만 범위가 너무 커져버려서 숫자가 커지면 답을 구하지 못하는 경우가 나왔다. (예. n=28, m=29)

그래서 dp테이블을 이용했다.
예시) n=4, m=7

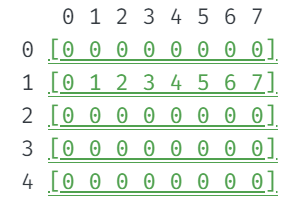
• n = 1일 때 dp[1][j] = j를 넣어주었다.
  

• n >= 2일 때
  현재 좌표의 왼쪽 값이 0인 경우, 왼쪽 대각선 위의 값이 현재 값이 된다.
  아닌 경우, 왼쪽 대각선 위의 값 + 왼쪽 값이 현재 값이 된다.
  

• 최종 dp 테이블
  

마지막으로 dp[n][m]을 반환한다.

---

코드

조합(실패)

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int T = sc.nextInt();

        if (T == 0) {
            return;
        }

        for (int i = 0; i < T; i++) {
            int N = sc.nextInt();
            int M = sc.nextInt();

            if (N == 1) {
                System.out.println(M);
                return;
            }

            long m = 1;
            for (int j = M; j > M - N; j--) {
                m *= j;
            }
            for (int j = N; j >= 1; j--) {
                m /= j;
            }
            
            System.out.println(m);
        }
    }
}

DP(성공)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());
        for (int t = 0; t < T; t++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            int M = Integer.parseInt(st.nextToken());

            // base case
            if (N == 1) {
                System.out.println(M);
                continue;
            }
            if (N == M) {
                System.out.println(1);
                continue;
            }

            long[][] dp = new long[31][31];

            for (int i = 1; i <= M; i++) {
                dp[1][i] = i;
            }

            for (int i = 2; i <= N; i++) {
                for (int j = i; j <= M; j++) {
                    dp[i][j] = dp[i - 1][j - 1];
                    if (j != i) {
                        dp[i][j] += dp[i][j - 1];
                    }
                }
            }
            System.out.println(dp[N][M]);
        }
    }
}