[LeetCode] 289 Game of Life

Description

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.

Example 1:

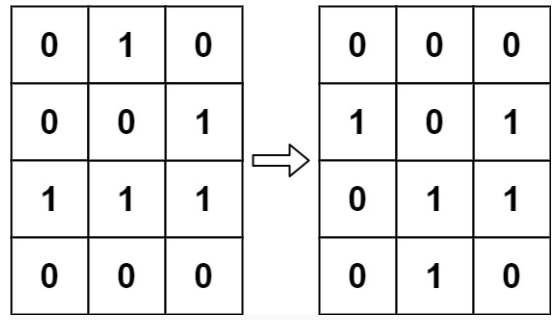
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

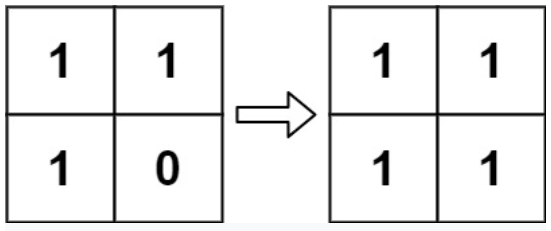
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] is 0 or 1.
  
  

---

풀이

• 이차원 배열은 0 또는 1로만 구성되어 있다.

• 삶과 죽음은 함께 일어난다.

• 나를 둘러싼 8명의 이웃 중 살아있는 이웃 수에 따라 내가 죽거나 살 수 있다.

<규칙>
1. 내가 살았을 때 2명 미만의 이웃이 살았다 -> 나는 죽는다.
2. 내가 살았을 때 2, 3명의 이웃이 살았다 -> 그대로 산다.
3. 내가 살았을 때 세 명 이상의 이웃이 살았다 -> 나는 죽는다.
4. 내가 죽었을 때 세 명의 이웃이 살았다 -> 나는 살아난다.

• 우선 삶과 죽음이 함께 일어나므로 기존에 저장된 값을 보며 조건을 적용시켜야 한다. 그래서 새로운 이차원 배열에 기존 값을 복사해둔다.

• 나를 둘러싼 8명의 이웃 좌표로 쉽게 가기 위해 xy 이차원 배열에 움직여야 할 각 좌표의 차이를 저장해둔다.

• 복사해둔 배열의 행렬을 모두 돈다.

• xy 배열에 저장해 둔 좌표들을 하나씩 적용하면서 이웃의 좌표를 구한다.

• 이웃의 좌표가 범위 안에 있고, 값이 1일 때, 즉 살아있을 때 개수를 센다.

• 그 후 위의 4개의 규칙을 적용한다.

  <코드 순서대로>
  1번 규칙 -> 기존 배열에서 현 좌표값은 0으로 바꾼다. (죽음)
  2번 규칙 -> 기존 배열의 현 좌표값은 그대로 유지된다.
  4번 규칙 -> 기존 배열에서 현 좌표값을 1로 바꾼다. (삶)
  3번 규칙 -> 기존 배열에서 현 좌표값은 0으로 바꾼다. (죽음)

• 이렇게 기존에 주어진 배열이 새로운 값들로 변경된다.
  
  

• 각 행렬을 한번만 돌고, 값을 저장하는 이차원 배열이 2개만 있으므로 시간과 공간복잡도 모두 O(N)이 된다.
  
  

---

코드

class Solution {
    public void gameOfLife(int[][] board) {
        int[][] copyBoard = new int[board.length][board[0].length];
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                copyBoard[i][j] = board[i][j];
            }
        }
        int[][] xy = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};
        int count, neighborX, neighborY;
        for (int i = 0; i < copyBoard.length; i++) {
            for (int j = 0; j < copyBoard[0].length; j++) {
                count = 0;
                for (int k = 0; k < xy.length; k++) {
                    neighborX = i + xy[k][0];
                    neighborY = j + xy[k][1];
                    if (neighborX >= 0 && neighborX < copyBoard.length && neighborY >= 0 && neighborY < copyBoard[0].length && copyBoard[neighborX][neighborY] == 1) {
                        count++;
                    }
                }
                if (copyBoard[i][j] == 1 && count < 2) board[i][j] = 0;
                else if (copyBoard[i][j] == 1 && count <= 3) board[i][j] = copyBoard[i][j];
                else if (copyBoard[i][j] == 0 && count == 3) board[i][j] = 1;
                else if (copyBoard[i][j] == 1 && count > 3) board[i][j] = 0;
            }
        }
    }
}