해시

: 임의의 크기를 가진 데이터를 고정된 데이터의 크기로 변환시키는 것.
특정한 배열의 인덱스나 위치를 입력하고자 하는 데이터값을 이용해 저장하거나 찾을 수 있다.
해시를 이용하면 즉시 저장하거나 찾고자 하는 위치를 참조할 수 있으므로 더욱 빠른 속도로 처리할 수 있다.

Direct Addressing Table

: 키-값 쌍의 데이터를 배열에 저장할 때, 키값을 직접적으로 배열의 인덱스로 사용하는 방법.
똑같은 키가 없다고 가정할 때 찾고자 하는 데이터의 키만 알고 있으면 즉시 위치를 찾을 수 있으므로 crud 모두 선형시간 (O(1)) 으로 처리할 수 있다.
다만, 키 값의 최대 크기만큼 배열이 할당되어 주의가 필요하다.

Hash Table

: 키-값 쌍에서 키 값을 테이블에 저장할 때, 키값을 함수로 이용해 계산을 수행한 후, 그 결과값을 배열의 인덱스로 사용하여 저장하는 방식.
여기서 키값을 계산하는 함수는 해쉬함수다.
해쉬함수는 입력으로 키를 받아 0부터 배열의 크기-1 사이의 값을 출력한다.
해쉬에 대한 첫 정의대로 임의의 숫자를 배열의 크기만큼으로 변환시킨 것.
이 경우 k값이 h(k)로 해쉬되었다고 하며, h(k)는 k의 해쉬값이라고 한다.

Open Addresing

: 모든 데이터(키-값)를 테이블에 저장하는 방법.
장점 - 데이터를 모두 직접 읽어와서 포인터를 사용하지 않는다. 그로인해 발생할 수 있는 오버헤드를 방지할 수 있다.
포인터가 필요없어 구현이 용이해지고, 포인터 접근에 필요한 시간이 없어 큰 성능이 향상된다.

스택/큐

스택(Stack)

: 데이터를 쌓아놓은 자료구조. 선입후출(LIFO). 먼저 들어오고 나중에 들어온게 나간다.

ex. 뒤로가기

• 삽입(push) : 마지막 데이터 위치에 요소를 넣는다.
• 삭제(pop) : 제일 마지막에 넣은 요소를 지운다.
• 읽기(peek) : 제일 마지막에 넣은 요소를 읽는다.

큐(Queue)

: 데이터를 쌓아놓은 자료구조. 선입선출(FIFO). 먼저 들어오고 먼저 들어온게 나간다.

ex. 줄서기

• 삽입(enqueue):큐 맨 뒤에 데이터를 넣는다.
• 삭제(dequeue):큐 맨 앞의 요소를 지운다.
• 읽기(peek): front에 위치한 데이터를 읽는다.
• 큐의 맨 앞(front): 큐 맨 앞의 위치
• 큐의 맨 뒤(rear): 큐 맨 뒤의 위치

힙(Heap)

: 완전 이진 트리의 일종. 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조.
일종의 반정렬 상태(느슨한 정렬 상태)를 유지한다.

• 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도.
  -> 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리
  중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)

힙으로 우선순위 큐를 구현할 수 있다.

종류

• 최대 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리 (위->아래 - 큰 -> 작은)
• 최소 힙 : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리 (위->아래 - 작은 -> 큰)

힙을 저장하는 표준적인 자료구조 -> 배열

정렬

: 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘.
효율적인 정렬은 탐색이나 병합 알고리즘처럼 다른 알고리즘을 최적화하는데 중요하다.
데이터의 정규화나 이미있는 결과물을 생성하는 데 흔히 유용하게 쓰인다.
만족해야 할 두 조건
1. 출력은 비 내림차순이다. (각각의 원소가 전 순서 원소에 비해 이전의 원소보다 작지 않은 순서)
2. 출력은 입력을 재배열하여 만든 순열이다.

단순 정렬

: 작은 데이터에 효율적. 큰 데이터에는 비효율적.

삽입 정렬, 선택 정렬

효율적인 정렬

: 다양한 수정이 수반되는 실생활 데이터를 기준으로 랜덤 데이터에 점근적으로 효율적이다.
평균 시간 복잡도 - O(NlogN)

합병 정렬, 힙 정렬, 퀵 정렬, 셸 정렬

거품 정렬 및 변종

거품 정렬, 빗질 정렬

분산 정렬

계수 정렬, 버킷 정렬, 기수 정렬

완전탐색

: 가능한 모든 경우의 수를 다 체크해서 정답을 찾는 방법.
-> 무식하게 가능한거 다 해볼거야!
a.k.a. Brute Force
직관적이어서 이해하기 쉽고, 문제의 정확한 결과값을 얻어낼 수 있는 가장 호가실하며 기초적인 방법.

고려할 점

1. 해결하고자 하는 문제의 가능한 경우의 수를 대력적으로 계산한다.
2. 가능한 모든 방법을 다 고려한다.
3. 실제 답을 구할 수 있는지 적용한다.

2번의 방법들

1. Brute Force 기법 - 반복/조건문을 활용하여 모두 테스트하는 방법
2. 순열(permutation) - n개의 원소 중 r개의 원소를 중복 허용 없이 나열하는 방법
3. 재귀 호출
4. 비트마스크 - 2진수 표현 기법 활용
5. BFS, DFS 활용

출처

탐욕법(Greedy)

부분적인 최적해가 전체적인 최적해가 된다.

: 미래를 생각하지 않고 각 단계에서 가장 최선의 선택을 하는 기법. 각 단계에서 최선의 선택을 한 것이 전체적으로 최선이길 바란다. 모든 경우는 아니지만 이 방법이 통하는 경우가 있다.

DP 사용 시 지나치게 많은 일을 한다는 것에 착안하여 고안된 알고리즘. DP와 같이 쓰이며 서로 보완하는 개념이다.

a.k.a 탐욕 알고리즘, 그리디 알고리즘, 욕심쟁이 알고리즘

활동 선택 문제

-> 한 강의실에서 여러 개의 수업을 하려고 할 때, 한 번에 가장 많은 수업을 할 수 있는 경우 고르기

분할 가능 문제

-> 무게가 초과하기 전까지 물건을 쪼개가며 가장 많은 짐을 넣는 방법

동적계획법(Dynamic Programming)

불필요한 계산을 줄이고, 효율적으로 최적해를 찾아야만 풀리는 문제

: 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법. 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다.

각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 저장된 값을 불러와 사용한다. -> 계산 횟수가 줄어든다.

하위 문제의 수가 기하급수적으로 증가할 때 유용하다.

최단 경로 문제, 행렬의 제곱 문제 등의 최적화에 사용된다.

DP를 적용하기 위한 조건

1. 큰 문제를 작은 문제들로 나눌 수 있는가?
2. 작은 문제들의 답으로 큰 문제의 답을 구할 수 있는가?
3. 작은 문제들의 답이 반복적으로(중복되어) 나오는가?

동적 계획법은 그리디 알고리즘에 비해 시간적으로는 효율적이지 못할 수는 있어도, 그 결과에 대해서는 효율적인 값을 구할 수가 있다.

깊이/너비 우선 탐색(DFS/BFS)

깊이 우선 탐색(DFS)

: 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

한 방향으로 갈 수 있을 때까지 계속 가다가 더이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와 이곳부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.

깊게 탐색.
모든 노드를 방문해야 할 때 사용한다.
bfs보다 간단한다.
단순 검색 속도는 bfs보다 느리다.

특징

• 자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있다.
• 전위 순회를 포함한 다른 형태의 트리 순회는 모두 dfs의 한 종류이다.
• 어떤 노드를 방문했는지 여부를 반드시 검사해야 한다. (안하면 무한루프)

방법

현재 노드와 인접한 노드를 꼬리에 꼬리를 물어 순회한다.
더 갈 수 없을 경우, 이전 노드로 돌아와 위와 같이 순회한다.

구현

순환 호출 이용
명시적인 스택 사용 (방문한 정점들을 스택에 저장하였다 꺼내서 작업한다.)

출처

너비 우선 탐색(BFS)

: 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법

시작 정점으로부터 가까운 정점을 먼저 모두 방문하고, 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

넓게 탐색
두 노드 사이의 최단 경로, 임의의 경로를 찾고 싶을 때 사용한다.
dfs보다 좀 더 복잡하다.

특징

직관적이지 않은 면이 있다.
재귀적으로 동작하지 않는다.
어떤 노드를 방문했는지 여부를 반드시 검사해야 한다. (안하면 무한루프)

구현

선입선출을 원칙으로 탐색하는 큐를 사용한다.
prim, dijkstra 알고리즘과 유사하다.

출처

이분탐색

: 탐색 기법중에 하나. 원하는 탐색 부위를 두 부분으로 분할하여 찾는 방식. 원래의 전부를 탐색하는 탐색 속도에 비해 빠르다.

방법

1. 정렬하기
2. left, right로 mid값을 잡아준다. (mid = (left + right)/2)
3. mid 값과 구하고자 하는 값을 비교한다.
4. 비교할 시 mid 값보다 구하고자 하는 값이 높으면 left를 mid+1로 만들어주고, 낮으면 right를 mid-1로 만들어준다.
5. left > right가 될 때까지 1~3을 반복하여 구하고자 하는 값을 찾는다.

시간복잡도

전체 검색: O(N)
이분 탐색: O(logN)

출처

그래프

: 정점(vertex)과 간선(edge)으로 이루어진 자료구조. 정점간의 관계를 표현하는 조직도.

-> 트리도 그래프의 일종이다.

그래프가 트리와 다른 점

정점마다 간선이 없을 수도 있고 있을 수도 있다.
루트노드, 부모와 자식의 개념이 없다.

이 그래프를 순회하는 방식을 잘 알아야 한다.

• DFS, BFS

그래프에서 사용하는 용어

• 정점(vertex): a.k.a 노드(node) 정점에는 데이터가 저장된다.
• 간선(edge): a.k.a 링크 노드간의 관계를 나타낸다.
• 인접 정점(adjacent vertex): 간선에 의해 연결된 정점.
• 단순 경로(simple-path): 경로 중 반복되는 정점이 없는 것. 같은 간선을 지나가지 않는 경로.
• 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수.
• 진출 차수(out-degree): 방향 그래프에서 사용되는 용어. 한 노드에서 외부로 향하는 간선의 수.
• 진입 차수(in-degree): 방향 그래프에서 사용되는 용어. 외부 노드에서 들어오는 간선의 수.

그래프 구현 방법

인접 행렬(Adjacency Matrix), 인접 리스트(Adjacency List)

인접 행렬

: 그래프의 노드를 2차원 배열로 만든 것.

• 장점

1. 2차원 배열안에 모든 정점들의 간선 정보를 담는다. 그래서 배열의 위치를 확인하면 두 점에 대한 연결 정보를 조회할 때 O(1)의 시간복잡도로 가능하다.
2. 구현이 비교적 간단하다.

• 단점

1. 모든 정점에 대해 간선 정보를 대입해야 하므로 O(n^2)의 시간복잡도가 소요된다.
2. 무조건 2차원 배열이 필요하므로 필요 이상의 공간이 낭비된다.

인접 리스트

: 그래프의 노드들을 리스트로 표현한 것. 주로 정점의 리스트 배열을 만들어 관계를 설정해줌으로써 구현한다.

• 장점

1. 정점들의 연결 정보를 탐색할 때 O(N)의 시간이면 가능하다.
2. 필요한 만큼의 공간만 사용하므로 공간의 낭비가 적다.

• 단점

1. 특정 두 점이 연결되었는지 확인하려면 인접 행렬에 비해 시간이 오래걸린다.
2. 구현이 비교적 어렵다.

다양한 그래프의 종류

• 무방향 그래프
  : 두 정점을 연결하는 간선에 방향이 없는 그래프

• 방향 그래프
  : 두 정점을 연결하는 간선에 방향이 존재하는 그래프. 간선의 방향으로만 이동할 수 있다.

• 가중치 그래프
  : 두 정점을 이동할 때 비용이 드는 그래프

• 완전 그래프
  : 모든 정점이 간선으로 연결되어 있는 그래프

그래프 탐색

• 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
  ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자회로에서 특정 단자와 단자가 서로 연결되어 있는지

출처

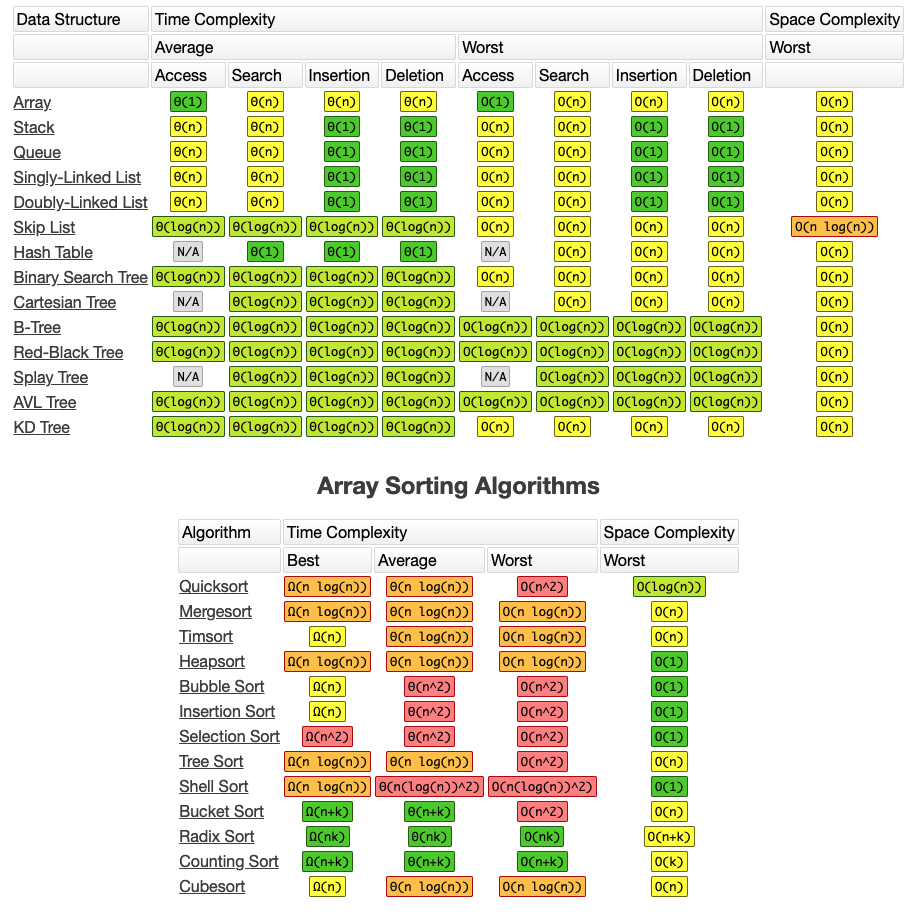
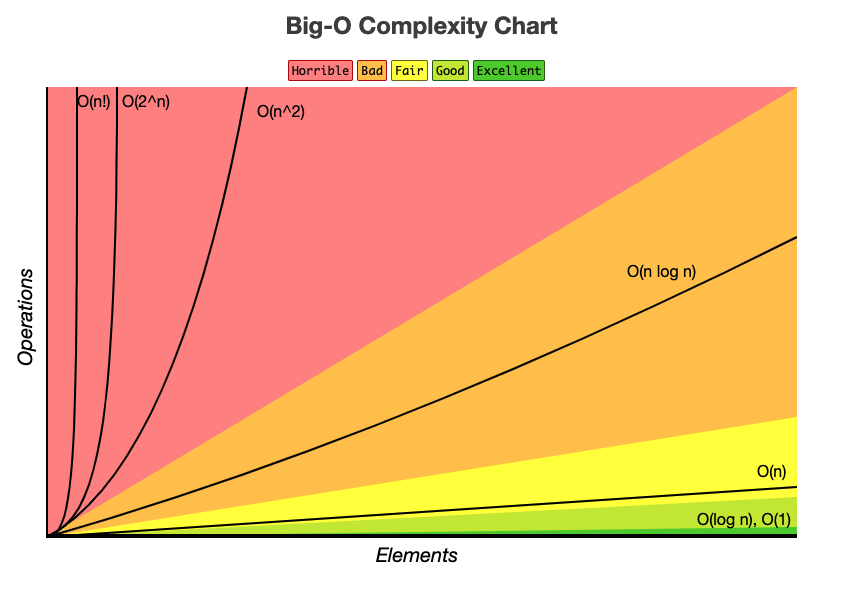
시간복잡도 표