1. Implicit List

가장 간단한 유형이다. 여러가지 종류를 구현하기에 용이하다. find_fit함수만 수정해가며 구현했다.

1) 종류

A. first-fit

static void *find_fit(size_t asize)
{
    void *bp = mem_heap_lo() + 2 * WSIZE; // 첫번째 블록(주소: 힙의 첫 부분 + 8bytes)부터 탐색 시작
    while (GET_SIZE(HDRP(bp)) > 0)
    {
        if (!GET_ALLOC(HDRP(bp)) && (asize <= GET_SIZE(HDRP(bp)))) // 가용 상태이고, 사이즈가 적합하면
            return bp;                                             // 해당 블록 포인터 리턴
        bp = NEXT_BLKP(bp);                                        // 조건에 맞지 않으면 다음 블록으로 이동해서 탐색을 이어감
    }
    return NULL;
}

처음부터 검색. 찾자마자 바로 리턴.

B. next-fit

static void *find_fit(size_t asize)
{
    void *bp;
    void *old_pointp = pointp;
    for (bp = pointp; GET_SIZE(HDRP(bp)); bp = NEXT_BLKP(bp))
    {
        if (!GET_ALLOC(HDRP(bp)) && GET_SIZE(HDRP(bp)) >= asize)
        {
            pointp = NEXT_BLKP(bp);
            return bp;
        }
    }
    for (bp = heap_listp; bp < old_pointp; bp = NEXT_BLKP(bp))
    {
        if ((!GET_ALLOC(HDRP(bp))) && GET_SIZE(HDRP(bp)) >= asize)
        {
            pointp = NEXT_BLKP(bp);
            return bp;
        }
    }
    return NULL;
}

마지막으로 탐색을 끝낸 위치(old_pointp)에서 탐색.
만약 못찾으면 2번째 for문이 실행. 처음부터 old_pointp까지 탐색함.

C. best-fit

static void *best_fit(size_t asize)
{
    void *bp = mem_heap_lo() + 2 * WSIZE;
    int flag = 1;
    char *best_fit_addr = bp;

    while (GET_SIZE(HDRP(bp)) > 0)
    {
        if (!GET_ALLOC(HDRP(bp)) && (asize <= GET_SIZE(HDRP(bp)))){ // 가용 상태이고, 사이즈가 적합하면
            if(flag) {
                best_fit_addr = bp;
                flag = 0;
                bp = NEXT_BLKP(bp);
                continue; 
            }
            if(*best_fit_addr > GET_SIZE(HDRP(bp))){
                best_fit_addr = bp;
            }
        }        // 해당 블록 포인터 리턴
        
        bp = NEXT_BLKP(bp); // 조건에 맞지 않으면 다음 블록으로 이동해서 탐색을 이어감
        
    }
    if (flag) return NULL;
    return best_fit_addr;
}

가장 적합한 크기의 블록을 찾아서 리턴.

2. Explicit List

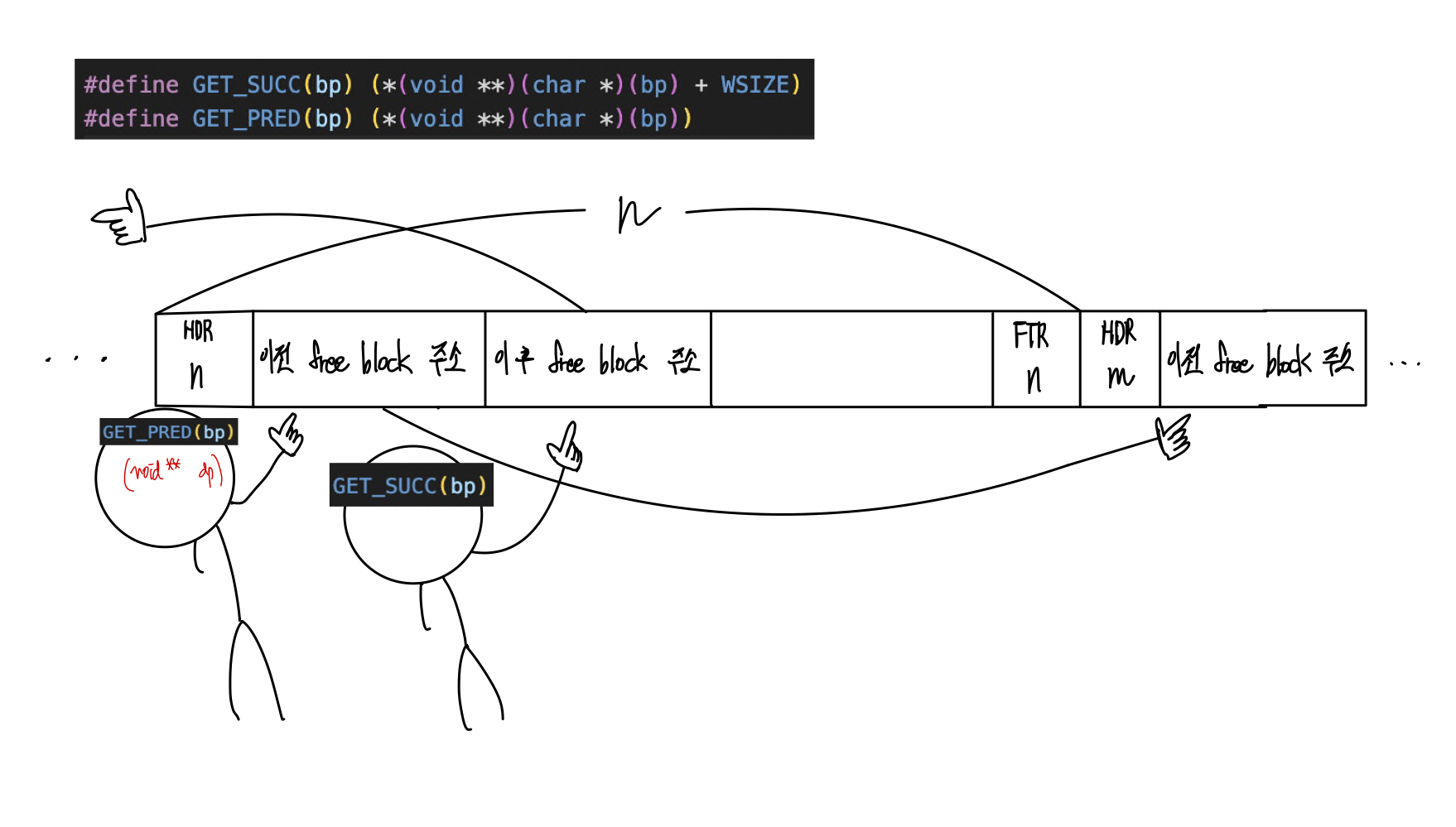
1) successor와 predecessor에 대한 이해

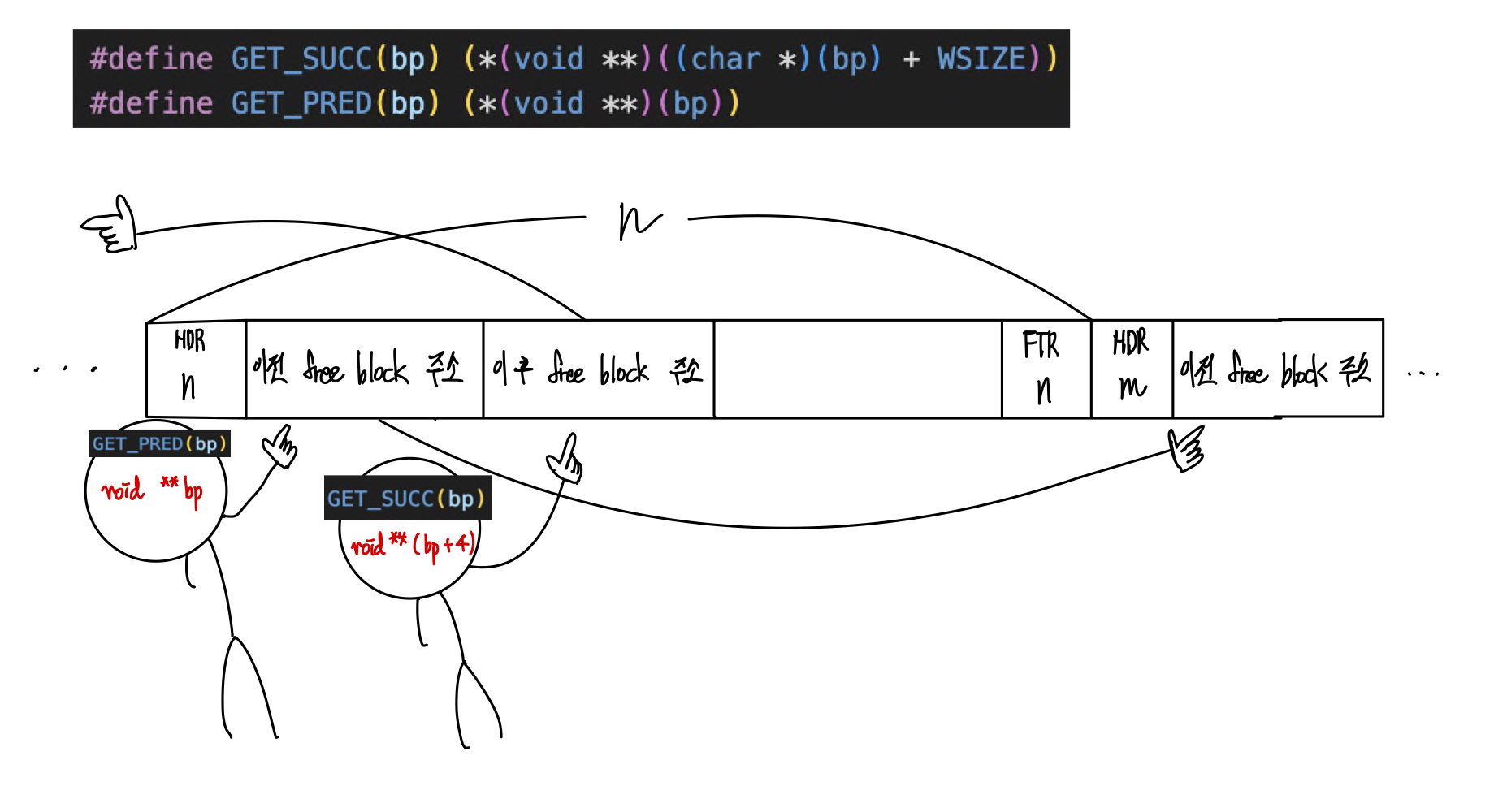
아래의 코드에서 HDR나 FTR에 저장된 값을 더하거나 빼면서 이전 블록과 다음 블록의 포인터를 찾고 있다. 위 그림을 보면서 아래 코드를 이해해보기 바란다.

2) place 함수에서 최소 블록 크기 16이상이어야만 분할한다.

3) explicit list도 coalesce는 연속된 메모리 주소를 검사한다.

나는 단순히 explicit은 coalesce에서 pred, 현재 bp, 그리고 succ을 coalesce할 것이라고 생각했다. 하지만 그게 아니었다.

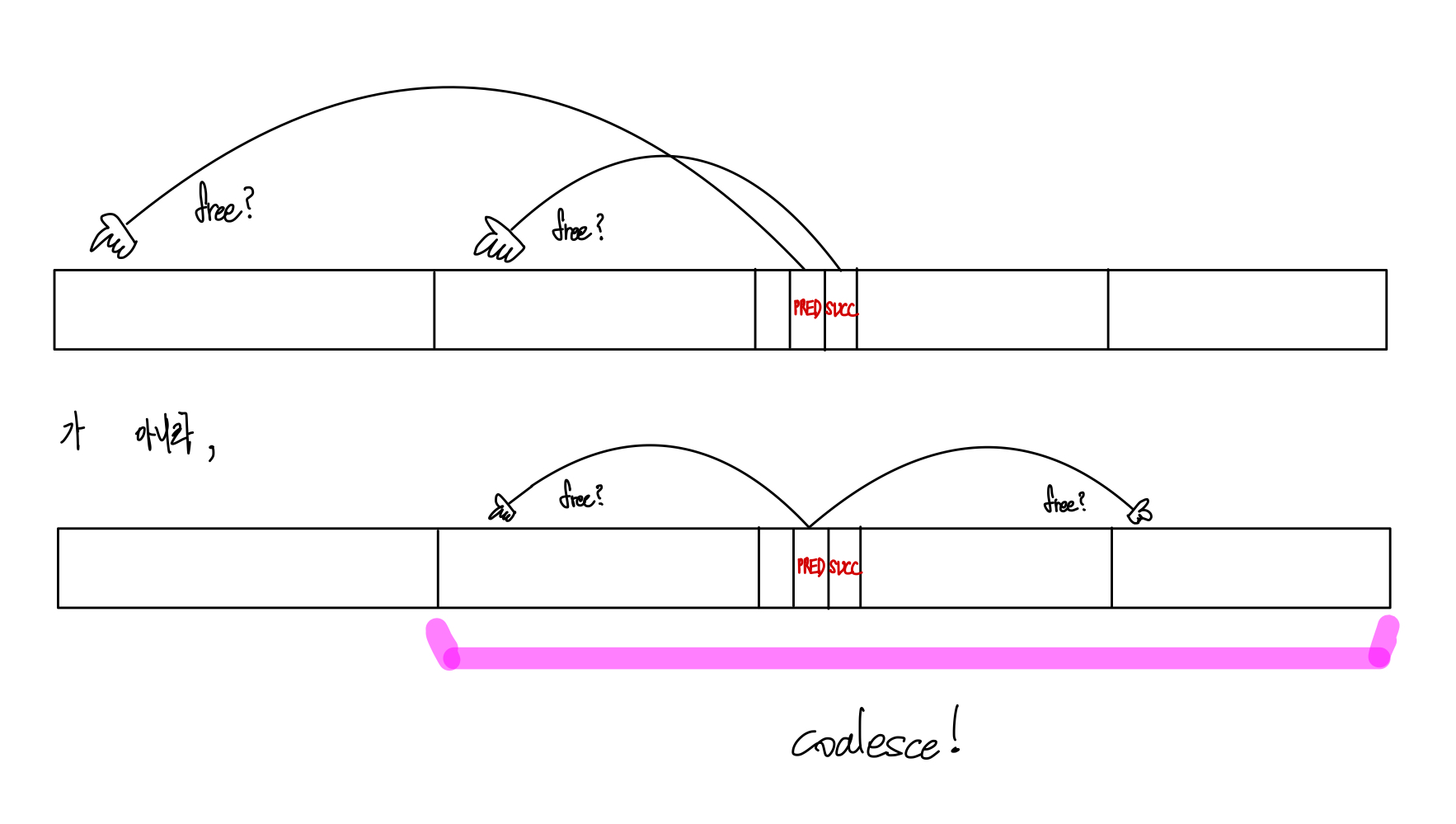
물리적 메모리 위치 상에서 연속된 위치를 coalesece하는 것으로 결국 implicit list와 동일했다.

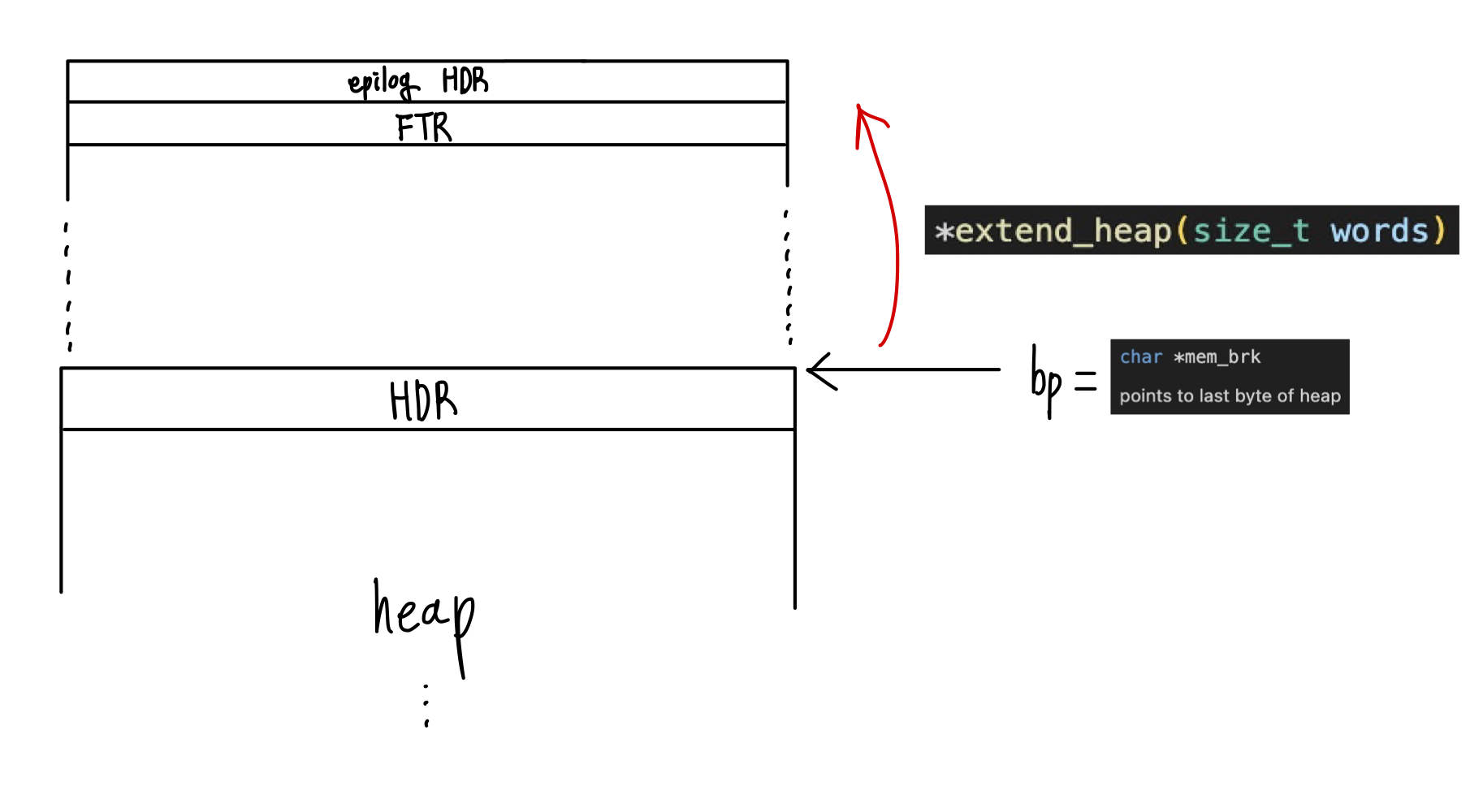
4) extend_heap 함수 내에서..

static void *extend_heap(size_t words)
{
    char *bp;

    // 더블 워드 정렬 유지
    // size: 확장할 크기
    size_t size = (words % 2) ? (words + 1) * WSIZE : words * WSIZE; // 2워드의 가장 가까운 배수로 반올림 (홀수면 1 더해서 곱함)

    if ((long)(bp = mem_sbrk(size)) == -1) // 힙 확장
        return NULL;

    PUT(HDRP(bp), PACK(size, 0));         // 새 빈 블록 헤더 초기화
    PUT(FTRP(bp), PACK(size, 0));         // 새 빈 블록 푸터 초기화
    PUT(HDRP(NEXT_BLKP(bp)), PACK(0, 1)); // 에필로그 블록 헤더 초기화

    return coalesce(bp); // 병합 후 coalesce 함수에서 리턴된 블록 포인터 반환
}

bp = mem_sbrk(size) 의 결과로 bp는 확장되기 전 힙의 마지막 주소를 가리킨다.

3. Segregated List

1) init 함수

int mm_init(void)
{
    if ((heap_listp = mem_sbrk((SEGREGATED_SIZE + 4) * WSIZE)) == (void *)-1) 
        return -1;
    PUT(heap_listp, 0);                                                    
    PUT(heap_listp + (1 * WSIZE), PACK((SEGREGATED_SIZE + 2) * WSIZE, 1)); // 프롤로그 Header (크기: 헤더 1 + 푸터 1 + segregated list 크기)
    for (int i = 0; i < SEGREGATED_SIZE; i++)
        PUT(heap_listp + ((2 + i) * WSIZE), NULL);
    PUT(heap_listp + ((SEGREGATED_SIZE + 2) * WSIZE), PACK((SEGREGATED_SIZE + 2) * WSIZE, 1)); // 프롤로그 Footer
    PUT(heap_listp + ((SEGREGATED_SIZE + 3) * WSIZE), PACK(0, 1));                             // 에필로그 Header: 프로그램이 할당한 마지막 블록의 뒤에 위치
    heap_listp += (2 * WSIZE);
    if (extend_heap(4) == NULL)
        return -1;
    if (extend_heap(CHUNKSIZE / WSIZE) == NULL)
        return -1;
    return 0;
}

위 코드를 간단히 표현하면 다음과 같다.

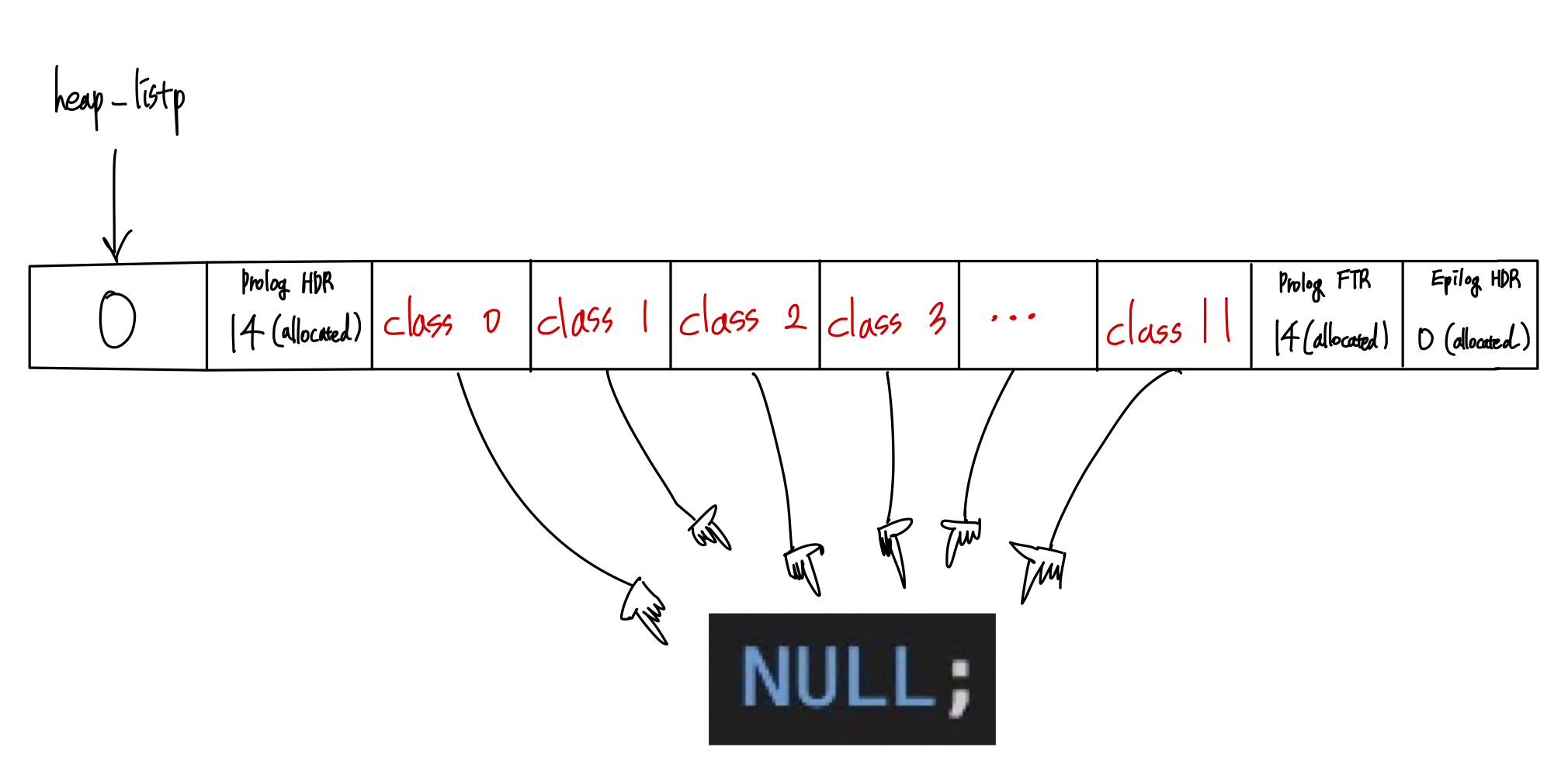
2) 종류

A. Simple-Segregated Storage - 단순 분리 저장

각 class는 8, 16, 32, ... 와 같이 2의 거듭제곱의 크기에 해당하는 free list를 저장한다.

malloc 호출 시, payload 사이즈에 next pointer 저장하기 위한 WSIZE(=4)를 더한 뒤 2의 거듭제곱으로 올림한 크기 n을 할당한다.

만약, 사이즈 n에 해당하는 class에 free list가 존재하지 않는 경우, extend_heap함수를 호출한다.

이 때 여기서 일반 segregated list와의 차이가 발생한다.

여기서는 extend된 힙의 사이즈를 모두 malloc을 요청한 사이즈 n에 해당하는 class의 크기로 잘라서 넣는다.
또한, coalesce과정을 거치지 않는다. 즉, 각각의 사이즈를 보존한 채로 free_list를 유지시킨다.

아래는 extend_heap함수 내에서 호출하는 divide_chunk함수이다.

static void divide_chunk(size_t adjust_size, void* bp){
    int index = find_index(adjust_size);
    segregated_free_list[index] = bp;
    while(1){
        if ((char*)bp + adjust_size > mem_heap_hi() - 3){
            PUT(NEXT(bp), 0);
            break;
        }
        PUT(NEXT(bp), (unsigned int*)((char*)bp + adjust_size));
        bp = GET(NEXT(bp));
    }
}

이름대로 단순(?)하게 한다는 의미를 제대로 이해할 수 있는 대목이다.

coalesce를 따로 하지 않고, extend된 힙을 하나의 class로 전부 할당한다는 극단적인 단순함 때문에 점수가 많이 나쁠 것 같았지만 예상보다 그리 나쁘지는 않았다. 이에 대한 고찰은 다음과 같다.

고찰 1. 제공된 테스트 데이터가 대체적으로 비슷한 크기로 이루어져 있기 때문

테스트 케이스를 확인하기 위해, mdriver.c를 뒤져보았다.

/* read every request line in the trace file */
    index = 0;
    op_index = 0;
    while (fscanf(tracefile, "%s", type) != EOF) {
	switch(type[0]) {
	case 'a':
	    fscanf(tracefile, "%u %u", &index, &size);
	    trace->ops[op_index].type = ALLOC;
	    trace->ops[op_index].index = index;
	    trace->ops[op_index].size = size;
	    max_index = (index > max_index) ? index : max_index;
	    break;
	case 'r':
	    fscanf(tracefile, "%u %u", &index, &size);
	    trace->ops[op_index].type = REALLOC;
	    trace->ops[op_index].index = index;
	    trace->ops[op_index].size = size;
	    max_index = (index > max_index) ? index : max_index;
	    break;
	case 'f':
	    fscanf(tracefile, "%ud", &index);
	    trace->ops[op_index].type = FREE;
	    trace->ops[op_index].index = index;
	    break;

다음은 테스트 케이스 파일 중 일부이다.

a 63 456
a 64 456
a 65 456
a 66 456
a 67 456
a 68 456
a 69 456
a 70 456
a 71 456
a 72 456
a 73 456
a 74 9
a 75 10
a 76 9
a 77 9
a 78 4072
a 79 9
a 80 9
a 81 9
a 82 9
a 83 9
a 84 10
a 85 9
a 86 9
a 87 9
a 88 9

즉, 테스트 케이스는 "Type(알파벳), Index(TC넘버링), Size(malloc size)" 로 이루어져 있다.
확인해보면, malloc size가 대체적으로 비슷한 TC들끼리 모여있음을 알 수 있다.
이는 구현한 simple_segregated_storage에서 선호하는 테스트 형식이다. 왜냐하면 extend된 힙을 사이즈에 맞는 class의 크기로 많이 잘라놓으므로 비슷한 크기의 케이스가 연속적으로 coalesce를 하지 않고 빠르게 할당을 진행하기 때문이다.

고찰 2. 그렇다면 오히려, 점수가 더 높아야 하는 것 아닌가?

thru는 만점이 40이고, 거의 모든 알고리즘에서 만점을 줄 정도로 점수가 비교적 후하다. 따라서 thru가 더 좋아도 만점에서 더 높아질 수는 없기에 점수가 더 높지는 않은 듯 하다.

B. Size-ordered - 사이즈 순 저장

// 적합한 가용 리스트를 찾아서 사이즈 오름차순에 맞게 현재 블록을 추가하는 함수
static void add_free_block(void *bp)
{
    int class = get_class(GET_SIZE(HDRP(bp)));
    void *currentp = GET_ROOT(class);
    if (currentp == NULL)
    {
        GET_ROOT(class) = bp;
        GET_SUCC(bp) = NULL;
        return;
    }

    while (GET_SIZE(HDRP(currentp)) < GET_SIZE(HDRP(bp)))
    {
        if (GET_SUCC(currentp) == NULL || GET_SIZE(HDRP(GET_SUCC(currentp))) > GET_SIZE(HDRP(bp)))
            break;
        currentp = GET_SUCC(currentp);
    }
    
    GET_SUCC(bp) = GET_SUCC(currentp);
    GET_SUCC(currentp) = bp;
    GET_PRED(bp) = currentp;

    if (GET_SUCC(bp) != NULL)
        GET_PRED(GET_SUCC(bp)) = bp;
}

사이즈를 기반으로 연결리스트에 블록을 넣어준다.

C. Address-ordered - 주소 순 저장

말 그대로 주소 순으로 연결리스트에 블록을 넣는다.

4. RBTree

저번 주에 rbtree를 구현하기도 했고, 카네기 멜런 대학의 CSAPP 강의에서 rbtree 방식도 있다는 내용을 듣고 흥미가 생겨서 구현에 도전했다.

하지만, 어떻게 블록을 노드로 하여 저장을 해야 할지, 부모와 자식에 대한 정보를 어떻게 저장해야 할지 등에 대한 발상에 어려움이 있었고, 구현 자체도 어려워서 결국 깃허브의 코드를 참고하여 그 코드를 이해하는 것을 목표로 하게 되었다.🥲

1) 메모리에 주소를 저장한다..!?

#define PARENT_BLK(bp)   (*(block_t*)((char *)(bp)))
#define LEFT_BLK(bp)  (*(block_t*)((((char*)(bp))+DSIZE)))
#define RIGHT_BLK(bp) (*(block_t*)((((char*)(bp))+2*DSIZE)))

블록의 값을 참조하면, 그 안에는 주소가 저장되어 있다. 즉, 메모리 주소에 다른 메모리 주소를 저장하는 방식이다.
그리고 이 저장된 주소를 캐스팅하여 포인터로 이용하여 탐색할 수 있다.

static void *find_fit_in_tree(size_t asize)
{
	block_t* bp;
	block_t* temp = NULL;
	bp = PARENT_BLK(heap_listp); //루트 노드
	while (bp != NULL) {
		if (GET_SIZE(HDRP(bp)) < asize) {
			bp = RIGHT_BLK(bp);
			continue;
		}
		if (GET_SIZE(HDRP(bp)) == asize) {
			temp = bp;
			tree_delete(temp);
			return temp;
		}

		else {
			temp = bp;
			if (bp != NULL) {
				bp = LEFT_BLK(bp);
				continue;
			}
			else
				break;

		}
	}

	if (temp != NULL){
		tree_delete(temp);
	}
	return temp; 
}

bp = LEFT_BLK(bp)코드에서 알 수 있듯, 메모리 주소에 접근하여 거기에 저장된 값(left child의 주소)을 다시 변수에 저장해가며 탐색을 수행한다.
더블 포인터를 사용하지 않기 위해 방식을 도입한 듯 한데 이렇게도 응용이 가능하다는 사실이 놀라웠다.

2) color bit

#define BLACK 0
#define RED 1
#define IS_RED(p) ((GET(HDRP(p))>>1)&0x1)

맨 뒤 비트는 allocate bit로 다른 알고리즘과 동일하다.
여기에 추가로 뒤에서 두번째 비트에 색깔 정보를 저장한다.
그리하여 현재 노드가 어떤 색깔인지 저장할 수 있게 된다.

if ((RIGHT_BLK(w) == NULL || !IS_RED(RIGHT_BLK(w))) && (LEFT_BLK(w) == NULL || !IS_RED(LEFT_BLK(w)))) {
	PUT(HDRP(w), PACK(GET_SIZE_ALLOC(HDRP(w)), RED << 1));
    PUT(FTRP(w), PACK(GET_SIZE_ALLOC(FTRP(w)), RED << 1));
    x = par;
    par = PARENT_BLK(par);
}

이런식으로 색깔을 바꿀 수 있다.

Appendix

inline function vs macro

"Inline function"과 "macro"는 프로그래밍에서 코드를 재사용하고 관리하기 위해 사용되는 두 가지 다른 메커니즘.

정의 방식과 처리 시점

Inline Function: 일반적인 함수와 유사하지만, 컴파일러에 의해 호출 지점에서 함수의 본문으로 대체되는 함수. 이는 컴파일 시점에 일어남.
Macro: 프로그램이 컴파일되기 전에 처리되는, 텍스트 기반의 치환 규칙. 매크로는 전처리기(preprocessor)에 의해 처리되며, 주로 C나 C++ 같은 언어에서 볼 수 있음.

타입 안전성

Inline Function: 함수이므로 타입 안전성을 제공. 즉, 인수의 타입이 체크되고, 오류가 발생할 수 있는 부적절한 사용을 방지할 수 있음.
Macro: 타입 체크가 없음. 매크로는 단순히 텍스트 치환을 수행하기 때문에, 타입 불일치로 인한 오류를 발생 가능성 존재.

디버깅

Inline Function: 일반 함수와 유사하게 디버그 가능. 오류 발생 시 추적이 용이.
Macro: 매크로는 디버깅이 어려움. 매크로는 컴파일 시간에 텍스트로 치환되며, 실행 중에는 원본 매크로의 형태로 보이지 않아 디버깅 시 혼란을 일으킬 수 있음.

성능

Inline Function과 Macro 모두 호출 오버헤드를 줄이기 위해 사용됨. 하지만, 인라인 함수는 컴파일러의 최적화에 따라 인라인 처리가 될 수도, 안 될 수도 있음.

재사용성과 유지보수

Inline Function: 일반 함수처럼 재사용성이 높고 유지보수가 용,
Macro: 매크로는 재사용성이 떨어지고 유지보수가 어려움. 특히, 크고 복잡한 매크로는 코드의 가독성을 떨어뜨릴 수 있음.
이러한 차이점들 때문에, 안전성과 유지보수의 용이성을 중시할 때는 인라인 함수를, 성능 최적화와 간단한 텍스트 치환을 필요로 할 때는 매크로를 선택하는 것이 일반적.