자유도와 카이제곱 분포

자유도의 개념

자유도는 주어진 통계 모델에서 독립적으로 변동할 수 있는 변수의 개수입니다. 간단히 말해, 모델에서 자유롭게 변화할 수 있는 정보의 양을 나타냅니다.

제약조건

자유도는 역설적으로 어떤 제약조건이 있기 때문에 사용하는 개념입니다. 그런 의미에서, 통계학에서 자유도는 제약조건을 정확하게 이해하기 위한 수단입니다.

통계량의 뜻

통계학에서, 통계량이란 확률변수들의 수식으로 표현이 가능한, 그리고 sample들로부터 계산이 가능한 확률변수입니다. 예를들어서, sample mean, sample variance는 그 자체로 확률변수이면서 또 sample들이 모두 주어져 있다는 가정하에 계산이 가능하기 때문에 통계량입니다.

Linear constraint and degree of freedom

확률변수 $n$개로 정의된 통계량을 계산하기 위해서는 Sample $n$개를 모두 알아야만 할까요?
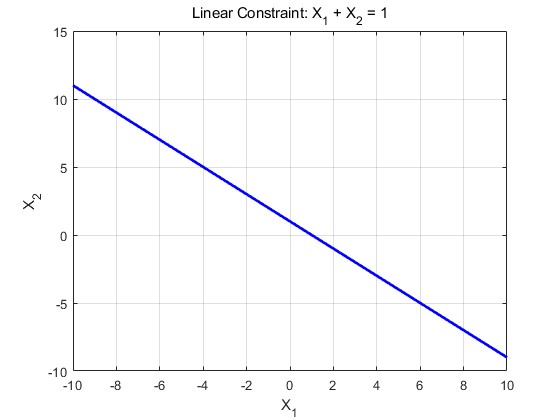
그렇지 않은 경우가 있습니다. 예를들어서, 확률변수 $X_1$, $X_2$에 대해서, $X_1 + X_2 =1$이라는 제약조건이 있는 경우, 다음과 같이 정의된 통계량 $T= X_1^2+X_2^2$을 계산하는 상황을 생각해봅시다. 이 경우, $T$를 계산하기 위해서는 사실 1개의 샘플만 있어도 충분합니다. 왜냐하면, 두 샘플이 서로에 대해서 종속적이니깐요.

In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.

특히, 자유도는 linear models을 공부하는데 매우 필수적인 개념입니다. 이 맥락에서는 다양한 통계량들이 선형대수학에서 말하는 벡터공간에 제약되는 확률벡터의 간단한 함수(선형함수 또는 2차형식)로 정의됩니다. 그리고 이 경우에는 그 통계량 계산의 자유도는 그 수식에 쓰인 확률벡터가 제약되는 선형공간의 차원으로 정의됩니다.

예를들어서, 위에서 예시로든 $T$는 확률벡터 $X=[X_1,X_2]$의 이차형식입니다. 그리고, 샘플 $X_1=x_1$, $X_2= x_2$가 주어질때, $x_1^2 + x_2^2$의 계산의 자유도는 1인데, 그 이유는 가능한 모든 $(x_1,x_2)$을 전부 모은 공간의 차원이 1이라서 그렇습니다.

카이제곱 분포

카이제곱 분포는 통계학에서 널리 사용되는 확률분포로, 주로 분산 추정, 독립성 검정, 적합도 검정 등에서 활용됩니다. 카이제곱 분포는 자유도에 따라 모양이 달라지는데, 자유도가 높을수록 정규분포와 비슷한 형태를 가지게 됩니다.

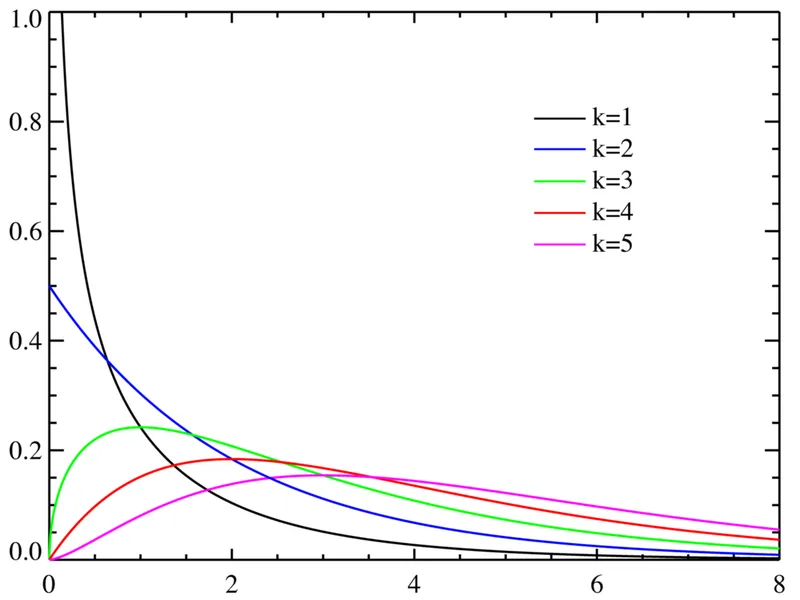
매개변수: 자유도(자연수) k

정규분포를 따르는 독립적인 확률 변수 $X_1, X_2, \ldots, X_n$에 대해, 각각의 값을 제곱하여 합산한 값을 카이제곱 통계량(Chi-Squared Statistic)이라고 합니다. 이 카이제곱 통계량은 카이제곱 분포를 따릅니다.

카이제곱 분포의 자유도

카이제곱 분포의 자유도는 카이제곱 통계량을 구성하는 독립적인 확률 변수의 개수에 의해 결정됩니다. 위에서 설명한 것처럼, 카이제곱 통계량은 정규분포를 따르는 확률 변수들을 제곱하여 합산한 것이므로, 독립적인 확률 변수의 개수와 일치하는 자유도를 가지게 됩니다.

따라서, $n$개의 독립적인 표준 정규분포를 따르는 확률 변수를 제곱하여 합산한 카이제곱 통계량의 자유도는 $n$입니다.

제약조건이 있는 카이제곱 통계량의 자유도

예를들어서, $X_1,\ldots,X_n$이 독립이고 동일한 정규분포$N(0,1)$를 따른다고 해봅시다. 그리고 $\bar{X}$가 $X=[X_1,\ldots,X_n]$의 산술 평균이라 합시다. 그리고 다음과 같이 통계량 $T$(표본분산 × ($n-1$)) 를 정의합시다.

$X_1,\ldots,X_n$이 동일한 정규분포 $N(0,1)$를 따른다는 가정에 의해서,

$T=Y_1^2 + Y_2^2 + \ldots + Y_n^2$는 자유도가 $n-1$인 카이제곱분포를 따릅니다.

표본분산의 자유도가 $n-1$인 이유

확률벡터를 구성하는 독립적인 변수 $X_i$의 개수는 $n$개 입니다. 그러면, $T$의 자유도가 $n$입니까? 아닙니다. 사실, $T$의 자유도가 $n$일 수 없다는 것을 직관적으로 이해하는것이 정말 중요합니다.

간단히 설명하자면, $\sum_{i=1}^n ( X_i - \overline{X}) =0$이기 때문입니다. 그러니깐
$X_1 - \overline{X}$ 부터 $X_{n-1} - \overline{X}$의 sample들이 주어지면, 자동으로 마지막 변수인 $X_n - \overline{X}$의 sample이 결정되겠지요. 그래서 애초에 $X_i - \overline{X}$들은 잉여정보를 하나 가지고 있고, 이들 중 하나가 빠지더라도 $T$를 계산하는데 문제가 없으므로 $T$의 자유도는 $n-1$ 이하입니다.

여기서, $T$는 확률변수 $X_i - \overline{X}$의 제곱합으로 주어지므로,
$Y_i = X_i-\bar{X}$라 정의하겠습니다. 최종적인 수식은
$T= Y_1^2 + Y_2^2 + \ldots + Y_n^2$으로 주어지고, 확률벡터
$Y = [Y_1,\ldots,Y_n]$의 linear constraint는 다음과 같습니다.
$Y_1 + \ldots + Y_n = 0$.

$X_i$들을 기준으로 수식을 보면, 그 수식이 제곱합이 아니므로, 확률벡터 $X$가 아니라, $Y$를 기준으로 자유도를 계산해야합니다.

사실, 자유도가 정확히 $n-1$임이 알려져 있고, 직관적인 설명을 다음과 같습니다.
$T$는 $n$개의 확률 변수 $Y_i$의 제곱합으로 구성되지만, 제약조건 $Y_1 + Y_2 + \ldots + Y_n = 0$을 고려할 때, 실제로는 $n-1$개의 독립적인 정보만을 포함하고 있습니다. 다시말해서, $n$에서 제약조건의 개수 (1)을 빼서, 자유도 $n-1$을 구할 수 있습니다.

수학적인 설명은 다음과 같습니다. $Y$는 모든 성분이 1로 구성된 행렬 $J$를 이용해서, 다음과 같이 나타낼 수 있습니다. (아래의 수식에서, $X$, $Y$는 각각 $X_i$, $Y_i$로 구성된 열벡터라고 합시다.)
$Y = \left(I-\frac{1}{n}J\right)X$
여기서, 행렬 $\left(I-\frac{1}{n}J\right)$의 rank을 구하면 $n-1$이므로, $Y$의 값들로 구성된 공간의 차원도 $n-1$입니다. 따라서, 자유도는 $n-1$입니다.

정리하자면,

• 모든 성분이 1로 구성된 행렬 $J$에 대해서
  $Y = \left(I-\frac{1}{n}J\right)X$ 입니다.
• 행렬 $I-\frac{1}{n}J$의 대각합이 $n-1$입니다.
• 또한 이 행렬은 멱등 행렬이므로 : $(I-\frac{1}{n}J)^2=I-\frac{1}{n}J$, 이 행렬의 rank도 $n-1$입니다.
• 따라서, $T$의 자유도는 $n-1$입니다.

카이제곱 분포를 따르는 이유

결론부터 말하자면, $T= Z_1^2 + Z_2^2 + \ldots + Z_{n-1}^2$으로 적을 수 있습니다. 단, $Z_i$는 서로 독립이고 동일한 정규분포 $N(0,1)$을 따릅니다. 그렇다면, 그러한 $Z_i$들의 존재성은 어떻게 증명할 수 있을까요?

증명에 필요한 재료들

스펙트럴 정리의 특수한 경우

$A$가 대칭행렬이면서 멱등행렬이면, 다음과 같은 형태로 분해가 가능합니다.
$A=\sum_{i=1}^r \bold u_i \bold u_i ^\top$, $r=\text{rank} \ A$ 그리고 $\bold u_i$는 $A$의 열공간 $\text{col}(A)$의 정규직교기저를 이룸.

다변량 정규분포의 뜻과 covariance 행렬 계산법

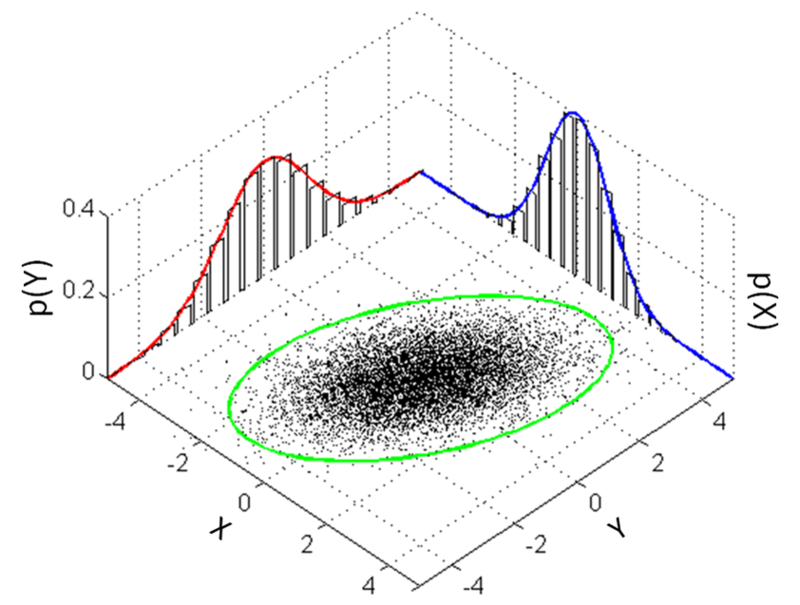
만약 확률벡터 $X=[X_1, X_2, \ldots, X_n]$의 모든 선형결합$a_1X_1 + a_2X_2 + \ldots + a_nX_n$이 일변량 정규분포를 따르면, $X$가 다변량 정규분포를 따른다고 말합니다.

$Z$를 $n$차원 확률벡터로 이고, 그 성분들이 서로 독립이고 각각 $\mathcal{N}(0,1)$ 분포를 따른다고 합시다. 그러면, $Z$는 다변량 정규분포를 따릅니다. 게다가, 행렬 $A$와 열벡터 $b$에 대해서 다음이 성립합니다. (단, 밑의 수식에서 행렬곱과 합이 정의 될때에)

다변량 정규분포의 독립성에 대한 정리

만약, 확률벡터 $Z=[Z_1,\ldots,Z_n]$가 다변량 정규분포를 따르면 다음 두 문장이 동치입니다.

• $Z_1, Z_2, \ldots, Z_n$ 은 독립입니다.
• $Z$의 covariance 행렬 $\text{Cov} \ Z$은 대각행렬입니다.

증명 아웃라인

$A=I-\frac{1}{n}J$라 합시다. 그러면 $Y=AX$입니다. 의미를 말하자면 , $X$는 제약조건이 없는 랜덤벡터이고 $Y$는 제약조건이 있는 랜덤벡터입니다. 다시한번 강조하는데, $Y$의 자유도는 rank $A$ 즉 $n-1$입니다.

우리의 목적은 $Y$의 분포가 카이제곱분포를 따름을 보이는 것입니다. (자유도는 이미 보였으니까요)

• 다음을 만족시키는 $\text{col}(I-\frac{1}{n}J)$의 정규 직교기저 $\{\bold u_1,\ldots,\bold u_{n-1}\}$이 존재합니다. (기저의 원소개수가 $n-1$인 이유는 행렬의 rank가 $n-1$이라 그렇습니다.)
  $A=\sum_{i=1}^r \bold u_i \bold u_i ^\top$, $r=\text{rank} \ A$ 그리고 $\bold u_i$는 $A$의 열공간 $\text{col}(I-\frac{1}{n}J)$의 정규직교기저를 이룸.

• $Z_i = \bold u_i \cdot \bold X$라하면, $T=\sum_{i=1}^{n-1} Z_i^2$이다. 왜냐하면,

  $T =\sum_{i=1}^{n}Y_i^2 = Y^\top Y = [AX]^\top [AX] = X^\top A^\top A X = X^\top A X = \sum_{i=1}^{n-1} [u_i^\top X]^\top[u_i^\top X].$

• $\{\bold u_1,\ldots,\bold u_{n-1}\}$가 정규직교기저이므로, 위에서 정의한 $Z_i$의 집합이 통계적으로 독립입니다. 왜냐하면, $U^\top$를 $\bold u_i^\top$을 행으로 쌓아서 얻은 행렬이라 할때 $Z = U^\top X$이고, $Z$의 covariance matrix는 단위행렬 $\text{cov} \ Z = U^\top U = I$이기 때문입니다.