예측(prediction)과 회귀(regression)

• 특정한 입력변수값을 사용하여 출력변수의 값을 계산하는 문제
• 예측문제 중에서 출력변수의 값이 연속값인 문제를 회귀(regression) or 회귀분석(regression analysis)라고 한다.

회귀분석

독립변수에 따른 평균 반응값을 추정, 예측하는 모형

• 목적 : 두 변수 사이의 선형성이 존재한다는 가정하에 그 선형관계를 대표할 수 있는 하나의 직선(모형)을 구하고, 새로운 값에 대한 반응값을 예측

• 분산분석과 회귀분석은 선형모형이라는 큰 줄기에서 같은 방법론이지만, 독립변수가 연속형(수치형)인 경우에 사용된다.

  종속변수 (반응변수)	독립변수(설명변수)	통계분석법
  수치형	범주형(3개 이상)	분산분석(ANOVA)
  수치형	수치형	회귀분석

회귀분석의 종류

• 독립변수와 종속변수의 수 : 단순 회귀분석, 다중회귀분석 등
• 독립변수와 종속변수의 관계 : 선형 회귀분석, 다항 회귀분석(비선형 회귀분석) 등

선형회귀분석

두 변수 사이의 선형성이 존재한다는 가정하에 그 선형관계를 대표할 수 있는 하나의 직선(모형)을 구할 때, 관찰치$X,Y$가 주어졌을 때 그 관계를 표현하는 $a,b$를 어떻게 추정해야 가장 효율적이고 변수간의 관계를 정확히 나타낼 수 있는 지를 이해하는 것이 중요하다.

최소제곱추정법

method of least squares estimation
잔차의 제곱합을 최소로 만들어주는 $a,b$ 를 추정하는 방법이다.
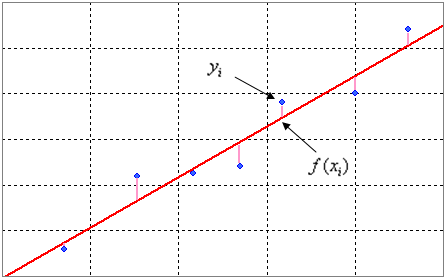잔차(residual) 는 실제 관측값과 예측된 값의 차이를 뜻하고, 그 제곱합을 최소로 한다는 것은 해당 선과 실제 관측값의 차이의 총량을 최소로 하겠다는 것을 의미한다.

회귀 모형의 유의성 검정

자유도
자유롭게 선택될 수 있는 자료의 수를 의미하는데, 온전히 해당 통계량에 대한 정보를 생성하는 데 사용되는 자료 수이다.

• 관측치가 2개일 때 단순회귀분석의 경우 회귀선이 두 점을 지나야한다. 이 경우 두 선을 지나는 회귀선을 추정할 수는 있지만 평가할 자유도(관측치)는 없다. 관측치가 3개면 회귀제곱합$SSR$의 자유도가 2, 잔차제곱합$SSE$의 자유도가 3-2=1이 된다.
• 독립변수가 2개 이상인 다중회귀분석의 경우, 3차원 좌표 공간에서 면으로 표현할 수 있으므로 최소한 3개의 점이 필요하다. 관측치가 최소한 4개 이상이어야 회귀식을 평가할 수 있다는 것이다.

즉, $SSR$의 자유도는 독립변수의 수, $SSE$의 자유도는 관측치(표본) 개수 - 독립변수 개수-1 이다.

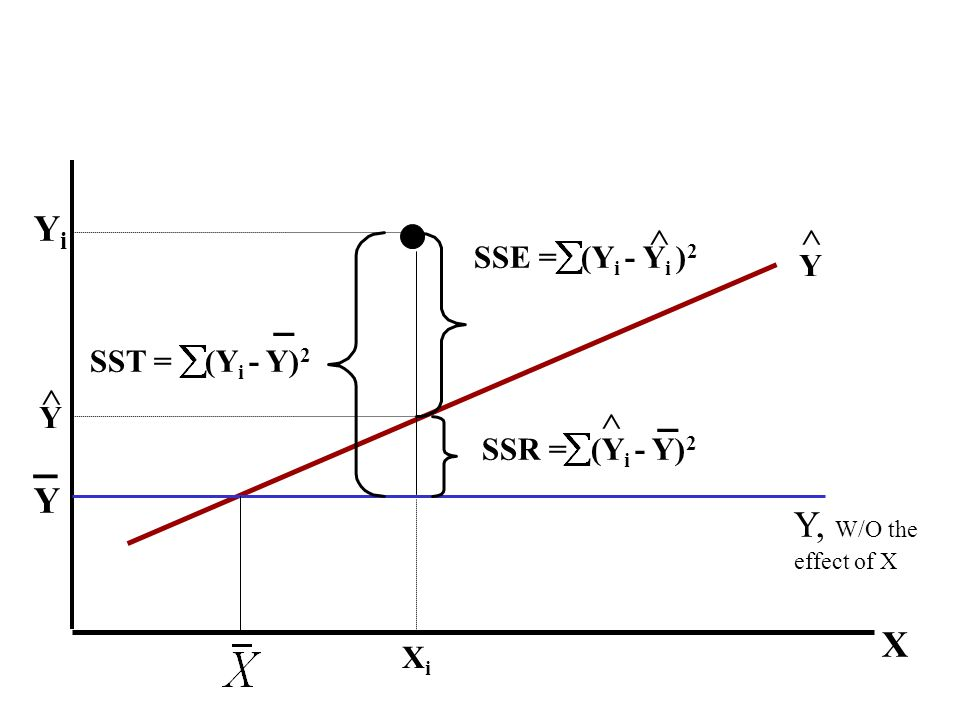
결정계수 $R^2$
coefficient of determination, 전체 변동중 회귀선에 의해 설명되는 변동이 차지하는 비중을 뜻한다.
$R^2 = \frac {SSR} {SST} = 1- \frac {SSE} { SST}$

회귀식 유의성 검정

$H_0$ : 추정된 회귀식은 유의하지않다
$H_1$ : 추정된 회귀식은 유의하다

$F_0=\frac {SSR/df_R } { SSE/df_E} =$ $MSR \over MSE$ $\sim F (df_R,df_E)$

$df_R=k ,\ df_E=n-k-1, \\ n:number;of\; observations \\ k:number\;of\;predictors$

• 회귀식으로 설명되는 변동(MSR)이 큰 경우 $F0$은 큰 값을 가지고, 귀무가설을 기각한다. (추정된 회귀식은 유의하다)

회귀모형 설정

회귀모형
$Y_{i}=\beta_{0} +\beta_{1}x_{i}+\epsilon_{i}, \ \epsilon_{i} \sim iidN(0,\sigma^{2})$

• $\epsilon_{i} \sim iidN(0,\sigma^{2})$
  X값은 주어진 값으로 오차항의 분포가 종속변수 Y의 분포이다. 따라서 오차항에 대한 가정 독립성, 정규성, 등분산성 세가지도 만족해야한다.

추정된 회귀식
$\hat Y_i = b_0 + b_1 X_i$

• $b_1$
  • 양/음, 절댓값 크기에 따른 종속변수 Y에 대한 X의 영향을 파악할 수 있다.
  • 회귀계수 유의성 검정(기울기 검정)은 $t$분포를 이용한다. 위의 회귀모형 설정에서 정규성 가정이 만족하는 경우, 회귀꼐수가 t분포를 따르기 때문이다.
    • $H_0:\beta_1=0$
    • $H_1:\beta_1\neq0$

선형 회귀 분석 결과 해석(python)

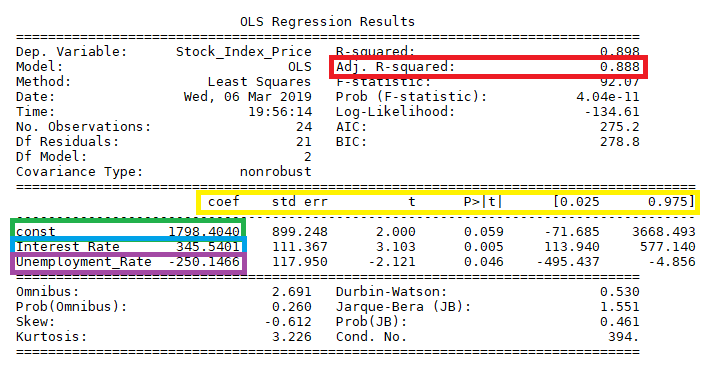
OLS Regression Results

Ordinary Least Squares 는 앞서 살펴본 최소제곱법과 동일한 의미이다.

• no.obs : 표본 수
• Df Residuals : 잔차의 자유도 (전체 표본 수에서 측정되는 변수들의 개수를 뺀 것: 표본 수 - 종속변수개수-독립변수개수)
• Df Model : 독립변수 개수
• R-Squared : 결정계수($SSR\over SST$), 회귀모형의 설명력, 전체 데이터 중 회귀모형이 설명할 수 있는 데이터의 비율(1에 가까울 수록 성능이 좋음)
• Adj.R-Squared : 데이터에 따라 조정된 결정 계수
• F-statistics : F 통계량($MSR \over MSE$), 0에 가까울수록 적절
• Prob(F-statistics) : 0.05 이하인 경우 회귀식 유의미
• 조정결정계수
  독립변수 p가 많은 모델이면 RSS는 작아지게 된다. AIC, BIC를 최소화하는 것은 우도를 가장 크게 만드는 동시에 변수의 개수는 가장 최적의 모델을 의미한다. Bias 는 변수를 제거해서 생기는 오류, variance는 변수가 증가하면서 생기는 오류로 둘의 trade off 관계에서 AIC와 BIC는 최적의 모델 선택을 위한 균형점을 제시한다.
  • AIC (Akaike Information Criterion)
    $-2Log(Likelihood) + 2p$
    AIC가 작을수록 모형이 실제 자료의 분포와 유사하다.
  • BIC (Bayesian Information Criterion)
    $-2Log(Likelihood) + log(n)p$
    BIC가 작을수록 예측력이 좋음

• coef : 회귀계수
• std err : 계수 추정치의 표준오차
• t : t 통계량, 독립변수와 종속변수 사이의 상관관계로 값이 클수록 상관도가 큼
• p-value (P>|t|) : 독립변수의 유의확률(유의수준 0.05일 때 0.05보다 작을 때 유의미하다고 할 수 있다.)
• [0.025 0.0975] : 유의수준 0.05일 때 회귀계수의 신뢰구간
• skew : 왜도 평균 주위의 잔차들이 대칭하는 지, 0에 가까울수록 대칭
• kurtosis : 첨도 잔차들의 분포 모양으로, 3에 가까울 수록 정규분포, 음수일 경우 평평, 양수일 경우 뾰족 형태

다중공선성 multicollinearity

Cond. No.,Warnings [2]
상관관계가 높은 독립변수들이 모델에 포함될 때 발생하고 다중공선성이 높으면 회귀계수의 표준오차가 커지게 된다.

• $t$ 값에 의해 회귀계수의 유의성을 계산하는데 표준오차가 비정상적으로 커지면 $t$ 값이 작아지고 p-value값이 커져서 유의하지 않다는 잘못된 결론에 도달할 수 있다.
• Cond. No는 상태지수Condition Index로, 10이상이면 다중공선성이 크다고 판단할 수 있다.
• 다중공선성을 해결하기 위해서는 다중공선성이 큰 변수의 유의성 검증을 수행하하거나, 해당변수를 제거, PCA를 통해 변수를 재조합하여 겹치는 분산을 제거하는 등의 방법이 있다.

---

Reference & Source
단순선형회귀분석의 추정
statsmodel-linearregression
변수선택법
회귀모형해석