해당 글은 강화 학습의 개념 전반에 대해 순차적으로 다룰 예정입니다.

이번 포스팅에서는 에피소드의 종료를 기다리지 않고 모델을 업데이트하는 Temporal Difference 모델에 대해 다루겠습니다.

Temporal Difference Algorithm

Temporal Difference Algorithm은 에피소드의 종료를 기다리지 않고 가치 함수를 업데이트할 수 있는 model-free 알고리즘이다.

Monte Carlo 알고리즘은 MDP에 대한 정보 ($R_s^a, P_{ss'}^a$)를 알지 못하는 model-free한 상황에서, 동작이 완료된 에피소드들을 사용해 가치 함수를 업데이트하면서 최적 정책을 찾는 방법이었다. 하지만 MC의 경우 에피소드가 종료되기 전에는 모델을 업데이트할 수 없다는 단점이 존재한다. 또한 각 상태의 가치를 업데이트하기 위해 해당 상태에서의 리턴이 필요하기 때문에 이 과정을 효율적으로 수행하기 위해 에피소드의 역순으로 상태를 업데이트해야 한다는 제한사항도 존재한다. 이러한 문제를 해결하기 위해 제시된 것이 Temproal Difference 모델이다.

Temporal Difference(TD) 알고리즘은 MC와 마찬가지로 MDP에 대한 정보를 알지 못하는 model-free 알고리즘으로, 아래 식처럼 에피소드의 종료를 기다리지 않고 모델을 업데이트하기 위해 다음 상태의 가치와 그 상태로 넘어갈 때 받은 보상값으로 리턴을 대신하는 방식이다.

$G_t = R_{t+1} + \gamma V(S_{t+1})$

따라서 이 식을 MC 알고리즘에서 사용했던 식 $V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t))$에 대입하면 다음과 같이 나타낼 수 있다.

$V(S_t) \leftarrow V(S_t) + \alpha(R_{t+1}+\gamma V(S_{t+1})-V(S_t))$

이 때, $R_{t+1}+\gamma V(S_{t+1})$을 TD target이라고 부르며, TD target - $V(S_t)$를 TD error라고 한다. 결국 TD 알고리즘의 목표는 이 TD error을 최소화 하는 방향으로 학습을 진행하는 것이다.

TD 알고리즘을 사용해 학습을 할 때에는, 일반적으로 transit을 $(s, a, r, s')$의 4가지 항으로 선택하게 된다. 이는 $s$ 상태에서의 가치를 업데이트할 때 다음 상태 $s'$가 어떤 상태인지 알아야 $V(s')$을 통해 $V(s)$를 업데이트할 수 있기 때문이다.

Adventages of TD

그렇다면 이제 에피소드의 종료를 기다리지 않고 학습을 진행하는 것이 왜 장점이 되는지 생각해보자.

지금까지 예시로 든 small grid world 등의 간단한 환경에서는 에피소드가 소수의 상태를 거치는 것으로 종료되기 때문에 큰 차이가 없지만, 실제 환경에서 강화 학습을 수행하기 위해서는 수십, 수백 개의 transit으로 이루어진 에피소드를 통해 학습을 진행해야 하는 경우가 빈번히 발생한다. 이러한 에피소드를 수만, 수십만 번 학습시켜야 경쟁력 있는 강화학습 모델을 완성할 수 있는 것이다. 그런데 그 정도 양의 에피소드를 전부 하나하나 종료될 때까지 기다렸다가 학습을 진행한다면 학습에 걸리는 시간이 기하급수적으로 늘어날 수밖에 없는 것이다. 그렇기 때문에 TD의 구조가 실제 환경에서 활용하기에 훨씬 효율적인 것이다.

Bias/Variance Trade-Off

Bias는 편차로 sample들이 정답에서 얼마나 한 쪽으로 치우쳐 있는지 나타내는 값이고, Variance는 분산으로 sample들이 얼마나 넓게 분포해 있는지 나타내는 값이다.

우리가 학습한 MC와 TD는 모두 에러를 최소화하는 방향으로 학습을 진행하는 모델들이다. 이 때, 우리가 말하는 에러는 noise, bias, variance의 합으로 계산할 수 있다. 여기서 noise는 완전히 없애기 어렵기 때문에 우리는 bias와 variance의 합이 최소가 될 수 있도록 환경에 맞춰 모델을 선택해야 하는 것이다. 그렇다면 MC와 TD의 bias와 variance는 어떻게 분포해 있을까?

우선 MC의 경우, 종료된 에피소드의 결과를 이용해야 하기 때문에 sample이 매우 많이 사용된다. 또한 MC에서의 가치 함수는 리턴의 기댓값을 통해 업데이트되기 때문에 sample이 늘어날수록 그 평균은 최적 가치에 수렴하게 된다. 따라서 MC는 unbias한 모델이라는 것을 추론해낼 수 있다. Variance도 리턴에 영향을 받는데, 결국 리턴은 확률적인 요소를 포함하기 때문에 실제로 특정 에피소드를 수행했을 때 획득하는 리턴이 100이 될수도, -100이 될수도 있는 것이다. 이러한 확률적인 오차를 줄이기 위해서 기댓값을 사용하는 것이기 때문에, 기댓값은 최적 가치에 수렴한다 하더라도 각각의 sample은 최적 가치와 차이가 날 수 있는 것이다. 따라서 MC의 variance는 크다는 것을 예상할 수 있다.

반면 TD의 경우는 특정 상태에서의 가치를 계산할 때 다음 상태의 가치가 영향을 주기 때문에, 가장 마지막 상태가 정확하지 않으면 해당 상태를 기반으로 업데이트한 앞의 상태들도 전부 부정확한 값을 이용해 업데이트되기 때문에 bias가 커지게 된다. 반면 TD를 학습할 때에는 시점 $t$에서의 가치 $V(S_t)$를 업데이트할 때 다음 시점에서의 가치 $V(S_{t+1})$만 사용하기 때문에 수많은 sample의 리턴의 기댓값으로 업데이트를 진행하는 MC보다 variance는 더 작을 것이기 때문에, 결과적으로 TD는 bias가 크고, variance가 작은 모델이라는 것을 알 수 있다.

이처럼 MC와 TD는 bias와 variance간의 trade-off를 가지고 있는데, 실제로 둘 중에서 강화학습에 주로 사용하는 모델은 TD이다. 그 이유는 최적해를 찾는 과정에서 bias보다 variance의 영향력이 더 크기 때문이다. Variance가 크다는 것은 그만큼 sample들이 넓은 영역에 분포해있다는 것이기 때문에 sample들 간의 오차가 클 수밖에 없다. 물론 sample이 무작위로 생성되는 만큼 sample의 수가 늘어나면 점차 정규분포에 가까운 형태로 sample이 분포되어 최종적으로는 그 기댓값이 최적해에 가까워지겠지만, 그 정도 양의 에피소드 sample을 생성하여 각각의 에피소드가 종료될 때까지 기다리면서 순차적으로 policy evaluation을 하면 요구되는 연산량이나 시간이 기하급수적으로 늘어날 것이다. 반면 bias의 경우는 최적해에서 떨어진 만큼 sample들을 translation 해주면 최적해 근처에 분포해있는 것처럼 사용할 수 있기 때문에 bias의 값은 학습에 크게 영향을 주지 않는다. 따라서 이러한 차이 때문에 model-free한 강화학습 모델 중에서는 Temporal Difference가 선호되는 것이다.

Example using Batch Learning

아래와 같이 유한한 에피소드가 주어져있고, 이 에피소드들을 이용해 batch 방식으로 학습을 진행한다고 생각하자. 그렇다면 각각의 상황에서 MC와 TD는 가치 함수를 각각 어떻게 계산할까?

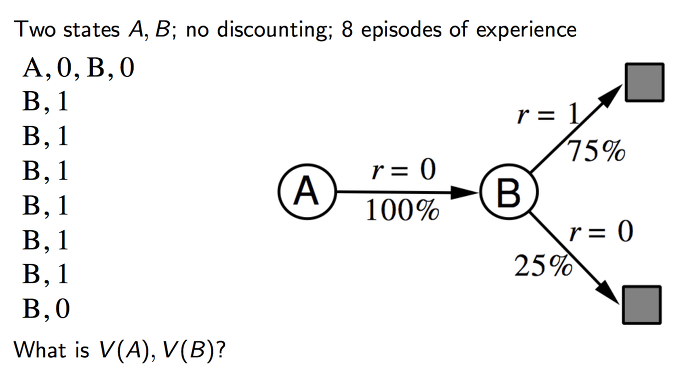
Monte Carlo

MC는 각각의 에피소드의 결과를 기반으로 가치 함수를 업데이트하기 때문에, 주어진 에피소드를 통해 MC에서의 $V(A)=0$ 이라는 사실을 확인할 수 있다. 또한 $B$ 상태에서는 리턴이 1인 에피소드가 6번, 0인 에피소드가 2번 존재했기 때문에 $V(B)=6/8=0.75$ 이다.

Temporal Difference

TD에서는 $V(A)=R_A + V(B)$로 나타낼 수 있기 때문에, 학습을 반복하면서 업데이트된 $V(B)$가 $V(A)$에도 영향을 준다. 모든 에피소드에서 $V(B)$는 마지막 상태이기 때문에 $V(B)$는 MC와 마찬가지로 0.75임을 알 수 있다. 따라서 $V(A)=R_A + 0.75$를 성립하게 되는데, $R_A=0$ 이므로 최종적인 $V(A)=0.75$가 된다.

즉, MC와 TD에서의 $V(A)$는 각각 0, 0.75임을 확인할 수 있다. 이러한 차이가 발생하는 것은 TD에 MDP의 특징이 반영되어 있으나, MC에는 이러한 특징이 반영되지 않았기 때문이다. TD는 $V(S_t)$의 값을 업데이트하기 위해 $R_{t+1}+V(S_{t+1})$라는 추정치를 사용하는 bootstrapping 방식을 사용하나, MC는 단순히 연속적인 transit의 sample을 토대로 학습을 진행하는 방식이기 때문이다. (TD와 MC 모두 sample를 기반으로 업데이트를 진행하는 sampling 모델이지만, bootstrapping의 여부에 따라 차이가 나는 것이다.) 따라서 Markov 환경에서는 TD가 훨씬 효율적으로 사용될 수 있는 것이다. 반면 Markov 환경이 아닌 경우에는 이웃한 상태 간의 관계를 통해 가치 함수를 계산할 수 없기 때문에 sampling 방식의 MC를 더 효율적으로 사용할 수 있다.

Additional Issue (backup method)

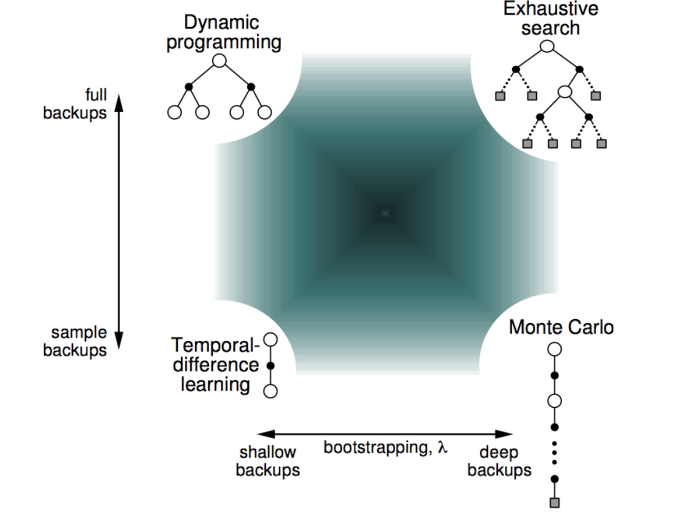
해당 그림은 bootstrapping 여부와 backup 방식에 따른 사용 가능한 모델을 나타낸 것이다. DP와 Exhaustive search는 모든 case를 전부 계산하여 업데이트를 진행하는 full backup 방식을 사용하나, TD와 MC는 model-free 방식을 사용하기 때문에 추출한 일부 sample을 통해 업데이트를 진행하는 sample backup을 사용한다. 한편, DP와 TD는 모두 bootstrapping 방식을 사용하du 바로 다음 단계의 정보만 알고 있으면 업데이트를 진행할 수 있기 때문에 shallow backup 방식을 사용하며 MDP 모델에서 사용할 수 있다. 하지만 bootstrapping 방식을 사용하지 않는 Exhaustive search와 MC는 goal에 도달한 에피소드를 사용해서 업데이트를 진행해야 하기 때문에 deep backup 방식을 사용한다.

n-Step Temporal Difference

우리가 TD를 사용하는 이유는 $t$에서의 상태 $S_t$보다 goal에 가까운 $S_{t+1}$의 불확실성이 더 낮다는 판단에 의한 것이다. 여기서 더 관점을 확장하여, $t$보다 $n$단계 뒤에 존재하는, $t+1$보다 더 불확실성이 낮은 $S_{t+n}$에서의 가치를 사용해 $V(S_t)$를 업데이트한다는 발상에서 만들어진 것이 바로 n-Step TD이다. n-Step TD에서의 리턴과 가치함수를 식으로 나타내면 다음과 같다.

$G_t^{(n)}=R_{t+1}+ \gamma R_{t+2} + ... + \gamma^{n-1}R_{t+n} + \gamma^nV(S_{t+n})\\ V(S_t) \leftarrow V(S_t) + \alpha (G_t^{(n)}-V(S_t))$

결국, n-Step TD에서 $n=1$인 경우를 우리가 배웠던 TD, $n=\infin$인 경우를 MC라고 할 수 있는 것이다. 이러한 n-Step TD를 사용하는 이유는 앞서 말했던 불확실성의 감소 뿐만 아니라 TD와 MC의 특징을 골고루 가지게 되면서 TD의 bias 이슈와 MC의 Variance 이슈를 함께 감소시킬 수 있기 때문이다.

TD(λ)

결국 n-Step TD에 따르면 $t+1$부터 goal 까지의 모든 상태의 가치는 TD target(리턴)이 될 수 있다. 또한 최적 정책은 TD error (TD target - $V(S_t)$)가 0이 되어야 하기 때문에, 최적 정책에서 모든 $n$에 대해 n-Step TD의 리턴 $G_t^{(n)}$는 같은 값을 가져야 한다. 하지만 실제로 학습을 진행할 때에는 n의 값에 따라 $G_t^{(n)}$이 달라지는 문제가 발생하게 된다. 이 문제를 해결하기 위해, 학습에 사용할 TD target으로 가능한 모든 $n$에 대한 리턴 $G_t^{(n)}$의 기댓값 사용하기로 했고, 그렇게 계산한 기댓값을 $\lambda$-return이라고 부른다. $\lambda$-return $G_t^\lambda$는 다음과 같이 나타낼 수 있다.

$G_t^\lambda = (1-\lambda)\sum_{n=1}^\infin \lambda^{n-1}G_t^{(n)}$

이 때, $\lambda$는 멀리 떨어진 단계의 가치 함수를 업데이트에 사용하는 것에 따른 가중치이다. $1-\lambda$가 식에 곱해진 것은 $\sum \lambda^{n-1}$의 합이 ${1} \over {1-\lambda}$이기 때문에, $G_t^{(n)}$의 기댓값을 계산하기 위해 곱해준 것이다.

하지만 우리가 실제로 학습을 진행하는 환경은 $n \rightarrow \infin$로 발산하는 환경이 아니다. 따라서 시점 $t$가 유한한 값 $T$로 수렴하는 경우에 대한 $\lambda$-return을 고려해야 한다. 아래 그림은 기존의 $\lambda$-return에서의 가중치 $(1-\lambda)\lambda^{n-1}$의 함수 그래프로, 해당 함수가 지수 함수의 형태를 띄고 있으며 전체 면적의 합이 1이라는 것을 알 수 있다. 하지만 $T$가 유한한 경우, 가중치의 총합이 1이 아니기 때문에 실질적인 $G_t^\lambda$의 값은 감소하게 된다.

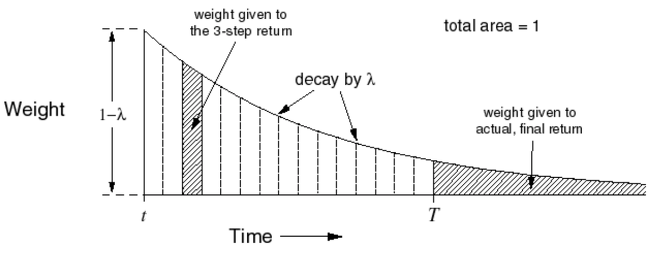
따라서 이 때의 오차를 보정하기 위해 시점이 유한한 경우 아래와 같이 $\lambda$-return을 나타낼 수 있다. 해당 식에서 추가된 $\lambda ^{T-t-1}G_t$ 항을 통해 현재 값을 보정해주는 것이다.

$G_t^\lambda = (1-\lambda) \sum_{n=1} ^{T-t-1}\lambda^{n-1}G_{t:t+n} + \lambda^{T-t-1}G_t$

결과적으로 다음과 같이 $\lambda$-return을 계산하여 학습한 TD를 TD($\lambda$)라고 부른다. TD($\lambda$)의 가치 함수를 식으로 나타내면 다음과 같다.

$V(S_t) \leftarrow V(S_t) + \alpha(G_t^\lambda-V(S_t))$

Backward-View TD(λ)

TD($\lambda$)도 지금까지 설명한 다른 유형의 TD와 마찬가지로 기본적으로 미래의 상태를 통해 현재 상태의 가치를 업데이트하는 방식을 사용한다. 이를 Forward-view TD($\lambda$)라고 한다. 하지만 TD($\lambda$)는 MC와 마찬가지로 에피소드 상의 모든 리턴을 알아야 업데이트가 가능하기 때문에 종료된 에피소드에 대해서만 학습이 가능하다는 단점이 존재한다. 이 문제를 해결하기 위해 나온 것이 Backward-View TD($\lambda$)이다.

Backward-View TD($\lambda$)를 설명하기 전에 우선 Eligibility Trace에 대해 알아보자. Eligibility Trace는 특정 액션이 동작한 것에 무엇이 영향을 주었는지 고려하기 위한 개념이다. 이 때 고려해야 할 것은 해당 상태가 얼마나 많이 발생했는지(Frequency Heuristic)와 얼마나 최근에 발생했는지(Recency Heuristic)이다. 이 두 가지를 결합하여 과거 시점의 상태를 업데이트하는 것이 바로 Eligibility Trace이다. Eligibility Trace에 의한 가중치 $e_t(s)$는 다음과 같이 나타낼 수 있다.

$e_t(s)= \Bigg\{{\gamma \lambda e_{t-1}(s)\ \ \ \ \ \ \ \ \ \ \ if\ s\neq s_t \atop \gamma \lambda e_{t-1}(s)+1 \ \ \ \ if \ s= s_t}$

식에 따르면, $\gamma$와 $\lambda$는 어차피 [0, 1] 사이의 값이므로 상태 $s$가 나오지 않을수록 $e_t(s)$의 값은 감소하게 된다. 하지만 상태 $s$가 근래의 시점에 나오거나 여러 번 반복해서 나오게 되면 $e_t(s)$의 값이 점점 커진다는 것을 알 수 있다. 따라서 이러한 Eligibility Trace의 과정을 거친 가중치를 이용하여 모든 상태 $s$에 대한 가치를 업데이트하는 것이다. 업데이트는 TD Error $\delta_t$와 Eligibility Trace Discount $e_t(s)$, 그리고 learning late $\alpha$를 사용해 아래 식처럼 진행된다.

$V(s) \leftarrow V(s) + \alpha \delta_t e_t(s)$

따라서 Backward-View TD($\lambda$) 방식을 사용하게 되면 Forward-View TD($\lambda$)처럼 $\lambda$-return을 계산하는 대신 Eligibility Trace Discount와 TD Error을 사용해서 가치 함수를 업데이트할 수 있는 것이다. 이 경우에는 과거의 상태를 사용해서 가치를 업데이트하기 때문에 종료된 에피소드를 사용해서 업데이트를 수행해야 하는 Forward-View TD($\lambda$)보다 효율적으로 업데이트를 수행할 수 있다.

Additionals

• 다음 그림은 Eligibility Trace Discount인 $e_t(s)$를 그래프로 나타낸 것이다.

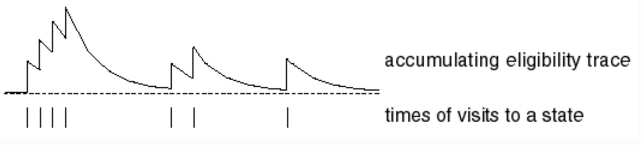
• TD(0)은 우리가 처음 배웠던 기본적인 형태의 TD와 동일하다. Backward-View TD($\lambda$)에서 $\lambda=0$을 대입하면 $e_t(s)$가 0또는 1의 값을 가지기 때문에 $V(S_t) \leftarrow V(S_t) + \alpha \delta_t$로 정리되어 기본적인 TD와 같아지는 것이다.