
1. 연결 리스트의 개념적인 이해
'연결 기반의 리스트' 간단히 '연결 리스트'라 불리는 리스트의 구현을 이해하기 위해서는 'malloc함수와 free함수를 기반으로 하는 메모리의 동적 할당'에 대한 완전한 이해가 선행되어야 한다.
그럼 다음 예제를 시작으로 '연결 리스트'에서의 '연결'이 의미하는 바의 설명을 진행하겠다.
ArrayRead.c
#include <stdio.h>
int main(void)
{
int arr[5];
int readCount = 0;
int readData;
int i;
while(1)
{
printf("자연수 입력: ");
scanf("%d", &readData);
if(readData < 1)
break;
arr[readCount++] = readData;
}
for(i=0; i<readCount; i++)
printf("%d ", arr[i]);
return 0;
}이는 1 미만의 값이 입력될 때까지 입력이 계속되는 간단한 예제이니 별도의 설명은 필요 없을 것이다.
그런데 이 예제에서는 다음과 같은 배열의 단점을 분명히 보여주고 있다.
"배열은 메모리의 특성이 정적이어서(길이의 변경이 불가능해서) 메모리의 길이를 변경하는 것이 불가능합니다."위 예제를 실행한 후 1 미만의 값을 입력하지 않고 계속해서 자연수만 입력을 하면 할당된 배열의 길이를 넘어서는 문제가 발생한다.
이렇듯 특성이 정적인 배열은 필요로 하는 메모리의 크기에 유연하게 대처하지 못한다.
그래서 등장한 것이 '동적인 메모리의 구성'이다.
그럼 이것이 무엇인지 다음 예제를 통해서 보이겠다.
LinkedRead.c
#include <stdio.h>
#include <stdlib.h>
typedef struct _node
{
int data;
struct _node * next;
} Node;
int main(void)
{
Node * head = NULL; // NULL 포인터 초기화
Node * tail = NULL;
Node * cur = NULL;
Node * newNode = NULL;
int readData;
/**** 데이터를 입력 받는 과정 ****/
while(1)
{
printf("자연수 입력: ");
scanf("%d", &readData);
if(readData < 1)
break;
/*** 노드의 추가과정 ***/
newNode = (Node*)malloc(sizeof(Node));
newNode->data = readData;
newNode->next = NULL;
if(head == NULL)
head = newNode;
else
tail->next = newNode;
tail = newNode;
}
printf("\n");
/**** 입력 받은 데이터의 출력과정 ****/
printf("입력 받은 데이터의 전체출력! \n");
if(head == NULL)
{
printf("저장된 자연수가 존재하지 않습니다. \n");
}
else
{
cur = head;
printf("%d ", cur->data); // 첫 번째 데이터 출력
while(cur->next != NULL) // 두 번째 이후의 데이터 출력
{
cur = cur->next;
printf("%d ", cur->data);
}
}
printf("\n\n");
/**** 메모리의 해제과정 ****/
if(head == NULL)
{
return 0; // 해제할 노드가 존재하지 않는다.
}
else
{
Node * delNode = head;
Node * delNextNode = head->next;
printf("%d을(를) 삭제합니다. \n", head->data);
free(delNode); // 첫 번째 노드의 삭제
while(delNextNode != NULL) // 두 번째 이후의 노드 삭제 위한 반복문
{
delNode = delNextNode;
delNextNode = delNextNode->next;
printf("%d을(를) 삭제합니다. \n", delNode->data);
free(delNode);
}
}
return 0;
}먼저 정의된 구조체를 보자.
typedef struct _node
{
int data;
struct _node * next;
} Node;위 구조체의 멤버 next는 Node(_node)형 구조체 변수의 주소 값을 저장할 수 있는 포인터 변수이다!
이 멤버로 인해서 모든 Node형 구조체 변수는 다른 Node형 구조체 변수를 가리킬 수 있으므로, Node형 구조체 변수들을 연결하는 것이 가능하다.
따라서 Node형 구조체를 대상으로 다음과 같은 일이 가능하다 할 수 있다.
"필요할 때마다 공간을 하나씩 마련해서 그곳에 데이터를 저장하고 이들을 배열처럼 서로 연결한다."그런데 프로그램 실행 중에 필요할 때마다 메모리 공간을 마련하는 유일한 방법은 'malloc 또는 그와 유사한 성격의 함수를 호출하는 메모리의 동적 할당'이므로 위의 글은 다음과 같이 구체적으로 정리할 수 있다.
"필요할 때마다 구조체 변수를 하나씩 동적 할당해서 이들을 연결한다."이것이 '연결 리스트'의 기본 원리이다.
그리고 앞서 정의한 구조체 Node의 변수를 가리켜 '노드'라 한다.
이어서 세세히 코드를 분석할 차례인데, 구조체 Node의 변수를 그림상에서 다음과 같이 표현할 수 있다.

위 그림에서 보이듯이 '데이터를 저장할 장소'와 '다른 변수를 가리키기 위한 장소'가 구분되어 있다.
그래서 둘 이상의 Node가 연결된 상황은 다음과 같이 표현하고자 한다.

NULL은 의미 있는 주소 값이 아니지만, 위 그림에서 NULL도 별도의 블록으로 표현하였다.
그럼 이어서 본격적으로 코드 분석에 들어가기로 하겠다.
예제 LinkedRead.c를 두고서 '연결 리스트를 구현한 겁니다.'라고 말할 수 있을까?
이는 제대로 된 연결 리스트의 구현결과를 보이기 이전에, 쉬운 이해를 위한 예제에 지나지 않는다.
하지만 이것도 연결 리스트의 구현결과이다.
따라서 이 코드를 잘 이해하면 상대적으로 연결 리스트를 쉽게 공부할 수 있다.
그럼 예제의 main 함수에 처음 등장하는 다음 포인터 변수의 선언을 보자.
Node * head = NULL; // 리스트의 머리를 가리키는 포인터 변수
Node * tail = NULL; // 리스트의 꼬리를 가리키는 포인터 변수
Node * cur = NULL; // 저장된 데이터의 조회에 사용되는 포인터 변수이들은 연결 리스트에서 주요한 역할을 하는 포인터 변수들이다.
따라서 이들이 어떻게 사용되는지 이해하는 것이 연결 리스트 전체의 이해에 도움이 된다.
그럼 위의 포인터 변수들이 선언된 상황을 그림으로 표현해보겠다.
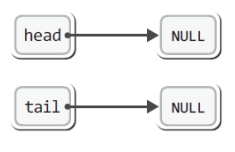
위 그림에서는 프로그램이 처음 시작되었을 때 구조체 Node의 포인터 변수 head와 tail이 NULL을 가리키고 있는 상황을 보이고 있다.
이 상황에서 다음 반복문을 처음 실행하게 된다.
while(1)
{
printf("자연수 입력: ");
scanf("%d", &readData);
if(readData < 1)
break;
/*** 노드의 추가과정 ***/
newNode = (Node*)malloc(sizeof(Node)); // 노드의 생성
newNode->data = readData; // 노드에 데이터 저장
newNode->next = NULL; // 노드의 next를 NULL로 초기화
if(head == NULL) // 첫 번째 노드라면
head = newNode; // 첫 번째 노드를 head가 가리키게 함
else // 두 번째 이후 노드라면
tail->next = newNode;
tail = newNode; // 노드의 끝을 tail이 가리키게 함
}위의 반복문에서 첫 번째 노드가 추가되는 상황을, 다시 말해서 반복문이 처음 실행되는 상황을 살펴보자.
먼저 다음 세 문장에 의해서 노드가 생성되고 또 초기화된다.
newNode = (Node*)malloc(sizeof(Node)); // 노드의 생성
newNode->data = readData; // 노드에 데이터 저장
newNode->next = NULL; // 노드의 next를 NULL로 초기화위의 코드에서 readData에 저장된 값을 2로 가정할 때, 위의 세 문장을 실행한 결과는 다음과 같다.
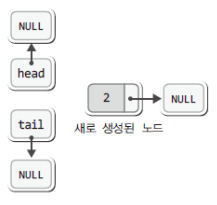
위의 상태에서 포인터 변수 head가 가리키는 것이 NULL이니, 이어서 다음 구문을 실행하게 된다.
if(head == NULL) // 첫 번째 노드라면
head = newNode; // 첫 번째 노드를 head가 가리키게 함따라서 다음 그림과 같이 head가 새로운 노드를 가리키는 상태가 된다.
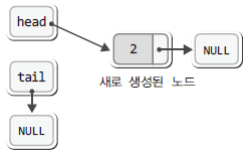
그리고 이어서 while문의 마지막에 위치한 다음 문장을 실행하게 된다.
tail = newNode; // 노드의 끝을 tail이 가리키게 함그리고 그 결과는 다음과 같다.
이것이 첫 번째 노드의 추가가 완료된 상태이다.
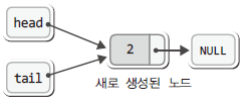
노드의 추가를 표현하기 용이하도록 위의 그림을 다음과 같이 같이 다시 그려보았다.
참고로 아래 그림에서는 NULL을 사선으로 표현하였다.
즉 사선은 NULL이 저장되었음을 의미한다.
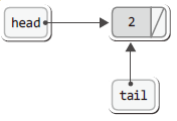
위 그림에서 주목할 사실은 head와 tail이 첫 번째 노드를 가리키고 있다는 점이다.
이미 짐작했겠지만 head는 리스트의 머리를 가리키고 tail은 리스트의 꼬리를 가리킨다.
노드가 몇 개가 추가되건 이는 변함이 없어야 한다.
그럼 이어서 두 번째 노드를 추가하는 과정을 추적해보자.
두 번째 노드는 연결 리스트의 끝, 다시 말해서 tail이 가리키는 노드의 뒤에 연결되어야 하기 때문에 새 노드의 생성 및 초기화 이후에는 else 구문에 담긴 다음 문장을 실행하게 된다.
else // 두 번째 이후 노드라면
tail->next = newNode;
tail = newNode;따라서 노드의 끝을 tail이 가리키게 하고 반복문의 마지막 문장까지 실행할 경우, 그리고 새 노드에 저장된 값을 4로 가정할 경우 그 결과는 다음과 같다.
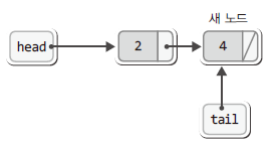
정리하면, 연결 리스트에서 head는 첫 번째 노드를, 그리고 tail은 마지막 노드를 가리킨다.
그리고 추가되는 노드들은 꼬리에 꼬리를 물어서 저장되기 때문에 2, 4, 6, 8이 순서대로 저장이 되면 다음의 모습을 띠게 된다.
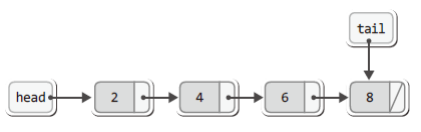
이렇게 해서 연결 리스트의 '데이터 저장'에 대한 기본 개념을 모두 설명하였다.
참고로 지금껏 그림을 그려가면서 설명했듯이 여러분도 그림을 그리면서 이해해야 한다.
누구나 자료구조는, 특히 연결 리스트는 그림을 그려가면서 공부해야 한다.
솔직히 말하자면 자료구조는 코드를 통해서 공부하는 과목이 아니다.
코드를 통한 학습 이전에, 그림으로 설명하고 그림으로 이해해야 하는 과목이다.
이번엔 조회와 관련된 코드를 살펴볼 텐데 '삽입'과 비교할 수 없이 쉬운 것이 '조회'이다.
그럼 조회 관련 코드를 보자.
if(head == NULL)
{
printf("저장된 자연수가 존재하지 않습니다. \n");
}
else
{
cur = head; // cur이 리스트의 첫 번째 노드를 가리킨다
printf("%d ", cur->data); // 첫 번째 데이터 출력
while(cur->next != NULL) // 연결된 노드가 존재하면
{
cur = cur->next; // cur이 다음 노드를 가리키게 한다.
printf("%d ", cur->data); // cur이 가리키는 노드를 출력한다.
}
}위의 코드에서 else 구문에 속해있는 다음 문장이 실행되면,
cur = head;그리고 연결 리스트에 2, 4, 6, 8이 이미 저장된 상태라고 가정하면, cur은 2가 저장된 연결 리스트의 첫 번째 노드를 가리키게 된다.
따라서 cur을 이용한 첫 번째 데이터의 출력이 가능하다.
그리고 이어서 다음 반복문을 실행하게 되는데,
while(cur->next != NULL) // 연결된 노드가 존재하면
{
cur = cur->next; // cur이 다음 노드를 가리키게 한다.
printf("%d ", cur->data); // cur이 가리키는 노드를 출력한다.
}위 반복문의 핵심은 다음 문장에 있다.
cur = cur->next;위의 문장으로 인해서 cur은 다음과 같이 모든 노드를 가리키며 이동하게 된다.
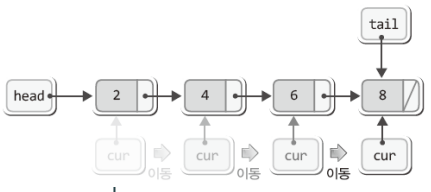
이렇듯 main 함수의 앞부분에서 선언된 포인터 변수 cur은 리스트 안을 돌아다닐 때 사용이 된다.
예제 LinkedRead.c의 데이터 삭제과정은 처음 보면 혼란스럽다.
하지만 그림을 그려가면서 이해하면 혼란을 줄일 수 있다.
예제에서 보인 삭제관련 코드는 다음과 같다.
if(head == NULL)
{
return 0; // 삭제할 노드가 존재하지 않는다.
}
else
{
Node * delNode = head;
Node * delNextNode = head->next;
printf("%d을(를) 삭제합니다. \n", head->data);
free(delNode); // 첫 번째 노드 삭제
while(delNextNode != NULL) // 두 번째 이후 노드 삭제
{
delNode = delNextNode;
delNextNode = delNextNode->next;
printf("%d을(를) 삭제합니다. \n", delNode->data);
free(delNode); // 두 번째 이후의 노드 삭제
}
}그럼 삭제의 과정에서 제일 먼저 등장하는 다음 두 문장을 보자.
Node * delNode = head;
Node * delNextNode = head->next;head가 가리키는 노드의 삭제를 위해서 두 개의 포인터 변수를 추가로 선언한 사실에 주목하자.
그리고 아래의 그림에서 이 둘이 가리키는 대상에도 주목을 하자.
아래의 그림에서는 편의상 delNode는 dN으로, delNextNode는 dNN으로 표시하였다.
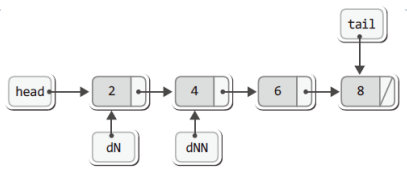
위 그림에서와 같이 dNN이라는 이름의 포인터 변수를 둬서 '삭제될 노드'가 가리키는 다음 노드의 주소 값을 저장하는 이유는 다음과 같다.
"head가 가리키는 노드를 그냥 삭제해 버리면 그 다음 노드에 접근이 불가능합니다."즉 '삭제될 노드가 가리키는 다음 노드의 주소 값'을 별도로 저장해 두지 않으면 다음과 같은 상황이 연출된다.
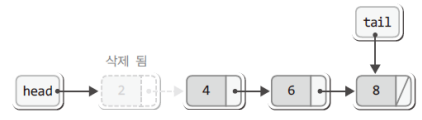
위 그림에서 보이듯이 4가 저장된 노드의 주소 값을 아는 것은 2가 저장된 노드가 유일한데, 이 노드를 그냥 소멸시킨 결과로 4가 저장된 노드의 주소 값은 어디에도 존재하지 않게 된다.
즉 4가 저장된 노드는 이제 어떠한 방법을 통해서도 접근이 불가능하다.
그래서 삭제될 노드가 가리키는 다음 노드의 주소 값을 별도로 저장하는 것이다.
그럼 다시 본론으로 돌아와서 포인터 변수 dNN 선언 이후에 이어서 진행되는 다음 문장의 실행결과를 생각해보자.
free(delNode);이로써 첫 번째 노드가 소멸되어 다음의 상태가 된다.
"참고로 head가 가리키는 노드가 소멸되었으니 head가 다음 노드를 가리키도록 하는 것이 연결 리스트의 원칙이지만,
본 삭제과정의 목적은 연결 리스트 전체의 소멸에 있으므로 굳이 head가 다음 노드를 가리키도록 하지 않았다."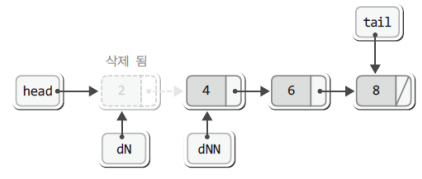
이제 위의 상태에서, 다시 말해 free 함수호출 이후에 다음의 반복문을 실행하게 된다.
while(delNextNode != NULL) // 두 번째 이후 노드 삭제
{
delNode = delNextNode;
delNextNode = delNextNode->next;
printf("%d을(를) 삭제합니다. \n", delNode->data);
free(delNode); // 두 번째 이후의 노드 삭제
}포인터 변수 delNextNode를 참조하여 추가로 삭제할 노드가 있는지 확인한 다음, 반복문 내에서 다음 두 문장을 실행한다.
delNode = delNextNode;
delNextNode = delNextNode->next;그리고 그 결과로 두 포인터 변수 delNode(dN)과 delNextNode(dNN)이 가리키는 대상은 한 칸씩 오른쪽으로 이동을 한다.
이어서 반복문의 끝에서 free 함수의 호출을 통해 delNode가 가리키는 대상을 소멸하여 다음의 상태가 되게 한다.
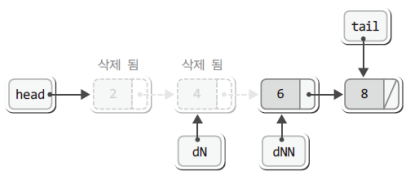
여기까지가 반복문의 한 사이클이다.
즉 반복문 내에서 하는 일은 delNode와 delNextNode를 한 칸씩 이동시키면서 delNode가 가리키는 대상을 소멸하는 것이 전부이다.
그리고 이 과정을 마지막 노드가 소멸할 때까지 계속 진행하니 결과적으로 모든 노드가 소멸되는 것이다.
2. 단순 연결 리스트의 ADT 구현
기능적으로 무엇인가를 변경하거나 추가하지 않는다면 ADT를 변경할 이유는 없다.
그래서 앞서 정의한 리스트 ADT를 그대로 적용해도 된다.


위의 ADT에 새로 추가된 함수는 SetSortRule이 전부이고, 그 이외에는 앞서 정의한 리스트의 ADT와 완전히 동일하다.
그리고 위의 ADT에는 명시되어 있지는 않지만 우리는 다음 내용과 관련해서 결정을 해야 한다.
"새 노드를 추가할 때, 리스트의 머리와 꼬리 중 어디에 저장을 할 것인가?"두 가지 방법 모두 장점과 단점이 있다.
우선 머리에 추가할 경우의 장점과 단점은 다음과 같다.
- 장점: 포인터 변수 tail이 불필요하다.
- 단점: 저장된 순서를 유지하지 않는다.반면 꼬리에 추가할 경우의 장점과 단점은 다음과 같다.
- 장점: 저장된 순서가 유지된다.
- 단점: 포인터 변수 tail이 필요하다.어떠한 방법이 더 좋다고 판단할 성격의 문제는 아니다.
하지만 학습과정에서는, 그리고 구현까지 해야한다면 머리에 추가하는 방법을 선호하는데 그 이유는 다음과 같다.
"포인터 변수 tail을 유지하기 위해서 넣어야 할 부가적인 코드가 번거롭게 느껴질 수 있다."
"게다가 리스트 자료구조는 저장된 순서를 유지해야 하는 자료구조가 아니다."비교적 많은 수의 자료구조 서적들도 노드를 머리에 추가하는 방식으로 연결 리스트를 구현한다.
자! 그럼 새로 추가된 함수 SetSortRule에 대해서 이야기해 보자.
그에 앞서 C언어의 '함수 포인터'를 잘 알고 있어야 한다.
만약에 함수 포인터를 잘 알고 있다면, 다음 함수의 매개변수 선언이 의미하는 바를 모르지 않을 것이다.
void SetSortRule(List * plist, int (*comp)(LData d1, LData d2));이 함수는 연결 리스트의 정렬기준을 지정하기 위한 함수이다.
위 함수의 두 번째 매개변수 선언을 보자.
int (*comp)(LData d1, LData d2)함수 포인터를 잘 알고 있다면, SetSortRule 함수의 매개변수 선언에 있어서 이것이 의미하는 바가 다음과 같음을 알 수 있을 것이다.
"반환형이 int이고 LData형 인자를 두 개 전달받는 함수의 주소 값을 두 번째 인자로 전달하라"따라서 다음과 같이 정의된 함수의 주소 값이 SetSortRule 함수의 두 번째 인자가 될 수 있다.
int WhoeIsPrecede(LData d1, LData d2)
{
if(d1 < d2)
return 0;
else
return 1;
}그리고 SetSortRule의 두 번째 인자로 전달되는 함수는 위의 함수 정의에서 보이듯이 다음 조건을 갖춰서 정의해야 하는 것으로 결정하겠다!
"매개변수 d1에 전달되는 인자가 정렬 순서상 앞서서 head에 더 가까워야 하는 경우에는 0을 반환하고,
매개변수인 d2에 전달되는 인자가 정렬 순서상 앞서거나 같은 경우에는 1을 반환한다."이렇듯 반환 값이 어떻게 되고 또 그것이 어떤 의미를 갖는지는, 연결 리스트를 구현하는 우리들이 결정할 문제이다!
따라서 이는 얼마든지 바꿀 수 있다.
여기서는 반환 값을 0과 1로 제한했지만, 더 다양한 반환 값과 의미를 부여해도 된다.
그럼 예를 들어서 D1과 D2라는 데이터가 있다고 가정해보자.
그리고 이를 대상으로 다음과 같이 함수를 호출한다고 가정해보자.
int cr = WhoIsPrecede(D1, D2);그 결과 cr에 반환된 값이 0이라면 D1이 정렬 순서상 앞선다는 의미이므로, D1과 D2는 다음의 순서로 저장되어야 한다.

반대로 cr에 반환된 값이 1이라면 D1이 정렬 순서상 앞선다는 의미이므로, D1과 D2는 다음의 순서로 저장되어야 한다.

우선은 이 정도만 설명하겠다.
SetSortRule 함수가 어떻게 활용되고, 또 연결 리스트 내부적으로 어떠한 의미를 지니는지는 천천히 설명하기로 하겠다.
앞서 예제 LinkedRead.c에서 구현한 연결 리스트는 다음의 구조를 지녔다.
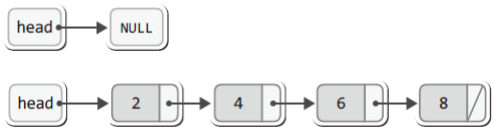
위 그림에서 보이듯이 첫 번째 노드는 포인터 변수 head가 가리킨다는 점에서 다른 노드들과 차이가 있다.
때문에, 이미 느꼈는지 모르겠지만 다음과 같은 단점이 있었다.
"노드를 추가, 삭제 그리고 조회하는 방법에 있어서 첫 번째 노드와 두 번째 이후의 노드에 차이가 있습니다."특히 이후에 구현할 연결 리스트에서는 그 차이가 더 커지기 때문에 이는 분명 단점이라 할 수 있다.
그래서 다음의 구조로 연결 리스트를 구현하고자 한다.

우선 포인터 변수 tail이 사라졌다.
노드를 앞에서부터 채우기로 하였으니 이는 불필요하다.
그리고 리스트의 맨 앞에 '더미 노드(dummy node)'라는 것을 넣어 두었다.
이는 유효한 데이터를 지니지 않는 그냥 빈 노드를 일컫는 말이다.
하지만 이렇듯 빈 노드를 미리 넣어 두면, 처음 추가되는 노드가 구조상 두 번째 노드가 되므로 노드의 추가, 삭제 및 조회의 과정을 일관된 형태로 구성할 수 있다.
다음은 노드를 표현한 구조체의 정의이다.
그리고 이는 연결 리스트의 구현에서 결코 빠지지 않는다.
typedef struct _node
{
int data;
struct _node * next;
} Node;그런데 연결 리스트의 구현에 필요한 다음 유형의 변수들은 별도의 구조체로 묶지 않고 그냥 main 함수의 지역변수로 선언하기도 하고, 더 나쁜 경우에는 전역변수로 선언하기도 한다.
Node * head = NULL;
Node * tail = NULL;
Node * cur = NULL;단순히 연결 리스트가 어떠한 흐름을 갖는지 코드 수준에서만 공부한다면 괜찮을지 모르겠지만, 그것이 전부가 아니라면 위 유형의 포인터 변수들은 main 함수 내에서도, 전역변수로도 선언해서는 절대 안 된다.
리스트 자료구조가 하나만 사용되는 법이 없기 때문이다.
필요에 따라서 여러 개의 리스트가 필요한데 이런 상황에서 head와 cur과 같은 포인터 변수를 전역변수로 선언해야 한다면, 끔찍하지 않을 수 없다.
물론 이것이 이유의 전부는 아니다.
리스트를 하나만 필요로 한다 하더라도 이러한 구현방식은 프로그램의 구조를 좋지 못한 형태로 이끄는 원인이 된다.
따라서 head와 cur과 같은 포인터 변수를 묶어서 다음과 같이 연결 리스트를 의미하는 구조체를 별도로 정의해야 한다.
typedef struct _linkedList
{
Node * head;
Node * cur;
Node * before;
int numOfData;
int (*comp)(LData d1, LData d2);
} LinkedList;이는 앞 챕터에서 정의한 구조체 ArrayList와 그 성격이 동일하다.
그리고 구조체의 멤버 중에서 before와 comp의 용도가 궁금할 텐데, 이는 연결 리스트의 구현을 보이면서 소개하기로 하겠다.
그럼 이제 우리가 구현할 연결 리스트를 위한 헤더파일을 소개하겠다.
DLinkedList.h
#ifndef __D_LINKED_LIST_H__
#define __D_LINKED_LIST_H__
#define TRUE 1
#define FALSE 0
typedef int LData;
typedef struct _node
{
LData data;
struct _node * next;
} Node;
typedef struct _linkedList
{
Node * head;
Node * cur;
Node * before;
int numOfData;
int (*comp)(LData d1, LData d2);
} LinkedList;
typedef LinkedList List;
void ListInit(List * plist);
void LInsert(List * plist, LData data);
int LFirst(List * plist, LData * pdata);
int LNext(List * plist, LData * pdata);
LData LRemove(List * plist);
int LCount(List * plist);
void SetSortRule(List * plist, int (*comp)(LData d1, LData d2));
#endif위의 헤더파일에 선언된 함수는 배열 기반 리스트의 헤더파일에 선언된 함수와 동일하다.
다만 정렬기준의 지정을 목적으로 SetSortRule 함수의 선언이 추가되었을 뿐이다.
참고로 이 함수에 대해서는 연결 리스트를 구현한 다음에 별도로 언급하겠다.
다음은 연결 리스트를 표현한 구조체의 정의이다.
연결 리스트를 생성하기 원한다면 다음 구조체의 변수를 하나 선언하거나 동적으로 할당하면 된다.
따라서 이후로는 다음 구조체의 변수를 가리켜 그냥 '리스트'라 하겠다.
typedef struct _linkedList
{
Node * head;
Node * cur;
Node * before;
int numOfData;
int (*comp)(LData d1, LData d2);
} LinkedList;위 구조체 변수가 선언되면 이를 대상으로 초기화를 진행해야 하는데, 이때 호출되는 함수는 다음과 같다.
void ListInit(List * plist)
{
plist->head = (Node*)malloc(sizeof(Node)); // 더미 노드의 생성
plist->head->next = NULL;
plist->comp = NULL;
plist->numOfData = 0;
}그리고 위의 초기화 결과를 그림으로 정리하면 다음과 같다.
이 그림에서 중요한 사실은 더미 노드가 존재한다는 점이다.
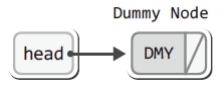
위 그림에 표현되지 않았지만 리스트의 멤버 comp가 NULL로, 멤버 numOfData가 0으로 초기화된다는 사실을 더불어 기억하자.
이제 위의 상황에서 노드의 추가를 위해 호출되는 함수는 다음과 같다.
void LInsert(List * plist, LData data)
{
if(plist->comp == NULL)
FInsert(plist, data);
else
SInsert(plist, data);
}위의 함수에서 보이듯이 노드의 추가는 리스트의 멤버 comp에 무엇이 저장되어 있느냐에 따라서 FInsert 또는 SInsert 함수를 통해서 진행이 된다.
그런데 이 두 함수 모두 헤더파일에 선언된 함수가 아니다.
즉 리스트를 사용하는 프로그래머는 이 두 함수를 직접 호출할 수 없다.
리스트 내부적으로 호출이 되도록 정의된 함수들이기 때문이다.
그럼 먼저 comp가 NULL일 때 호출되는 FInsert 함수를 보자.
void FInsert(List * plist, LData data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = plist->head->next;
plist->head->next = newNode;
(plist->numOfData)++;
}위의 함수를 이해하기 위해서는 현재 포인터 변수 head가 NULL이 아닌, 더미 노드를 가리키고 있다는 사실을 잊지 말아야 한다.
그리고 위의 함수에는 if...else 구문이 없다는 사실에도 주목할 필요가 있다.
이는 모든 노드의 추가과정이 일관되게 정의되었음을 뜻하는 것이며, 이것이 바로 더미 노드가 주는 이점이기 때문이다.
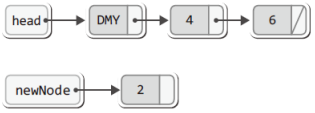
그럼 현재 연결 리스트에 4와 6이 저장된 상태에서 위의 함수가 다음과 같이 호출되었다고 가정해보자.
FInsert(plist, 2);그러면 이어서 다음 두 문장이 차례로 실행된다.
Node * newNode = (Node*)malloc(sizeof(Node)); // 새 노드 생성
newNode->data = data; // 새 노드에 데이터 저장그리고 그 결과를 그림으로 표현하면 다음과 같다.
이어서 다음 두 문장이 실행된다.
newNode->next = plist->head->next;
plist->head->next = newNode;그리고 그 결과를 그림으로 표현하면 다음과 같다.
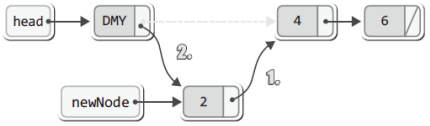
이렇게 해서 comp가 NULL일 때 노드의 추가과정을 모두 보였다.
이어서 리스트의 멤버 comp가 NULL이 아닐 때 호출되는 SInsert 함수에 대해서 설명할 차례인데, 이는 잠시 뒤로 미루고 조회와 삭제에 대해서 먼저 설명하겠다.
우리가 정의한 리스트 ADT를 기준으로 '조회'하면 떠오르는 두 함수는 LFirst와 LNext이다.
이 두 함수의 기능은 배열 리스트의 LFirst 그리고 LNext와 동일하니, 기능 및 사용법에 관한 설명을 추가하지는 않겟다.
그럼 먼저 LFirst 함수를 볼 텐데 아래의 주석에서 말하는 '첫 번째 노드'는 더미 노드의 다음에 연결된 노드를 뜻하는 것임에 유의하자.
그리고 이후에도 더미 노드의 다음에 연결된 노드를 가리켜 '첫 번째 노드'라 하겠다.
int LFirst(List * plist, LData * pdata)
{
if(plist->head->next == NULL) // 더미 노드가 NULL을 가리킨다면
return FALSE; // 반환할 데이터가 없다
plist->before = plist->head; // before는 더미 노드를 가리키게 함
plist->cur = plist->head->next; // cur은 첫 번째 노드를 가리키게 함
*pdata = plist->cur->data; // 첫 번째 노드의 데이터를 전달
return TRUE; // 데이터 반환 성공
}위 함수의 핵심이 되는 두 문장은 다음과 같다.
plist->before = plist->head; // before는 더미 노드를 가리키게 함
plist->cur = plist->head->next; // cur은 첫 번째 노드를 가리키게 함그리고 리스트에 2, 4, 6, 8이 저장된 상황에서 LFirst 함수가 호출되고, 이어서 위의 두 문장이 실행되었을 때의 상황을 그림으로 정리하면 다음과 같다.
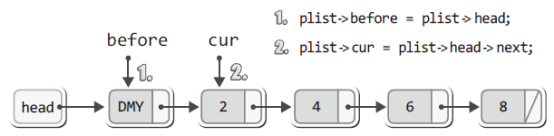
때문에 이어서 실행되는 다음 문장을 통해서 첫 번째 데이터가 전달된다(반환된다).
*pdata = plist->cur->data; // 첫 번째 노드의 데이터를 전달그렇다면 리스트 구조체의 멤버에 before를 둬서 멤버 cur보다 하나 앞선 노드를 가리키게 하는 이유는 무엇일까?
이는 잠시 후에 설명하는 '노드의 삭제'와 관련이 있으니 일단은 before가 cur보다 하나 앞선 노드를 가리킨다는 사실에 주목하자.
그리고 이 관계는 이어서 소개하는 LNext함수가 호출되어도 유지되어야 한다.
int LNext(List * plist, LData * pdata)
{
if(plist->cur->next == NULL) // cur이 NULL을 가리킨다면
return FALSE; // 반환할 데이터가 없다
plist->before = plist->cur; // cur이 가리키던 것을 before가 가리킴
plist->cur = plist->cur->next; // cur은 그 다음 노드를 가리킴
*pdata = plist->cur->data; // cur이 가리키는 노드의 데이터 전달
return TRUE; // 데이터 반환 성공
}이렇듯 LNext 함수는 LFirst 함수와 많이 유사하다.
그리고 LFirst 함수와 유사하게 다음 두 문장을 LNext 함수의 핵심이라 할 수 있다.
plist->before = plist->cur;
plist->cur = plist->cur->next;그리고 다음 그림에서 보이듯이 위의 두 문장을 실행한 결과로 cur과 before는 가리키는 대상을 하나씩 오른쪽으로 이동하게 된다.
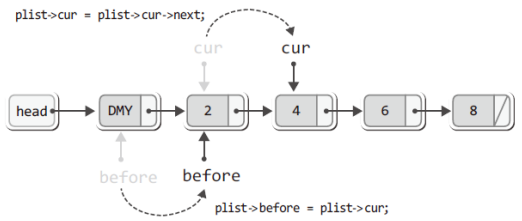
이렇듯 cur이 마지막 노드를 가리킬 때까지 LNext 함수가 호출되면, cur과 before가 한 칸씩 다음 노드로 이동을 하니 cur을 이용해서 모든 데이터를 참조하게 된다.
연결 리스트에서 데이터의 추가만큼이나 신경 써야 할 것이 삭제이다.
그리고 삭제를 담당하는 LRemove 함수를 구현하기에 앞서 그림으로 삭제의 과정을 파악해야 한다.
이전에 구현한 배열 기반 리스트에서와 마찬가지로 LRemove 함수의 기능은 다음과 같다.
"바로 이전에 호출된 LFirst 혹은 LNext 함수가 반환한 데이터를 삭제한다."그럼 다음의 상황에서 LRemove 함수가 호출되었다고 가정해보자.
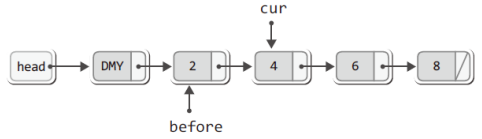
상황이 위와 같다는 것은 LNext 함수의 호출을 통해서 4가 반환되었다는 뜻이다.
따라서 LRemove 함수의 호출 시 소멸시켜야 하는 노드는 현재 cur이 가리키는, 4가 저장된 노드이다.
따라서 삭제의 최종 결과는 다음과 같다.
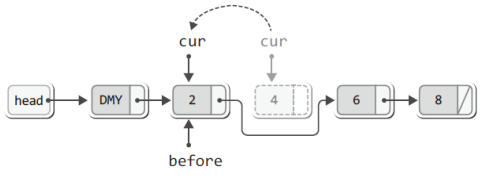
위의 그림에서 주목할 것은 cur의 위치가 재조정되었다는 사실이다.
4가 저장된 노드가 지워졌다고 해서 6이 저장된 노드를 가리키게 해서는 안 된다.
그렇게 되면 6까지 참조가 이뤄졌다는 뜻이 되기 때문이다.
따라서 cur이 가리키는 위치를 한 칸 왼쪽으로 이동시켜야 한다.
그리고 이렇듯 cur의 위치를 한 칸 왼쪽으로 이동시키기 위해서는 before의 도움이 필요하다.
"cur만 한 칸 왼쪽으로 이동시키면, before와 cur이 동일한 위치를 가리키게 되니까 before도 한 칸 왼쪽으로 이동시켜야 하는 것 아닌가요?"재차 LFirst 또는 LNext 함수가 호출되면 before는 다시 cur보다 하나 앞선 노드를 가리키게 되므로, 굳이 이 상황에서 before의 위치까지 재조정할 필요는 없다.
무엇보다도 노드들이 한쪽 방향으로만 연결되어 있기 때문에 before를 한 칸 왼쪽으로 이동시키기 위해서는 그만큼 코드를 다시 짜야하고 그 과정이 복잡하다.
자! 그럼 LRemove 함수를 보이겠다.
LData LRemove(List * plist)
{
Node * rpos = plist->cur; // 소멸 대상의 주소 값을 rpos에 저장
LData rdata = rpos->data; // 소멸 대상의 데이터를 rdata에 저장
plist->before->next = plist->cur->next; // 소멸 대상을 리스트에서 제거
plist->cur = plist->before; // cur이 가리키는 위치를 재조정
free(rpos); // 리스트에서 제거된 노드 소멸
(plist->numOfData)--; // 저장된 데이터의 수 하나 감소
return rdata; // 제거된 노드의 데이터 반환
}위 함수가 실행되고 이어서 다음 두 문장이 실행되었다고 가정해보자.
Node * rpos = plist->cur; // 소멸 대상의 주소 값을 rops에 저장
LData rdata = rpos->data; // 소멸 대상의 데이터를 rdata에 저장그러면 rpos는 cur과 같은 곳을 가리키게 되어 다음의 상황에 놓이게 된다.
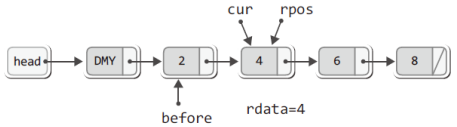
이로써 삭제를 위한 기본적인 준비는 갖춰진 셈이다.
따라서 다음 두 문장을 이어서 실행하게 된다.
plist->before->next = plist->cur->next; // 소멸 대상을 리스트에서 제거
plist->cur = plist->before; // cur이 가리키는 위치를 재조정그리고 그 결과는 다음과 같다.
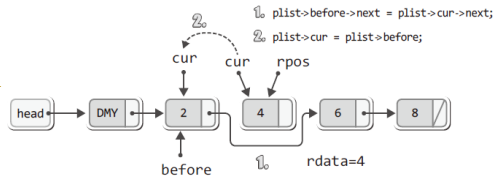
위의 단계까지만 진행되어도 일단 리스트에서 노드는 제거된 셈이다.
따라서 마지막으로 할 일은 제거된 노드를 완전히 소멸시키면서 데이터의 수를 하나 감소시키고, 이어서 제거된 노드에 저장된 값을 반환하는 일인데, 이는 다음 세 문장에 의해서 실행이 된다.
free(rpos); // 리스트에서 제거된 노드 소멸
(plist->numOfData)--; // 저장된 데이터의 수 하나 감소
return rdata; // 제거된 노드의 데이터 반환이로써 노드의 제거는 완전히 끝이 났다.
그리고 그 결과는 다음과 같이 정리할 수 있다.
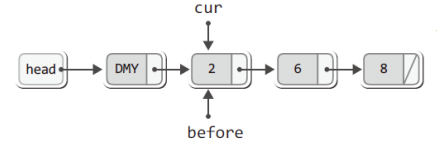
지금가지 삭제의 과정을 그림과 함께 설명하였는데, 여러분도 이 과정을 그림으로 우선 설명할 수 있어야 한다.
그림으로 설명이 가능해야 코드로도 구현이 가능하기 때문이다.
모든 것을 설명한 듯 보이나 아직 정렬 삽입에 관한 부분을 설명하지 않았다.
하지만 지금까지 우리가 이해한 내용만 가지고도 예제를 작성해서 그 결과를 확인할 수 있다.
그럼 지금까지 구현한 연결 리스트의 결과를 담고 있는 헤더파일과 소스파일을 아래에 보이겠다.
비록 헤더파일은 앞서 제시하였지만, 정리차원에서 다시 한번 보이겠다.
DLinkedList.h
#ifndef __D_LINKED_LIST_H__
#define __D_LINKED_LIST_H__
#define TRUE 1
#define FALSE 0
typedef int LData;
typedef struct _node
{
LData data;
struct _node * next;
} Node;
typedef struct _linkedList
{
Node * head;
Node * cur;
Node * before;
int numOfData;
int (*comp)(LData d1, LData d2);
} LinkedList;
typedef LinkedList List;
void ListInit(List * plist);
void LInsert(List * plist, LData data);
int LFirst(List * plist, LData * pdata);
int LNext(List * plist, LData * pdata);
LData LRemove(List * plist);
int LCount(List * plist);
void SetSortRule(List * plist, int (*comp)(LData d1, LData d2));
#endifDLinkedList.c
#include <stdio.h>
#include <stdlib.h>
#include "DLinkedList.h"
void ListInit(List * plist)
{
plist->head = (Node*)malloc(sizeof(Node));
plist->head->next = NULL;
plist->comp = NULL;
plist->numOfData = 0;
}
void FInsert(List * plist, LData data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = plist->head->next;
plist->head->next = newNode;
(plist->numOfData)++;
}
void SInsert(List * plist, LData data)
{
Node * newNode = (Node*)malloc(sizeof(Node));
Node * pred = plist->head;
newNode->data = data;
while(pred->next != NULL &&
plist->comp(data, pred->next->data) != 0)
{
pred = pred->next;
}
newNode->next = pred->next;
pred->next = newNode;
(plist->numOfData)++;
}
void LInsert(List * plist, LData data)
{
if(plist->comp == NULL)
FInsert(plist, data);
else
SInsert(plist, data);
}
int LFirst(List * plist, LData * pdata)
{
if(plist->head->next == NULL)
return FALSE;
plist->before = plist->head;
plist->cur = plist->head->next;
*pdata = plist->cur->data;
return TRUE;
}
int LNext(List * plist, LData * pdata)
{
if(plist->cur->next == NULL)
return FALSE;
plist->before = plist->cur;
plist->cur = plist->cur->next;
*pdata = plist->cur->data;
return TRUE;
}
LData LRemove(List * plist)
{
Node * rpos = plist->cur;
LData rdata = rpos->data;
plist->before->next = plist->cur->next;
plist->cur = plist->before;
free(rpos);
(plist->numOfData)--;
return rdata;
}
int LCount(List * plist)
{
return plist->numOfData;
}
void SetSortRule(List * plist, int (*comp)(LData d1, LData d2))
{
plist->comp = comp;
}다음은 위의 연결리스트를 기반으로 작성된 main 함수와 그 실행결과이다.
DLinkedListMain.c
#include <stdio.h>
#include "DLinkedList.h"
int main(void)
{
// List의 생성 및 초기화 /////////////////////////////
List list;
int data;
ListInit(&list);
// 5개의 데이터 저장 /////////////////////////////
LInsert(&list, 11); LInsert(&list, 11);
LInsert(&list, 22); LInsert(&list, 22);
LInsert(&list, 33);
// 저장된 데이터의 전체 출력 /////////////////////////
printf("현재 데이터의 수: %d \n", LCount(&list));
if(LFirst(&list, &data)) // 첫 번째 데이터 조회
{
printf("%d ", data);
while(LNext(&list, &data)) // 두 번째 이후의 데이터 조회
printf("%d ", data);
}
printf("\n\n");
// 숫자 22을 검색하여 모두 삭제 //////////////////////////
if(LFirst(&list, &data))
{
if(data == 22)
LRemove(&list);
while(LNext(&list, &data))
{
if(data == 22)
LRemove(&list);
}
}
// 삭제 후 남아있는 데이터 전체 출력 ////////////////////////
printf("현재 데이터의 수: %d \n", LCount(&list));
if(LFirst(&list, &data))
{
printf("%d ", data);
while(LNext(&list, &data))
printf("%d ", data);
}
printf("\n\n");
return 0;
}아직 더미 기반 연결 리스트의 모든 설명이 끝난 것은 아니다.
이어서 정렬과 관련된 설명이 이어진다.
3. 연결 리스트의 정렬 삽입의 구현
이제 정렬에 관한 부분을 설명할 차례인데 정렬의 기준을 프로그래머가 직접 결정할 수 있도록 ADT를 정의한 만큼 코드의 난이도가 약간 높을 수 있다.
우리가 구현한 연결 리스트에서 정렬기준의 설정과 관련 있는 부분은 다음과 같다.
따라서 이들은 하나로 묶어서 이해해야 한다.
- 연결 리스트의 정렬기준이 되는 함수를 등록하는 SetSortRule 함수
- SetSortRule 함수를 통해서 전달된 함수정보를 저장하기 위한 LinkedList의 멤버 comp
- comp에 등록된 정렬기준을 근거로 데이터를 저장하는 SInsert 함수위에서 언급한 세 가지를 하나의 문장으로 정리하면 다음과 같다.
"SetSortRule 함수가 호출되면서 정렬의 기준이 리스트의 멤버 comp에 등록되면,
SInsert 함수 내에서는 comp에 등록된 정렬의 기준을 근거로 데이터를 정렬하여 저장한다."이렇듯 SetSortRule 함수는 리스트의 멤버 comp를 초기화하는 함수이므로 다음과 같이 간단히 정의할 수 있다.
void SetSortRule(List * plist, int (*comp)(LData d1, LData d2))
{
plist->comp = comp;
}이어서 SInsert 함수를 소개하겠다.
이 함수도 리스트의 멤버 comp의 활용에 대한 부분이 생소할 뿐 나머지는 익숙한 코드들이다.
void SInsert(List * plist, LData data)
{
Node * newNode = (Node *)malloc(sizeof(Node)); // 새 노드의 생성
Node * pred = plist->head; // pred는 더미 노드를 가리킴
newNode->data = data; // 새 노드에 데이터 저장
while(pred->next != NULL && plist->comp(data, pred->next->data) != 0)
{
pred = pred->next; // 다음 노드로 이동
}
newNode->next = pred->next; // 새 노드의 오른쪽을 연결
pred->next = newNode; // 새 노드의 왼쪽을 연결
(plist->numOfData)++; // 저장된 데이터의 수 하나 증가
}위 함수의 반복문에서 보이듯이 comp에 등록된 함수의 호출결과를 기반으로 새 노드가 추가될 위치를 찾는다.
자! 그럼 위 함수의 동작원리를 설명하기 위해서, 다음과 같이 리스트가 구성된 상황이라고 가정하자.

위 그림은 오름차순으로 데이터가 저장된 상황이다.
이 상황에서 다음 문장이 실행된다고 가정해보자.
참고로 이 문장에서 slist는 위 그림의 리스트를 의미한다.
SInsert(&slist, 5); // 리스트에 숫자 5를 저장!위의 함수호출로 인해서 먼저 다음 세 문장이 실행된다.
Node * newNode = (Node *)malloc(sizeof(Node)); // 새 노드의 생성
Node * pred = plist->head; // pred는 더미 노드를 가리킴
newNode->data = data; // 새 노드에 데이터 저장이로 인해서 새 노드에 숫자 5가 저장되고, 다음 그림에서 보이듯이 모든 노드를 차례로 가리키기 위해 선언된 포인터 변수 pred는 더미 노드를 가리키게 된다.
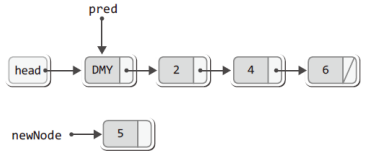
위의 그림에서 포인터 변수 pred가 숫자 2가 저장된 '첫 번째 노드'가 아닌 '더미 노드'를 가리키는 이유를 이해하겠는가?
우리는 노드를 추가할 때도 포인터 변수 pred를 활용한다.
그런데 한쪽 방향으로만 연결이 형성되어 있어서 pred가 가리키는 노드의 오른쪽에는 새 노드를 추가할 수 있어도 왼쪽에는 새 노드를 추가할 수 없다.
그래서 pred는 더미 노드부터 가리키는 것이다.
그럼 이어서 추가되는 반복문을 보자.
// 새 노드가 들어갈 위치를 찾기 위한 반복문
while(pred->next != NULL && plist->comp(data, pred->next->data) != 0)
{
pred = pred->next; // 다음 노드로 이동
}위의 반복문에 대해서는 잠시 후에 별도로 설명하겠다.
그러나 위의 반복문을 탈출하고 나면 다음 그림과 같이 pred가 가리키는 노드의 오른쪽에 새 노드가 추가되어야 한다는 사실만 인식하자.
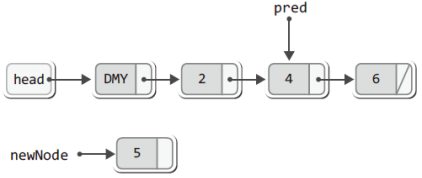
이렇듯 pred는 새노드를 추가하는데 있어서 중요한 정보를 담고 있다.
따라서 이어지는 다음 문장을 통해서 새 노드는 제자리를 찾게 된다.
newNode->next = pred->next; // 새 노드의 오른쪽을 연결
pred->next = newNode; // 새 노드의 왼쪽을 연결
(plist->numOfData)++; // 저장된 데이터의 수 하나 증가위의 문장들을 통한 추가의 과정 및 결과는 다음과 같다.
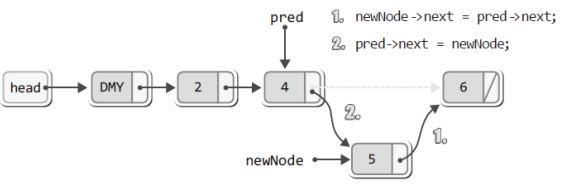
이로써 SInsert 함수의 노드 추가에 대한 큰 흐름은 모두 설명하였다.
남은 것은 SInsert 함수 내에 존재하는 정렬 삽입의 핵심이 되는 while문에 대한 이해이다.
SInsert 함수의 while문은 언뜻 복잡해 보이나 반복의 조건을 나누어 생각하면 별로 복잡하지 않다.
반복의 조건 1: pred->next != NULL
=> pred가 리스트의 마지막 노드를 가리키는지 묻기 위한 연산반복의 조건 2: plist->comp(data, pred->next->data) != 0
=> 새 데이터와 pred의 다음 노드에 저장된 데이터의 우선순위 비교를 위한 함수호출따라서 다음 반복문이 의미하는 바는,
while(pred->next != NULL && plist->comp(data, pred->next->data) != 0)
{
pred = pred->next; // 다음 노드로 이동
}다음과 같이 정리할 수 있다.
"pred가 마지막 노드를 가리키는 것도 아니고,
새 데이터가 들어갈 자리도 아직 찾지 못했다면 pred를 다음 노드로 이동시킨다."그럼 이제 우선순위 비교를 위한 다음 함수호출에 대해 설명하겠다.
plist->comp(data, pred->next->data) != 0comp에 등록된 함수가 반환하는 값은 0과 1인데, 0을 반환하면 첫 번째 인자인 data가 정렬 순서상 앞서서 head데 더 가까워야 하는 경우고, 1을 반환하면 두 번째 인자인 pred->next->data가 정렬 순서상 앞서서 head에 더 가까워야 하는 경우이다.
물론 이러한 반환 값의 종류와 그 의미는 앞서 우리가 결정한 것이다.
이제 마지막으로 남은 일은 정렬의 기준을 결정하는 함수, 다시 말해서 함수 SetSortRule의 인자가 될 수 있는 함수를 정의하는 일이다.
이 함수를 정의하는데 있어서 필요한 정보 두 가지를 정리하면 다음과 같다.
- 두 개의 인자를 전달받도록 함수를 정의한다.
- 첫 번째 인자의 정렬 우선순위가 높으면 0을, 그렇지 않으면 1을 반환한다.이 두 가지만 만족한다면 어떤 함수건 SetSortRule의 인자가 될 수 있다.
그럼 위의 두 조건을 만족하는 함수를 보이겠다.
int WhoIsPrecede(int d1, int d2)
{
if(d1 < d2)
return 0; // d1이 정렬 순서상 앞선다.
else
return 1; // d2가 정렬 순서상 앞서거나 같다.
}이는 앞서 한차례 보인 함수이다.
'오름차순 정렬'을 위한 함수라 할 수 있다.
자 이제 마지막으로 위의 함수를 추가해서 예제를 실행하여, 실제로 오름차순으로 정렬이 되는지 확인해볼 차례이다.
따라서 이와 관련된 질문을 하나 하고자 한다.
"정렬의 기준인 WhoIsPrecede 함수는 어디에 위치해야 합니까?"위 질문의 답으로 연결 리스트 구현이 담겨있는 소스파일 DLinkedList.c를 지목했다면 제대로 된 오답이다.
우리는 프로그래머가 연결 리스트의 정렬 기준을 결정하도록 유연성을 부여하지 않았는가?
따라서 연결 리스트를 활용하는, main함수가 정의되어 있는 소스파일을 지목했어야 옳다.
즉 다음과 같이 main 함수를 작성해야 한다.
DLinkedListSortMain.c
#include <stdio.h>
#include "DLinkedList.h"
int WhoIsPrecede(int d1, int d2)
{
if(d1 < d2)
return 0; // d1이 정렬 순서상 앞선다.
else
return 1; // d2가 정렬 순서상 앞서거나 같다.
}
int main(void)
{
// List의 생성 및 초기화 ////////////
List list;
int data;
ListInit(&list);
SetSortRule(&list, WhoIsPrecede);
// 5개의 데이터 저장 ///////////////
LInsert(&list, 11); LInsert(&list, 11);
LInsert(&list, 22); LInsert(&list, 22);
LInsert(&list, 33);
// 저장된 데이터의 전체 출력 ////////////
printf("현재 데이터의 수: %d \n", LCount(&list));
if(LFirst(&list, &data))
{
printf("%d ", data);
while(LNext(&list, &data))
printf("%d ", data);
}
printf("\n\n");
// 숫자 22을 검색하여 모두 삭제 ////////////
if(LFirst(&list, &data))
{
if(data == 22)
LRemove(&list);
while(LNext(&list, &data))
{
if(data == 22)
LRemove(&list);
}
}
// 삭제 후 저장된 데이터 전체 출력 ////////////
printf("현재 데이터의 수: %d \n", LCount(&list));
if(LFirst(&list, &data))
{
printf("%d ", data);
while(LNext(&list, &data))
printf("%d ", data);
}
printf("\n\n");
return 0;
}