재귀(Recursion)

1. 함수의 재귀적 호출의 이해

재귀는 자료구조와 알고리즘에 있어서 매우 중요한 요소이고, C언어는 이렇듯 중요한 재귀를 지원하는 언어이다.

재귀함수를 정의하는데 있어서 탈출조건을 구성하는 것은 매우 중요한 일이다.

---

재귀함수는 자료구조나 알고리즘의 어려운 문제를 단순화하는데 사용되는 중요한 무기이다.

무엇보다도 재귀함수가 있기에 재귀적인 수학적 수식을 그대로 코드로 옮길 수 있다.

그럼 이러한 재귀함수의 특징을 보이기 위해서 팩토리얼(factorial) 값을 반환하는 함수를 재귀적으로 구현해 보겠다.

정수 $n$의 팩토리얼은 $n!$로 표시하며, 이의 수식적 의미는 다음과 같다.

$n!\ =\ n\times \left(n-1\right)\times \left(n-2\right)\times \ ...\ \times 2\times 1$

이는 또 다음과 같이 표현될 수 있다.

$n!=n\times \left(n-1\right)!$

정수 $n$ 팩토리얼은 정수 $n$ 과 $n-1$ 팩토리얼의 곱으로 표현할 수 있으므로, $n$ 팩토리얼 $f(n)$ 은 수식적으로 다음과 같이 표현될 수 있다.

위의 식에서도 보이듯이 $f(0)$ 에 해당하는 0!이 1 이므로 이것이 재귀함수의 탈출조건이 된다.

따라서 이제 위의 식은 재귀함수를 이용해서 그대로 코드로 옮길 수 있다.

인자로 전달된 정수의 팩토리얼 값을 반환하는 함수의 이름을 Factorial이라 할 때, $n$ 이 1 이상인 경우의 수식 $n \times f(n-1)$ 은 다음과 같이 표현이 된다.

if(n>=1)
    return n*Factorial(n-1);

그리고 $n$ 이 0인 경우 결과값 1은 다음과 같이 표현이 된다.

if(n==0)
    return 1;

따라서 Factorial 함수에 0이상의 값만 전달된다는 가정을 하면, 위의 두 if문은 다음과 같이 하나의 if-else문으로 묶을 수 있다.

if(n==0)
    return 1;
else
    return n*Factorial(n-1)

이로써 팩토리얼 값을 반환하는 Factorial 함수를 완성한 셈이다.

그럼 전체 코드를 통해 팩토리얼이 정확히 출력이 되는지 확인해보자.

#include <stdio.h>

int Factorial(int num)
{
	if(num==0)
		return 1;
	else
		return num * Factorial(num-1);
}

int main(void)
{
	int num=3;
	
	printf("%d", Factorial(num)); //6
	
	return 0;
}

---

2. 재귀의 활용

피보나치 수열은 재귀적인 형태를 띠는 대표적인 수열로서 다음과 같이 전개가 된다.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

흔히 하는 말로 '앞엣걸 두 개 더해서 현재의 수를 만들어가는 수열'이다.

때문에 처음 두 개의 수 0과 1이 주어진 상태에서 수를 만들어가 가게 된다.

첫 번째, 두 번째 값 0과 1을 더해서 세 번째 값 1이 결정된다.

그리고 두 번째, 세 번째 값 1과 1을 더해서 네 번째 값 2가 결정된다.

이렇듯 수열의 첫 번째와 두 번째가 아닌 n번째 값은 다음과 같이 결정된다.

$수열의\ n번째\ 값=\ 수열의\ n-1번째\ 값+수열의\ n-2번째\ 값$

따라서 피보나치 수열의 n번째 위치의 값을 반환하는 함수는 수학적으로 다음과 같이 표현이 된다.

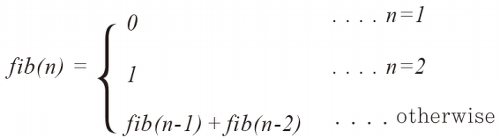
그럼 이를 코드로 옮겨보겠다.

int Fibo(int n)
{
	if(n==1)
		return 0;
	else if(n==2)
		return 1;
	else
		return Fibo(n-1) + Fibo(n-2);
}

중요한 것은 수학적 재귀의 표현이 그대로 코드로 옮겨졌음을 인식하는 것이다.

그럼 전체 코드를 통해 위 함수가 제대로 정의된 것인지 확인해보자.

#include <stdio.h>

int Fibo(int n)
{
	if(n==1)
		return 0;
	else if(n==2)
		return 1;
	else
		return Fibo(n-1) + Fibo(n-2);
}

int main(void)
{
	int num=5;
	
	printf("피보나치 수열의 %d번째 값: %d", num, Fibo(num));
	
	return 0;
}

위 코드에서 else 부분에 있는 'Fibo(n-1) + Fibo(n-2)'는 + 연산자의 왼편에 있는 Fibo 함수호출이 완료되어야 비로소 + 연산자의 오른편에 있는 Fibo 함수호출이 진행이 된다.

때문에 다음의 순서대로 재귀적으로 함수의 호출이 진행된다.

참고로 그림 안에 쓰여진 숫자는 함수의 호출순서를 의미한다.

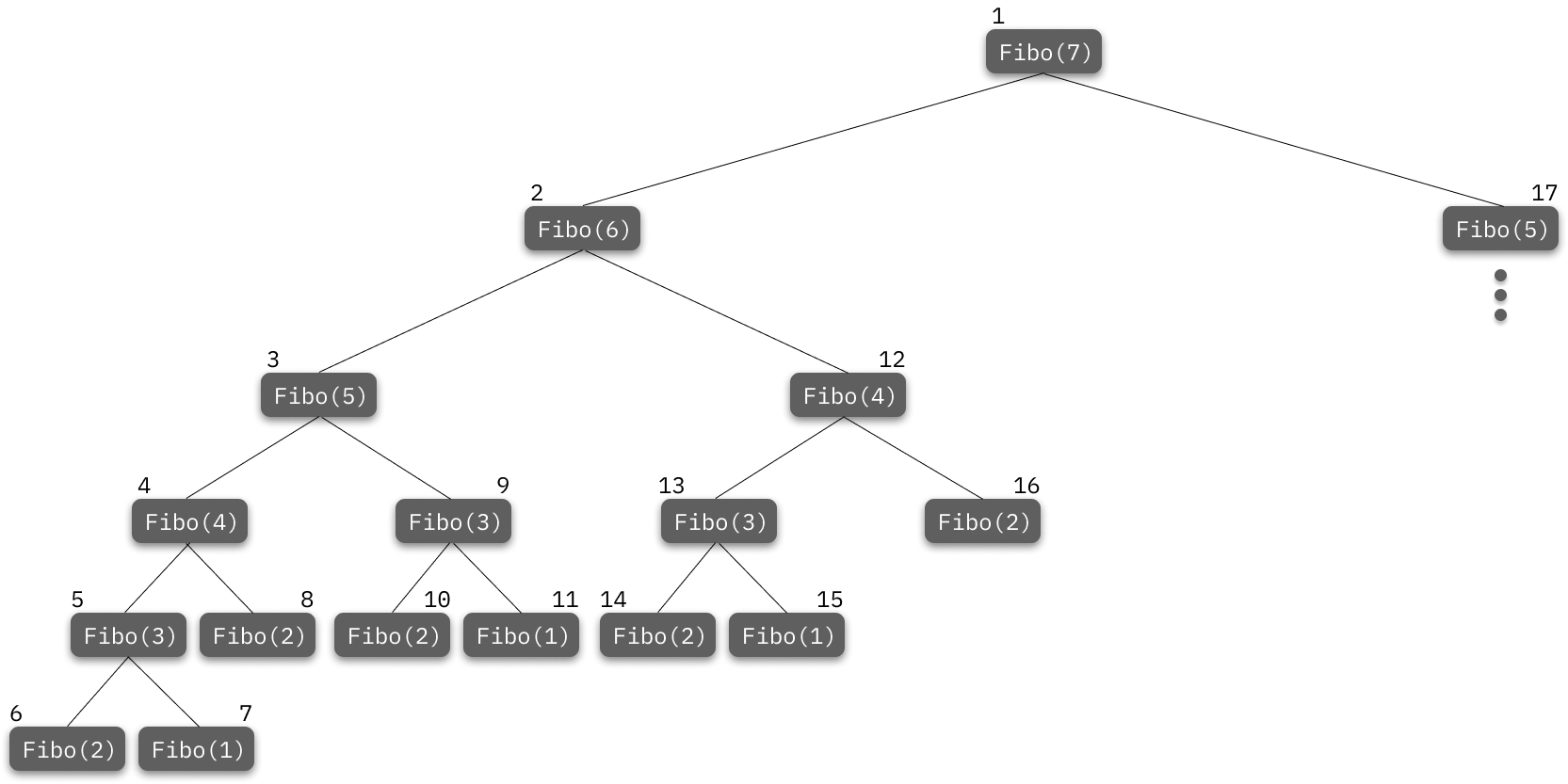
재귀함수의 호출순서를 정리하는 것은 한번이면 족하다.

이는 호출되는 순서를 정리하는 것이 큰 의미가 없음을 뜻한다.

---

이번에는 앞서 구현한 이진 탐색 알고리즘을 재귀함수 기반으로 재구현하고자 한다.

이 알고리즘을 수식적으로 표현하기는 부적절하지만 알고리즘의 논리 자체는 재귀적이기 때문에 충분히 가능한 일이다.

#include <stdio.h>

int BSearchRecur(int arr[], int first, int last, int target)
{
	if(first>last)
		return -1; // -1의 반환은 탐색의 실패를 의미 
		
	int mid=(first+last)/2; // 탐색 대상의 중앙을 찾는다 
	
	if(arr[mid]==target)
		return mid; // 탐색된 인덱스 반환 
	else if(target<arr[mid])
		return BSearchRecur(arr, first, mid-1, target);
	else
		return BSearchRecur(arr, mid+1, last, target);
}

int main(void)
{
	int arr[5]={1,3,5,7,9};
	int idx;
	
	idx=BSearchRecur(arr, 0, sizeof(arr)/sizeof(int)-1, 9);
	
	if(idx==-1)
		puts("탐색 실패");
	else
		printf("타겟 인덱스: %d", idx);
	
	return 0;
}

이로써 이진 탐색 알고리즘을 재귀함수 기반으로 구현 완료하였다.

"그런데 이진 탐색 알고리즘을 굳이 재귀함수 기반으로 구현하는 이유가 뭔가요?"

재귀함수에 익숙해지는데 그 목적이 있다.

아직은 반복문을 기반으로 구현된 코드가 익숙하게 느껴질 것이지만 재귀함수를 기반으로 구현된 위의 코드도 자연스럽게 이해할 수 있을 정도가 되어야 한다.

그래야 끝까지 공부하는데 부담이 없다.