탐색(Search) 2

1. 균형 잡힌 이진 탐색 트리: AVL 트리의 이해

앞 챕터에서 소개한 이진 탐색 트리는 그 자체만으로도 매력적이지만, 그럼에도 불구하고 나름의 단점을 지니고 있다.

따라서 이번에는 이진 탐색 트리의 단점을 개선한 또 다른 이진 탐색 트리를 소개하고자 한다.

---

이진 탐색 트리의 탐색 연산은 $O(log n)$의 시간 복잡도를 가진다.

트리의 높이를 하나씩 더해갈수록 추가할 수 있는 노드의 수가 두 배씩 증가하므로, 이진 탐색 트리의 빅-오는 별도의 계산을 거치지 않고서도 이렇듯 쉽게 판단이 가능하다.

그런데 이러한 이진 탐색 트리는 균형이 맞지 않을수록 $O(n)$에 가까운 시간 복잡도를 보인다.

이와 관련해서 다음 그림을 보자.

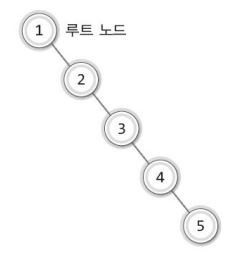
위의 그림에서는 1부터 5까지의 정수가 순서대로 저장되었을 때의 이진 탐색 트리를 보여준다.

이는 분명 이진 탐색 트리의 조건을 만족한다.

그럼에도 불구하고 노드의 수에 가까운 높이를 형성했다.

반면 1부터 5까지의 정수를 순서대로 저장하되 3만 제일 먼저 저장을 해도 결과는 다음과 같이 달라진다.

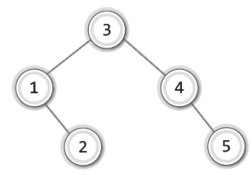
위 그림에서 보이듯이, 저장 순서만 조금 바꿨더니 루트 노드를 기준으로 어느 정도 균형이 잡혔고 트리의 높이도 반으로 줄었다.

이렇듯 앞서 구현한 이진 탐색 트리는 저장 순서에 따라 탐색의 성능에 큰 차이를 보인다.

그리고 이것이 이진 탐색 트리의 단점이다!

이러한 이진 탐색 트리의 단점을 해결한 트리를 가리켜 '균형 잡힌 이진 트리'라 하며, 그 종류는 대략 다음과 같다.

- AVL 트리

- 2-3 트리

- 2-3-4 트리

- Red-Black 트리

- B 트리

이 중에서 하나를 선택하여 우리가 구현한 '이진 탐색 트리'가 자동으로 균형을 잡을 수 있도록 개선해보고자 한다.

그리고 그러한 목적으로 여기서는 AVL 트리를 선택하였다!

---

AVL 트리는 1960년대에 고안되었으며 이 때 고안한 사람들의 이름을 따서 정해졌다.

AVL 트리는 노드가 추가될 때, 그리고 삭제될 때 트리의 균형상태를 파악해서 스스로 그 구조를 변경하여 균형을 잡는 멋진 트리이다.

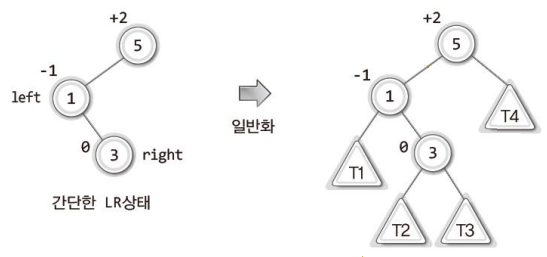
AVL 트리에서는 균형의 정도를 표현하기 위해서 '균형 인수(Balance Factor)'라는 것을 사용하는데, 이 균형 인수는 다음과 같이 계산된다.

균형 인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이

그럼 다음 그림에서 보이는 두 이진 트리의 각 노드 별 균형 인수를 확인해보자.

노드 위에 적힌 숫자가 '균형 인수'이다.

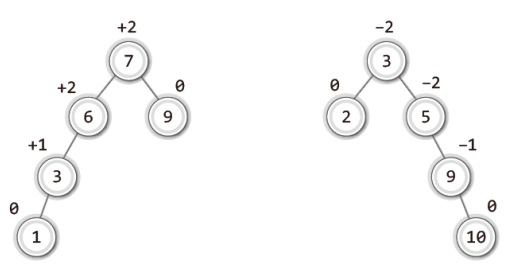
균형 인수에 대해 알았으니, AVL 트리의 리밸런싱(rebalancing) 시기를 짐작할 수 있을 것이다.

균형 인수의 절댓값이 크면 클수록 그만큼 트리의 균형이 무너진 상태이다.

따라서 AVL 트리는 균형 인수의 절댓값이 2 이상인 경우에 균형을 잡기 위한 트리의 재조정을 진행한다.

---

AVL 트리의 균형이 무너지는 상태는 4가지로 정리가 된다.

그리고 각 상태 별 리밸런싱 방법에도 차이가 있다.

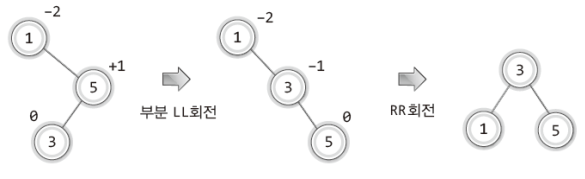
그 중 첫 번째 상태는 다음과 같다.

위 그림의 왼편을 보면 루트 노드의 균형 인수가 +2이다.

이렇듯 균형 인수 +2가 연출된 이 상황을 다음과 같이 표현할 수 있다.

"5가 저장된 노드의 왼쪽에 3이 저장된 자식 노드가 하나 존재하고,

그 자식 노드의 왼쪽에 1이 저장된 자식 노드가 또 하나 존재한다."

사실 이는 매우 엉성한 표현이다.

하지만 이 엉성한 표현을 다시 보자.

그럼 다음 사실을 알 수 있다.

"핵심은 자식 노드 두 개가 왼쪽으로 연이어 연결되어서 균형 인수 +2가 연출되었다는 것이다!"

따라서 균형 인수 +2가 연출된 이 상태를 가리켜 'Left Left 상태' 줄여서 'LL상태'라 한다.

그리고 이러한 LL상태에서 발생한 불균형의 해소를 위해 등장한 리밸런싱 방법을 가리켜 'LL회전'이라 한다.

즉 LL회전이란 왼쪽으로 두 번 돌리는 회전을 의미하는 것이 아니고, LL상태에서 균형을 잡기 위해 필요한 회전을 의미하는 것이다.

위 그림의 오른편에서는 LL회전의 방법과 그 결과를 보이고 있다.

LL회전의 핵심은 균형 인수가 +2인 노드를 균형 인수가 +1인 노드의 오른쪽 자식 노드가 되게 하는데 있다.

그럼 다음 그림을 대상으로 LL회전의 방법을 코드로 정리해 보겠다.

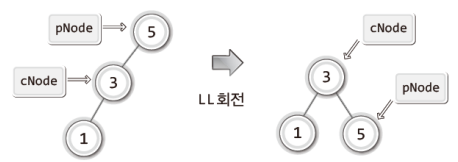
위 그림에서 보이듯이 pNode와 cNode가, 각각 균형 인수가 +2인 노드와 그 자식 노드를 가리킨다고 가정하면, 앞 챕터에서 완성한 BinaryTree3.c에 정의된 함수를 도구로 하여 다음 한 문장으로 LL회전으로 완성할 수 있다.

ChangeRightSubTree(cNode, pNode);

하지만 다음 그림에서 보이는 LL상태까지 고려한다면 위의 한 문장만으로는 부족하다.

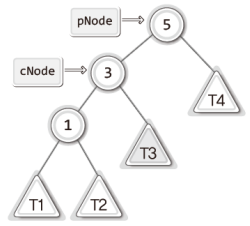
위 그림의 T1, T2, T3, T4를 높이가 동일한 서브 트리라고 가정해보자.

그렇다면 이들은 5가 저장된 노드와 3이 저장된 노드의 균형 인수에 영향을 미치지 않는다.

때문에 이 그림의 구조 역시 LL상태에 해당한다.

그리고 T1, T2, T3, T4를 NULL로 치환하면, 이는 앞서 보인 LL상태가 된다.

때문에 이는 LL상태를 일반화한 것으로 볼 수 있다.

그럼 위의 상태에서 LL회전을 위해 추가로 고민해야 할 것은 무엇인가?

그것은 T3이다.

사실 T1, T2 그리고 T4는 고민하지 않아도 된다.

이들은 이들의 부모 노드가 이동을 하면서 늘 붙어 다니기 때문이다.

그리고 붙어 다닌다고 해서 문제가 되지도 않는다.

하지만 T3는 다르다.

T3의 부모 노드는 루트 노드가 될 분이시다.

따라서 T3는 그 자리를 다른 노드에게 양보해야 한다.

위 그림을 기준으로 본다면 5가 저장된 노드에게 양보해야 한다.

그럼 T3는 어디로 가야 하는가? 5가 저장된 노드에게 자리를 양보하고 나면 남는 자리가 보인다.

그것은 5가 저장된 노드의 왼쪽 자식 노드의 위치이며, 이 자리로 이동했을 때에도 여전히 이진 탐색 트리의 기준에 부합한다.

그럼 회전의 결과를 보이겠다.

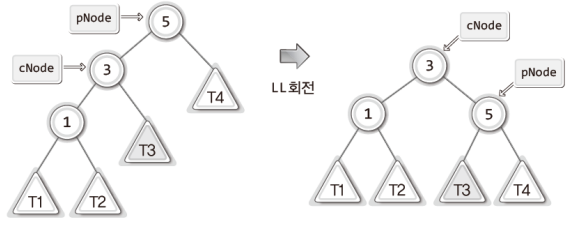
위 그림에서 보이듯이 cNode가 가리키는 노드의 오른쪽 서브 트리를 pNode가 가리키는 노드의 왼쪽 서브 트리로 옮기기 위해서는 다음 문장을 실행해야 한다.

ChangeLeftSubTree(pNode, GetRightSubTree(cNode));

정리하면, LL회전을 위해서는 다음 두 문장을 순서대로 실행해야 한다.

ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
ChangeRightSubTree(cNode, pNode);

LL회전과 관련하여 위의 두 문장이 필요한 이유와 각각의 역할을 이해했다면, 잠시 후에 보이는 LL회전을 담당하는 함수는 이해한 것이나 다름이 없다.

---

LL상태와 LL회전에 대해서 이야기했으니, 이번에 설명하는 RR상태와 RR회전에 대해서는 쉽게 이야기를 풀어갈 수 있다.

"RR상태와 LL상태의 차이점, 그리고 RR회전과 LL회전의 유일한 차이점은 방향 아닌가요"

그렇다! 유일한 차이점은 방향이다.

LL상태가 왼쪽으로 길게 늘어진 모습을 보인다면, RR상태는 오른쪽으로 길게 늘어진 모습을 보인다.

그럼 이어서, RR상태와 이를 균형잡기 위한 RR회전을 보이겠으니, 이를 LL회전과 비교하여 이해해보자.

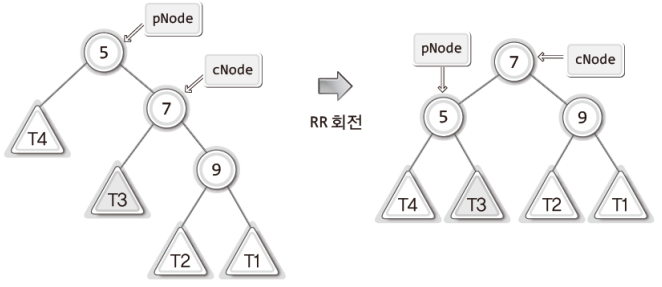
위 그림에서 주목할 것 두 가지는 다음과 같다.

- 5가 저장된 노드가 7이 저장된 노드의 왼쪽 자식 노드가 되었다.

- T3는 5가 저장된 노드의 오른쪽 서브 트리가 되었다.

이름 pNode와 cNode를 기준으로 코드로 표현하면 다음과 같다.

ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
ChangeLeftSubTree(cNode, pNode);

ChangeLeftSubTree가 선행된다면, cNode의 왼쪽 서브 트리의 주소 값을 잃게 되기 때문에 cNode의 왼쪽 서브 트리의 이동이 우선이다.

앞서 LL회전에서도 마찬가지다.

---

LL회전, RR회전에 이어 LR회전을 알아볼 차례이다.

LR상태는 다음과 같은 상태를 뜻한다.

그리고 LR회전은 이러한 상태에서의 리밸런싱 방법을 뜻한다.

그렇다면 LR회전은 어떻게 해야 하는 것일까?

LR상태는 앞서 보인 LL상태나 RR상태보다 균형을 잡기가 복잡하다.

한 번의 회전으로 균형을 잡을 수 없기 때문이다.

따라서 다음과 같은 방법을 취해야 한다.

"LR상태를 LL상태나 RR상태로 일단 바꾼다."

알다시피 LL상태나 RR상태로 바꾸고 나면, 이후의 리밸런싱 과정은 비교적 단순하다.

그렇다면 어떻게 LL상태나 RR상태로 바꿀 수 있을까?

결론부터 말하겠다.

"LR상태에는 RR회전을 통해서 LL상태가 되게 할 수 있다."

이는 RR회전의 부수적인 효과를 이용한 것으로 볼 수 있는데, 이에 대한 설명을 위해서 앞서 보인 RR회전의 결과를 다시 한 번 관찰하자.

위의 그림에서 9가 저장된 노드를 NULL로 치환하면 다음의 상태가 된다.

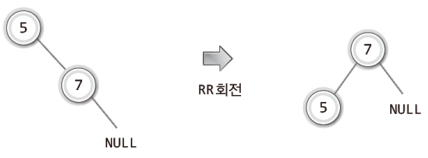
실제로 위 그림의 상황에서도 RR회전이 가능하다.

물론 이러한 형태의 RR회전은 균형을 잡기 위한 트리 구조의 재조정과는 거리가 있다.

하지만 RR회전을 통해서 5와 7이 저장된 두 노드의 관계를 다음과 같이 바꿔 놓을 수 있다.

위 그림에서 보이듯이 부모 노드와 자식 노드의 관계가 바뀌었다.

더불어서 오른쪽으로 형성되었던 부모와 자식의 관계가 왼쪽으로 바뀌었다.

그리고 이것이 바로 RR회전을 통해서 우리가 얻을 수 있는 부수적인 효과이다.

그럼 다시 본론으로 돌아와서 다음 그림을 보자.

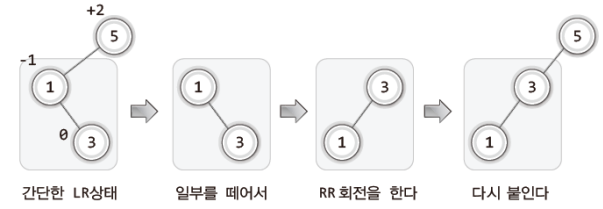
위 그림은 앞서 설명한 RR회전의 부수적인 효과를 이용하여, LR상태를 LL상태로 바꾸는 과정을 보여준다.

물론 이렇게 바뀐 LL상태도 이진 탐색 트리의 기본 조건을 만족한다.

따라서 이제 남은 것은 위의 결과를 대상으로 LL회전을 시켜서 트리의 균형을 잡는 일이다.

그리고 그 과정을 정리하면 다음과 같다.

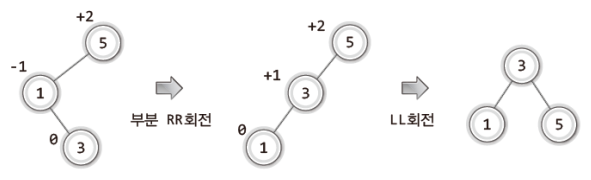
위 그림에서 보이듯이 LR회전은 부분적 RR회전과 LL회전의 조합으로 이뤄진다.

실제로 잠시 후에 보일 LR회전을 담당하는 함수는, 내부적으로 RR회전을 담당하는 함수와 LL회전을 담당하는 함수를 호출한다.

그리고 이 사실만 알고 있어도 LR회전을 담당하는 함수는 쉽게 이해할 수 있다.

따라서 LR회전과 관련된 코드는 잠시 후에 확인하기로 하겠다.

---

마지막으로 RL상태가 남았는데, 이 RL상태는 자식 노드가 연결된 방향이 LR상태와 반대일 뿐이다.

따라서 과정도 LR상태일 때와 정확히 반대의 과정을 거쳐주면 리밸런싱이 완료된다.

그럼 바로 RL상태의 트리를, RR상태로 바꾸는 과정을 보이겠다.

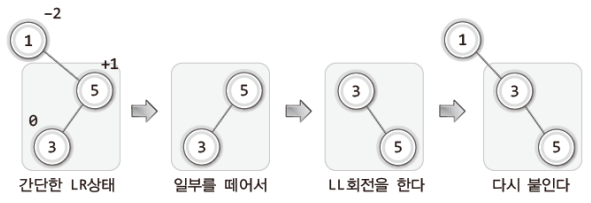
마지막으로 RL회전의 전체과정을 보이겠으니, 앞서 보인 LR회전의 전체과정과 비교하여 이 둘의 차이점을 확인해보자.

---

2. 균형 잡힌 이진 탐색 트리: AVL 트리의 구현

AVLRebalance.h

#ifndef __AVL_REBALANCE_H__
#define __AVL_REBALANCE_H__

#include "BinaryTree3.h"

// 트리의 균형을 잡는다.
BTreeNode * Rebalance(BTreeNode ** pRoot);

#endif

---

AVLRebalance.c

#include <stdio.h>
#include "BinaryTree3.h"

// LL 회전
BTreeNode * RotateLL(BTreeNode * bst)
{
	BTreeNode * pNode;
	BTreeNode * cNode;

	pNode = bst;
	cNode = GetLeftSubTree(pNode);

	ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
	ChangeRightSubTree(cNode, pNode);
	return cNode;
}

// RR 회전
BTreeNode * RotateRR(BTreeNode * bst)
{
	BTreeNode * pNode;
	BTreeNode * cNode;

	pNode = bst;
	cNode = GetRightSubTree(pNode);

	ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
	ChangeLeftSubTree(cNode, pNode);
	return cNode;
}

// RL 회전
BTreeNode * RotateRL(BTreeNode * bst)
{
	BTreeNode * pNode;
	BTreeNode * cNode;

	pNode = bst;
	cNode = GetRightSubTree(pNode);

	ChangeRightSubTree(pNode, RotateLL(cNode));   // 부분적 LL 회전
	return RotateRR(pNode);     // RR 회전
}

// LR 회전
BTreeNode * RotateLR(BTreeNode * bst)
{
	BTreeNode * pNode;
	BTreeNode * cNode;

	pNode = bst;
	cNode = GetLeftSubTree(pNode);
	
	ChangeLeftSubTree(pNode, RotateRR(cNode));   // 부분적 RR 회전
	return RotateLL(pNode);     // LL 회전
}

// 트리의 높이를 계산하여 반환
int GetHeight(BTreeNode * bst) 
{
	int leftH;		// left height
	int rightH;		// right height

	if(bst == NULL)
		return 0;

	// 왼쪽 서브 트리 높이 계산
	leftH = GetHeight(GetLeftSubTree(bst));

	// 오른쪽 서브 트리 높이 계산
	rightH = GetHeight(GetRightSubTree(bst));

	// 큰 값의 높이를 반환한다.
	if(leftH > rightH)
		return leftH + 1;
	else
		return rightH + 1;
}

// 두 서브 트리의 높이의 차를 반환
int GetHeightDiff(BTreeNode * bst)
{
	int lsh;    // left sub tree height
	int rsh;    // right sub tree height

	if(bst == NULL)
		return 0;

	lsh = GetHeight(GetLeftSubTree(bst));
	rsh = GetHeight(GetRightSubTree(bst));

	return lsh - rsh;
}

// 트리의 균형을 잡는다.
BTreeNode * Rebalance(BTreeNode ** pRoot)
{
	int hDiff = GetHeightDiff(*pRoot);

	if(hDiff > 1)     // 왼쪽 서브 트리 방향으로 높이가 2 이상 크다면
	{
		if(GetHeightDiff(GetLeftSubTree(*pRoot)) > 0)
			*pRoot = RotateLL(*pRoot);
		else
			*pRoot = RotateLR(*pRoot);
	}
	
	if(hDiff < -1)     // 오른쪽 서브 트리 방향으로 2 이상 크다면
	{
		if(GetHeightDiff(GetRightSubTree(*pRoot)) < 0)
			*pRoot = RotateRR(*pRoot);
		else
			*pRoot = RotateRL(*pRoot);
	}
	
	return *pRoot;
}

---

AVLTreeMain.c

#include <stdio.h>
#include "BinaryTree3.h"	// 트리의 구조를 확인하기 위해서
#include "BinarySearchTree3.h"

int main(void)
{
	BTreeNode * avlRoot;
	BTreeNode * clNode;		// current left node
	BTreeNode * crNode;		// current right node
    
	BSTMakeAndInit(&avlRoot);

	BSTInsert(&avlRoot, 1);
	BSTInsert(&avlRoot, 2);
	BSTInsert(&avlRoot, 3);
	BSTInsert(&avlRoot, 4);
	BSTInsert(&avlRoot, 5);
	BSTInsert(&avlRoot, 6);
	BSTInsert(&avlRoot, 7);
	BSTInsert(&avlRoot, 8);
	BSTInsert(&avlRoot, 9);

	printf("루트 노드: %d \n", GetData(avlRoot)); //4

	clNode = GetLeftSubTree(avlRoot);
	crNode = GetRightSubTree(avlRoot);
	printf("왼쪽1: %d, 오른쪽1: %d \n", GetData(clNode), GetData(crNode)); //2, 6

	clNode1 = GetLeftSubTree(clNode);
	crNode1 = GetRightSubTree(clNode);
	printf("왼쪽2: %d, 오른쪽2: %d \n", GetData(clNode), GetData(crNode)); //1, 3

	clNode2 = GetLeftSubTree(crNode);
	crNode2 = GetRightSubTree(crNode);
	printf("왼쪽3: %d, 오른쪽3: %d \n", GetData(clNode), GetData(crNode)); //5, 8

	clNode3 = GetLeftSubTree(crNode2);
	crNode3 = GetRightSubTree(crNode2);
	printf("왼쪽4: %d, 오른쪽4: %d \n", GetData(clNode), GetData(crNode)); //7, 9
    
	return 0;
}