Chapter 5 관계 데이터 모델

01. 관계 데이터 모델의 개념

1. 관계 데이터 모델의 기본 용어

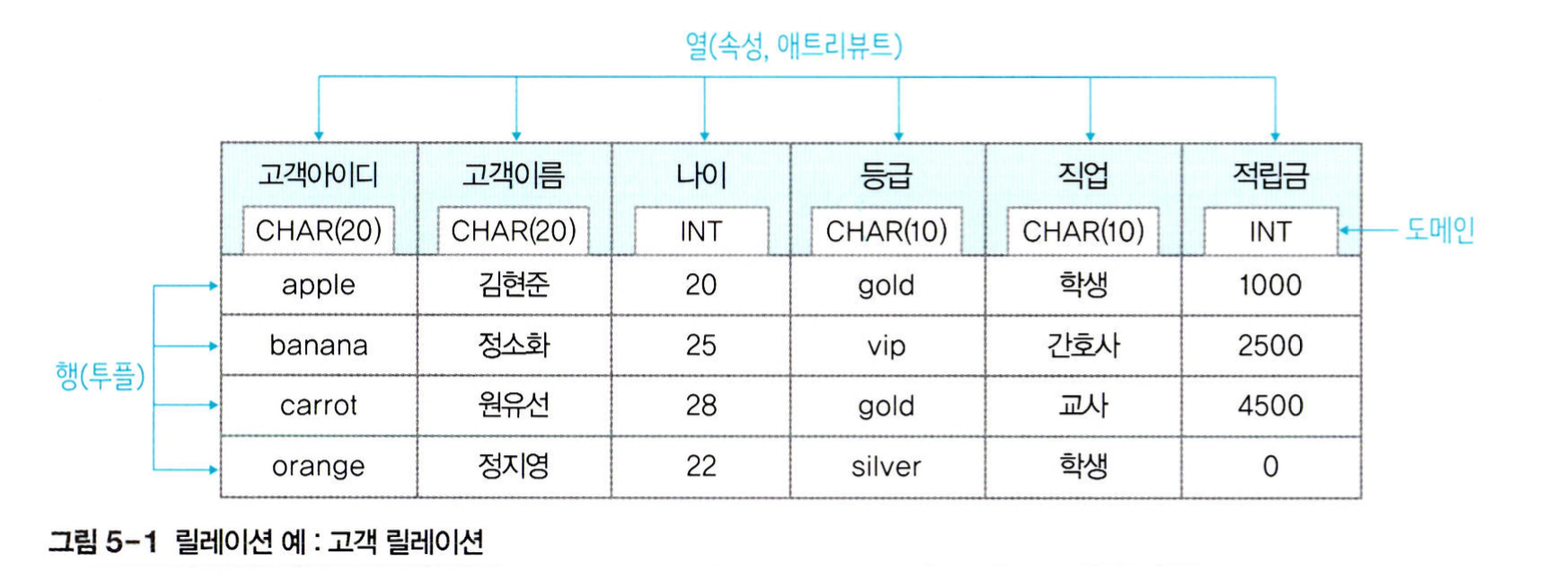
일반적으로 관계 데이터 모델에서는 하나의 개체에 관한 데이터를 릴레이션 하나에 담아 데이터베이스에 저장합니다.
위 그림은 인터넷 쇼핑몰을 위한 데이터베이스에서 고객 개체를 표현한 고객 릴레이션입니다. 이 예제를 통해 릴레이션에 관련된 용어를 알아보도록 하겠습니다.

속성

• 릴레이션의 열을 속성 또는 Attribute라고 부릅니다.
• 위 사진에서는 고객아이디, 고객이름, 나이 등에 해당합니다.

투플

• 릴레이션의 행을 투플이라고 부릅니다.
• 위 사진에서는 고객 한명에 대한 실제 속성 값 6개를 모아놓은 것으로, 고객 개체의 인스턴스입니다.

도메인

• 속성 하나가 가질 수 있는 모든 값의 집합을 해당 속성의 도메인이라고 합니다.
• 고객 릴레이션에서, 등급 속성의 값으로 vip, gold, silver, bronze 중 하나만 허용된다면, 네 가지 값을 모아놓은 것이 등급 속성의 도메인이 됩니다.

차수

• 하나의 릴레시션에서 속성의 전체 개수를 릴레이션의 차수(degree)라고 합니다.
• 위 사진에서의 고객 릴레이션은 차수가 6입니다.
• 릴레이션의 차수는 일반적으로 자주 변하지 않는다는 정적인 특징이 있습니다.

카디널리티

• 하나의 릴레이션에서 투플의 전체 개수를 릴레이션의 카디널리티라고 합니다.
• 위 사진에서 고객 릴레이션의 카디널리티는 4 입니다.

2. 릴레이션과 데이터베이스의 구성

관계 데이터 모델에서, 릴레이션은 릴레이션 스키마와 릴레이션 인스턴스로 구성되어 있습니다.

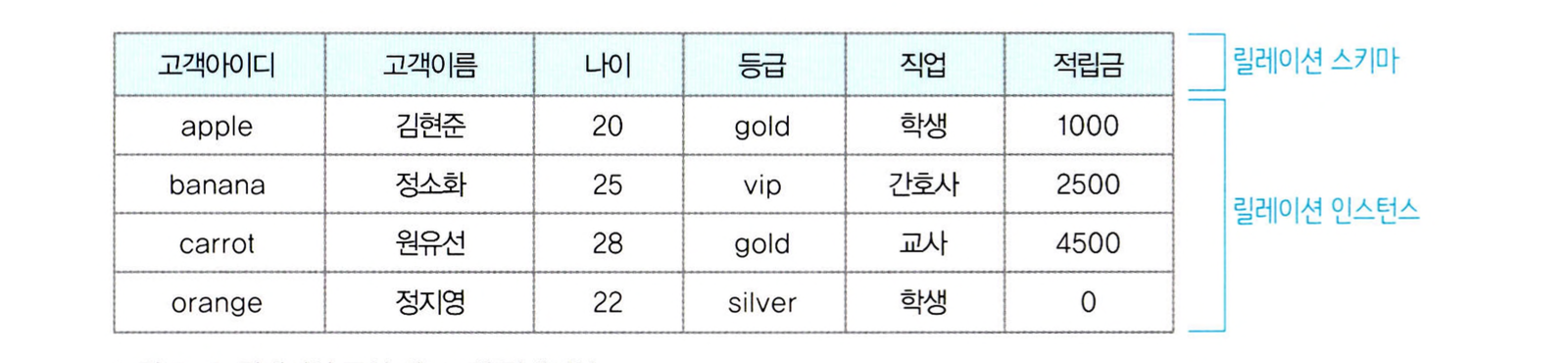
릴레이션 스키마
릴레이션 스키마는 릴레이션의 이름과 릴레이션에 포함된 모든 속성의 이름으로 정의하는 릴레이션의 논리적 구조입니다. 릴레이션 스키마는 일반적으로 다음과 같이 표현됩니다.

릴레이션이름(속성이름1, 속성이름2, ... , 속성이름n)

릴레이션 스키마를 보면 릴레이션의 이름이 무엇이고, 어떤 속성들로 구성되어 있는지 전체 구조를 쉽게 파악할 수 있습니다. 릴레이션 스키마는 릴레이션 내포라고도 부릅니다.

릴레이션 인스턴스
릴레이션 인스턴스는 어느 한 시점에 릴레이션에 존재하는 투플들의 집합입니다. 릴레이션 인스턴스에 포함된 투플은 릴레이션 스키마에서 정의하는 각 속성에 대응하는 실제 값으로 구성되어 있습니다.
릴레이션 인스턴스는 간단하게 릴레이션이라고 부르기도 하고, 릴레이션 외연이라고도 부릅니다.
릴레이션 스키마는 자주 변하지 않지만, 릴레이션 인스턴스는 투플의 삽입, 삭제, 수정이 자주 발생한다는 동적인 특징이 있습니다.

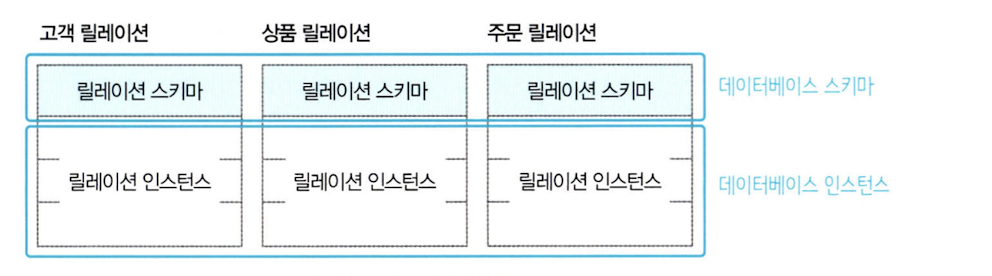
데이터베이스 스키마와 데이터베이스 인스턴스
일반적으로 데이터베이스는 릴레이션 여러개로 구성됩니다. 예를 들어, 인터넷 쇼핑몰을 위한 데이터베이스는 고객 릴레이션, 상품 릴레이션, 주문 릴레이션으로 구성할 수 있습니다.

3. 릴레이션의 특성

관계 데이터 모델의 릴레이션에는 네 가지 중요한 특성이 있습니다.

투플의 유일성 :

• 하나의 릴레이션에는 동일한 투플이 존재할 수 없다.
• 하나의 릴레이션에 똑같은 투플이 있으면 안되고, 모든 투플에는 다른 투플과 구별되는 유일한 특성이 있어야 합니다.

투플의 무순서 :

• 하나의 릴레이션에서 투플 사이의 순서는 무의미하다.
• 투플 순서가 바뀐다고 다른 릴레이션이 될 수 없고, 순서와 상관없이 투플 내용이 같아야 같은 릴레이션입니다.

속성의 무순서

• 하나의 릴레이션에서 속성 사이의 순서는 무의미하다.
• 속성의 순서가 바뀌어도 다른 릴레이션이 될 수 없고, 순서와 상관없이 같은 속성들로 구성되어 있어야 같은 릴레이션입니다.

속성의 원자성

• 속성 값으로 원자값만 가용할 수 있다.
• 모든 속성 값은 더는 분해할 수 없는 하나의 값, 즉 원자 값만 가질 수 있습니다.

4. 키의 종류

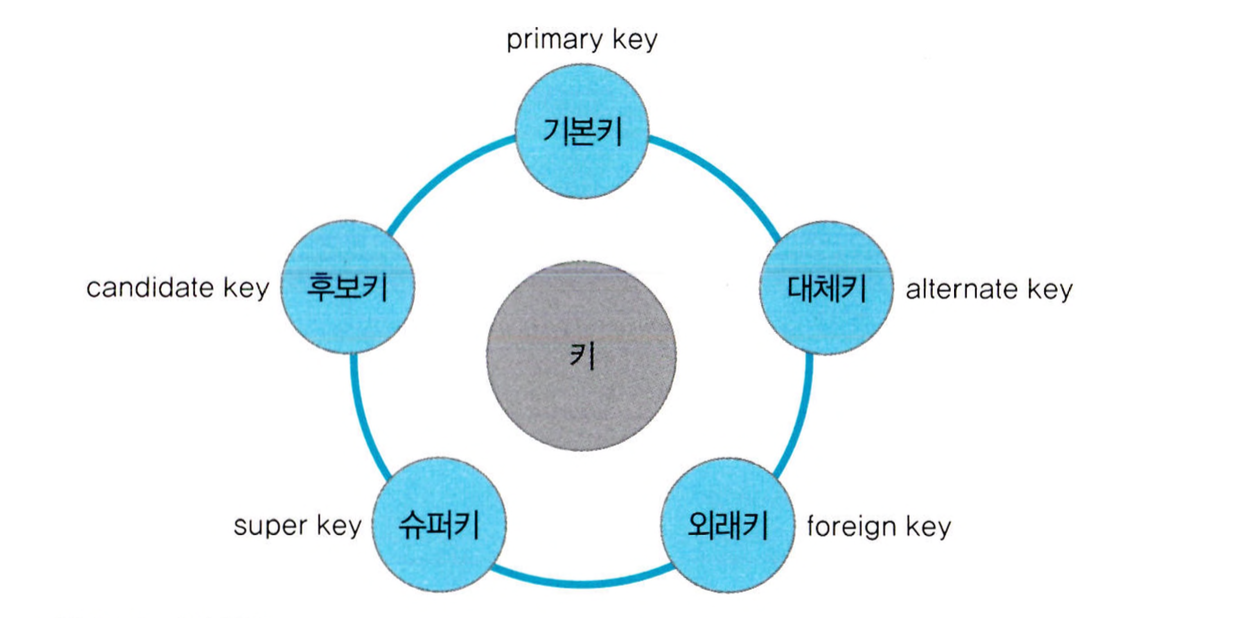
키의 특성

• 유일성 : 하나의 릴레이션에 모든 투플은 서로 다른 키값을 가져야 한다.
• 최소성 : 꼭 필요한 최소한의 속성들로만 키를 구성

슈퍼키

• 유일성의 특성을 만족하는 속성 또는 속성들의 집합
• 하나의 릴레이션에서 키로 지정된 속성 값은 투플마다 달라야 합니다.

후보키

• 유일성과 최소성을 만족하는 속성 또는 속성들의 집합

기본키

• 투플을 구별하기 위해 여러 개의 후보키를 모두 사용할 필요는 없습니다.
• 여러 후보키 중에서 기본적으로 사용할 키를 반드시 선택해야 하는데, 이것이 기본키입니다.

기본키로 채택되기 위해서는 다음 세 가지 조건을 충족해야 합니다.
1. 널 값을 가질 수 있는 속성이 포함된 후보키는 기본키로 부적합
2. 값이 자주 변경될 수 있는 속성이 포함된 후보키는 기본키로 부적합
3. 단순한 후보키를 기본키로 선택

대체키

• 기본키로 선택되지 못한 후보키들이 대체키가 됩니다.

외래키

• 어떤 릴레이션에 소속된 속성 또는 속성 집합이 다른 릴레이션의 기본키다 되는 키 입니다.

02. 관계 데이터 모델의 제약

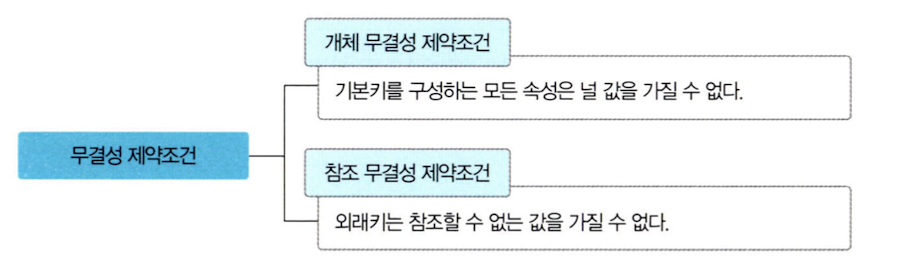
1. 개체 무결성 제약조건

개체 무결성 제약조건은 기본키를 구성하는 모든 속성은 널 값을 가지면 안된다는 규칙입니다.
관계 데이터 모델에서는 릴레이션에 포함된 투플들을 유일하게 구별해주고, 각 투플에 쉽게 접근할 수 있도록 릴레이션마다 기본키를 정의합니다. 그런데 기본키를 구성하는 속성 전체나 일부가 널 값이 되면 투플의 유일성을 판단할 수 없어 기본키의 본래 목적을 상실하게 됩니다.

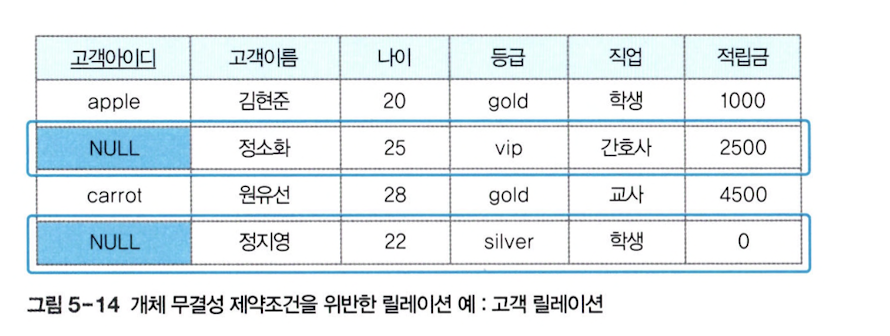
위 사진은, 투플에서 기본키인 고객 아이디 속성의 값이 널입니다. 널 값은 아직 결정되지 않았거나 모르는 값을 의미하기 떄문에, 이 경우에는 정소화 고객과 정지영 고객의 아이디가 다른 고객의 아이디와 다른지를 판단하기 어렵습니다.

2. 참조 무결성 제약조건

참조 무결성 제약조건은 외래키에 대한 규칙으로 연관된 릴레이션들에 적용됩니다.
참조 무결성 제약조건이란 외래키는 참조할 수 없는 값을 가질 수 없다는 규칙입니다.
외래키가 자신이 참조하는 릴레이션의 기본키와 상관이 없는 값을 가지게 되면 두 릴레이션을 연관시킬 수 없으므로 외래키 본래의 의미가 없어집니다. 다음 사진은 참조 무결성 제약 조건을 위반한 릴레이션의 예시입니다.

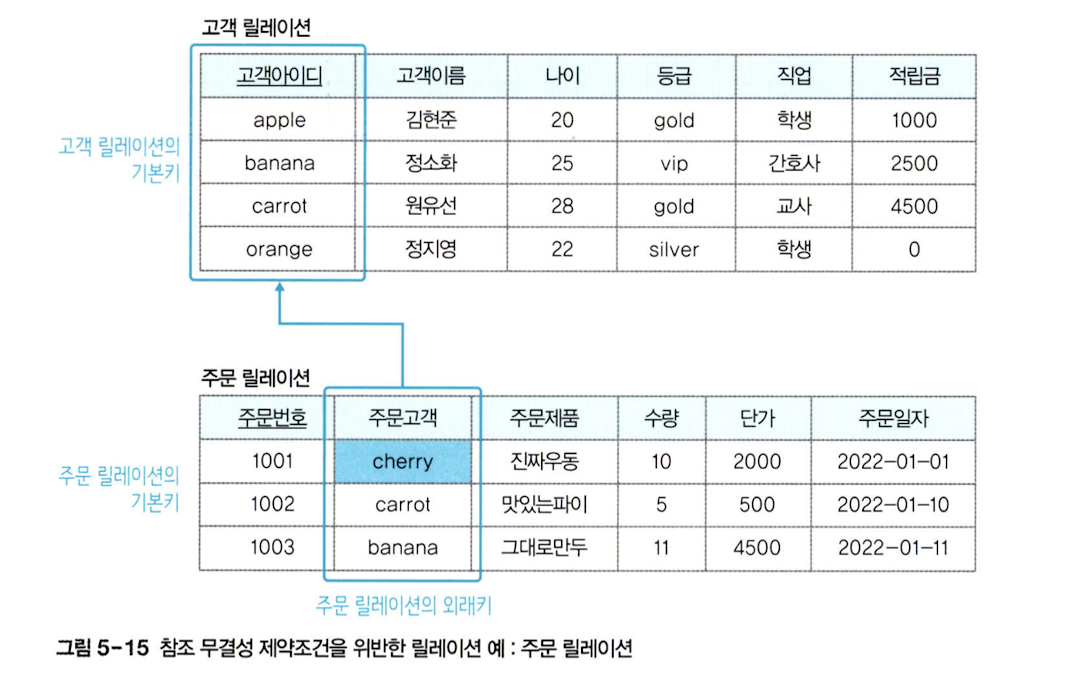
위 사진에서, 주문 릴레이션의 주문고객 속성은 고객 릴레이션의 기본키인 고객아이디 속성을 참조하는 외래키다. 참조 무결성 제약조건을 만족하려면 주문고객 속성 값이 현재 고객 릴레이션에 존재하는

Chpater 6

01. 관계 데이터 연산의 개념

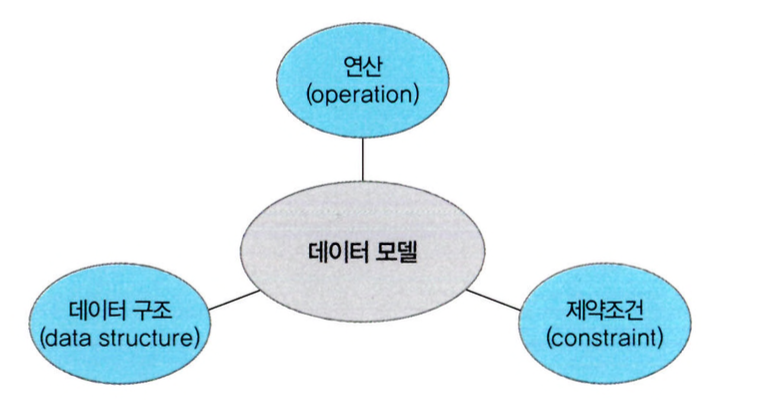
관계 데이터 모델에서 연산은 원하는 데이터를 얻기 위해 릴레이션에 필요한 처리 요구를 수행하는 것으로, 데이터베이스 시스템의 구성 요소 중 데이터 언어의 역할을 합니다.

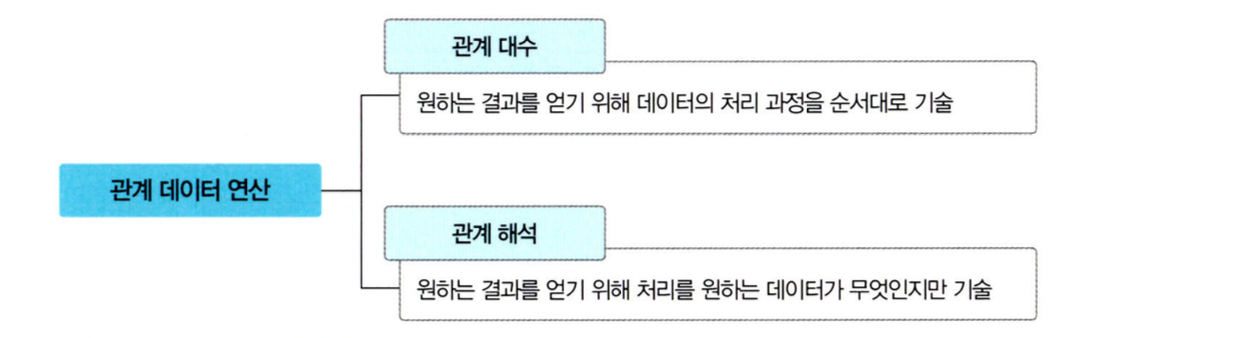
관계 대수는 원하는 결과를 얻기 위해 데이터의 처리 과정을 순서대로 기술하는 절차 언어
관계 해석은 원하는 결과를 얻기 위해 처리를 원하는 데이터가 무엇인지만 기술하는 비절차 언어

관계 대수와 관계 해석을 공부해야 하는 이유

• 새로운 데이터 언어가 제안되면 해당 데이터 언어의 유용성을 검증해야 하는데 검증의 기준 역할을 하는 것이 관계 대수와 관계 해석이다.

02. 관계 대수

1. 관계 대수의 개념과 연산자

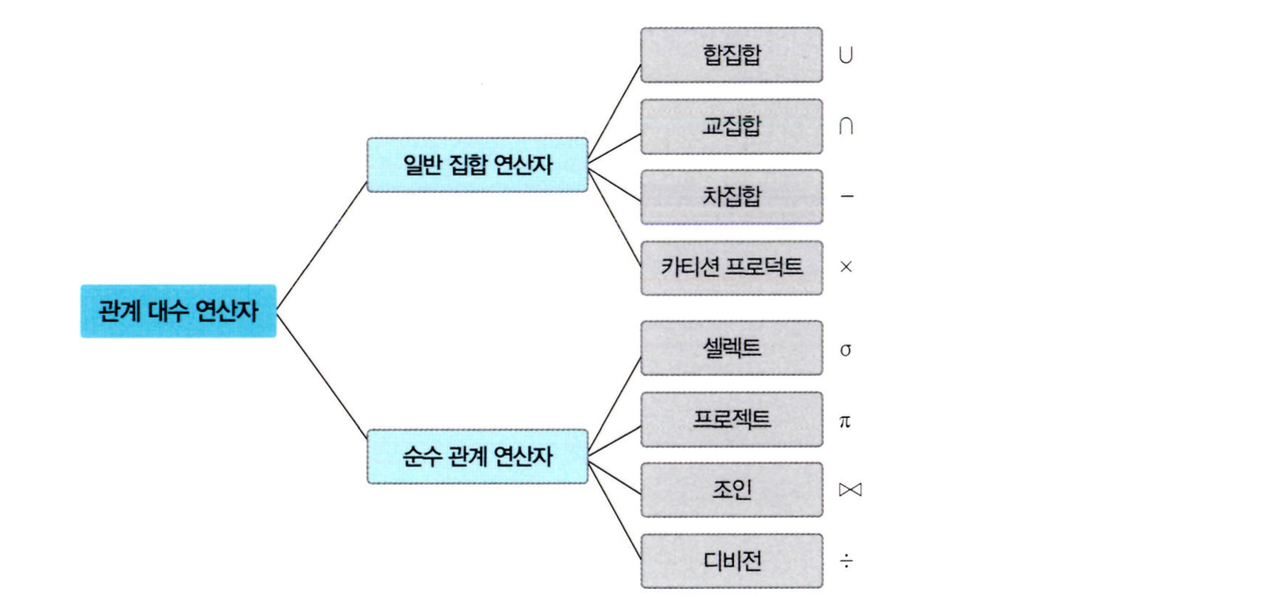
관계 대수는 원하는 결과를 얻기 위해 릴레이션을 처리하는 과정을 순서대로 기술하는 언어로, 연산자들의 집합으로도 정의할 수 있습니다. 즉 관계 대수는 릴레이션을 연산합니다.

릴레이션을 연산하면 결과로 릴레이션을 얻는데, 이러한 관계 대수의 특성을 폐쇄 특성이라고 합니다.

관계 대수에 속하는 대표적인 연산자 8개는 특성에 따라 일반 집합 연산자와 순수 관계 연산자로 분류할 수 있습니다.

일반 집합 연산자
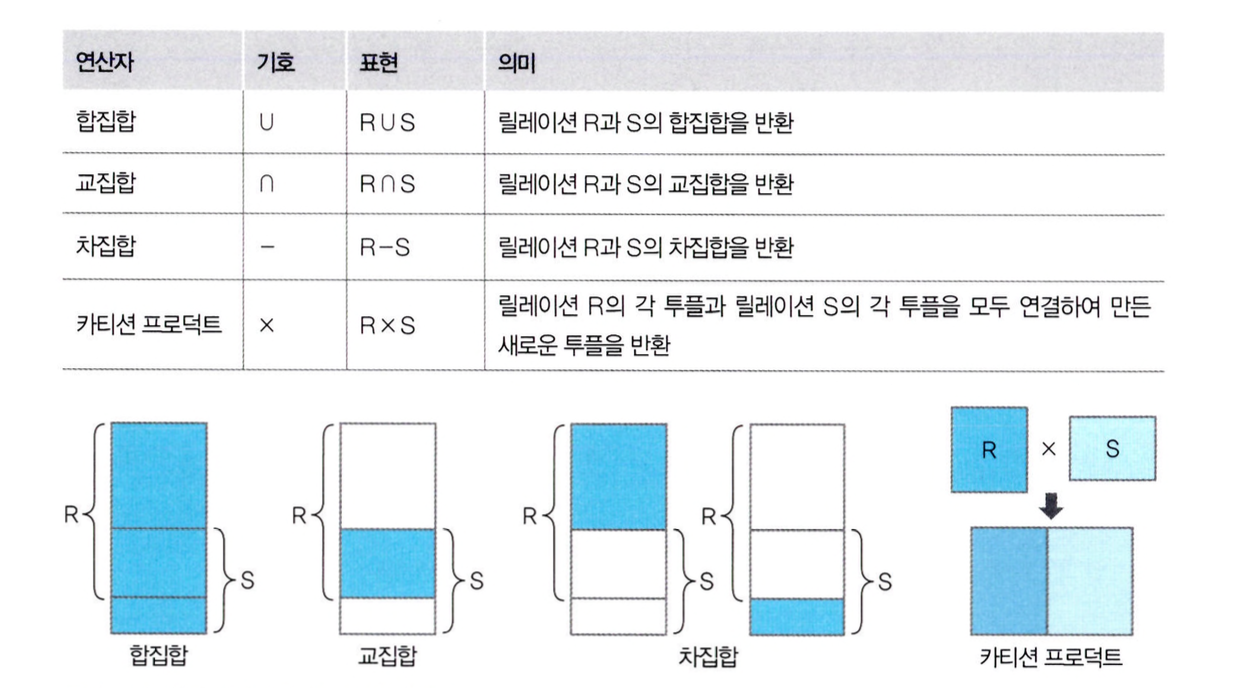
일반 집합 연산자는 릴레이션이 투플의 집합이라는 개념을 이용하는데, 이는 수학의 집합 관련 연산자를 차용한 것입니다.
일반 집합 연산자에 속하는 연산자의 종류와 기능은 다음과 같습니다.

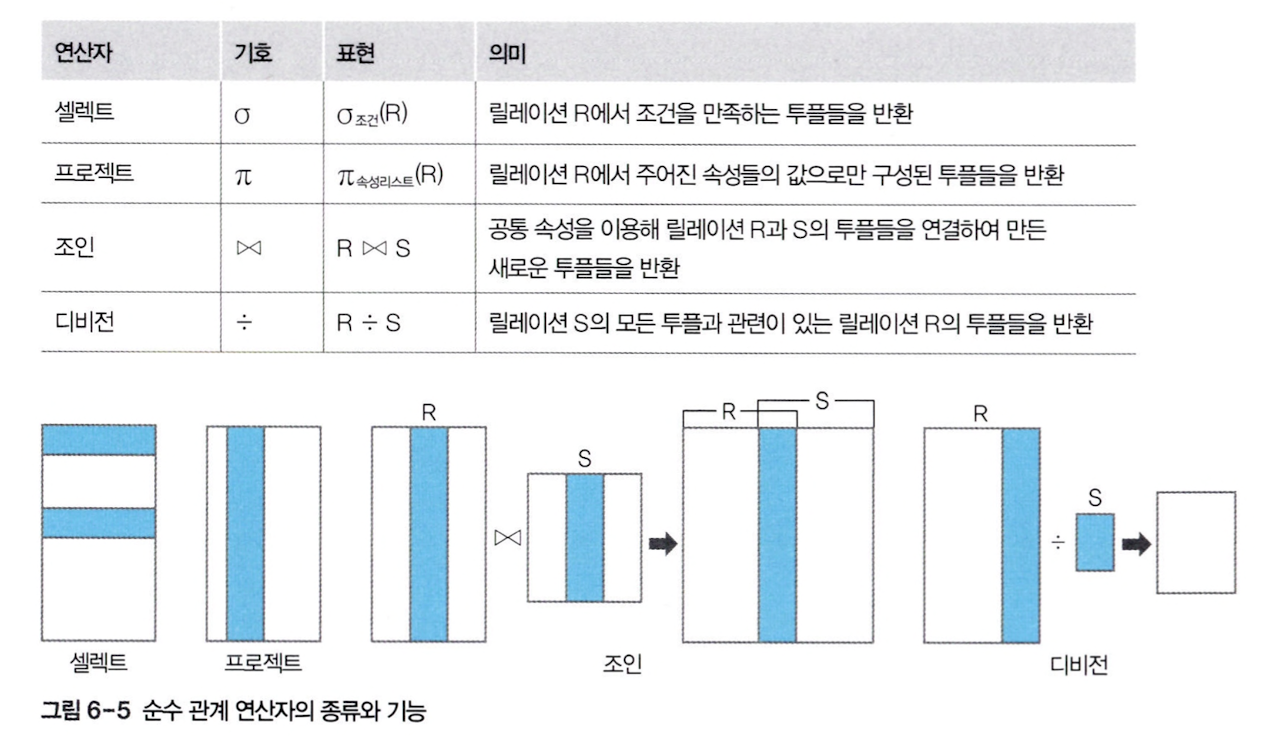
순수 관계 연산자
순수 관계 연산자는 릴레이션의 구조와 특성을 이용하는 것으로 관계 데이터 모델에서 새로 제시된 연산자입니다.
순수 관계 연산자에 속하는 연산자의 종류와 기능은 다음과 같습니다.