최소 신장 트리 (Minimum Spannig Tree)
spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리.
MST는 간선에 가중치를 고려하여 최소 비용의 스패닝 트리를 선택하는 것,
- Spanning Tree는 그래프의 최소 연결 부분 그래프이다 (그래프에서 일부 간선을 선택해서 만든 트리
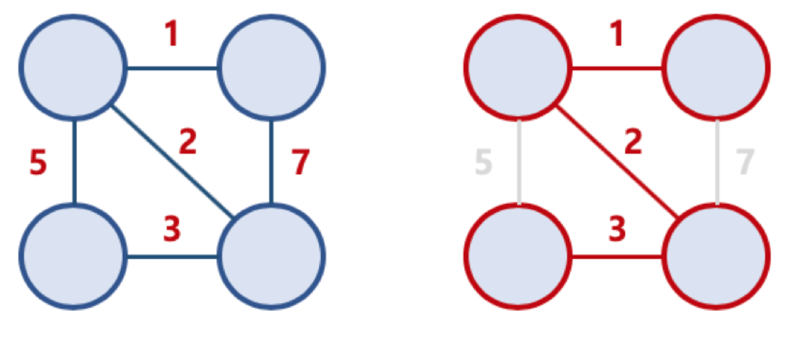
조건
- 본래의 그래프의 모든 노드를 포함
- 간선의 가중치의 합이 최소여야 한다
- 모든 노드가 서로 연결 되어있다
- 트리의 속성을 만족 (사이클이 존재하지 않는다)
크루스칼 알고리즘 (Kruskal Algorithm)
- 최소 비용 신장 트리를 찾는 알고리즘
- 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘
- 최소 스패닝 트리를 찾음으로써 간선의 가중치의 합이 최솟값이 되도록 하는 알고리즘
- 스패닝 트리 : 그래프에서 일부 간선을 선택해서 만든 트리
- 최소 스패닝 트리 : 스패닝 트리 중에 선택한 간선의 가중치의 합이 최소인 트리
동작 원리
- 모든 간선들의 가중치를 오름차 순으로 정렬
- 가중치가 가장 작은 간선을 선택
- 위에서 선택한 간선이 연결하려는 2개의 노드가 서로 연결되지 않은 상태라면, 2개의 노드를 서로 연결한다.
- 이 과정을 반복
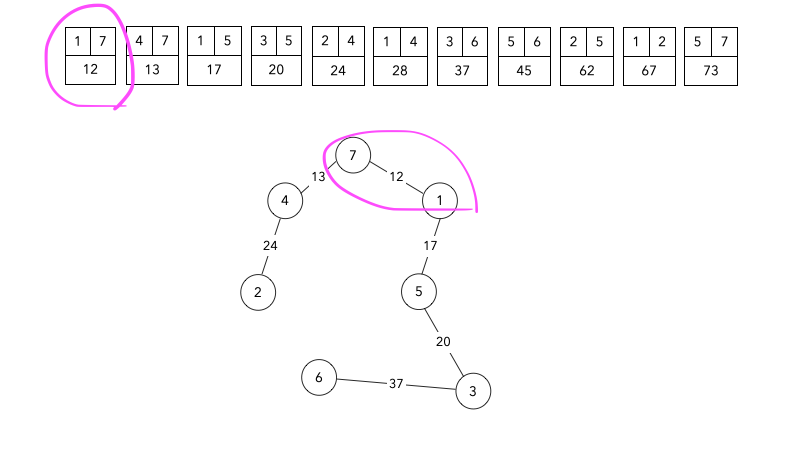
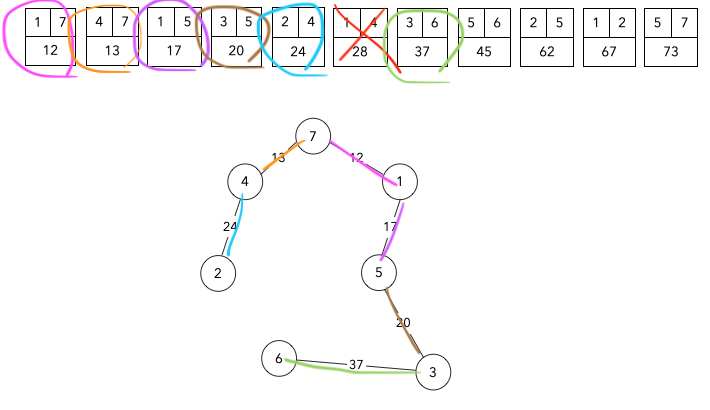
모든 간선들의 가중치를 오름차 순으로 정렬

가중치가 가장 작은 간선을 순서대로 선택하고 연결
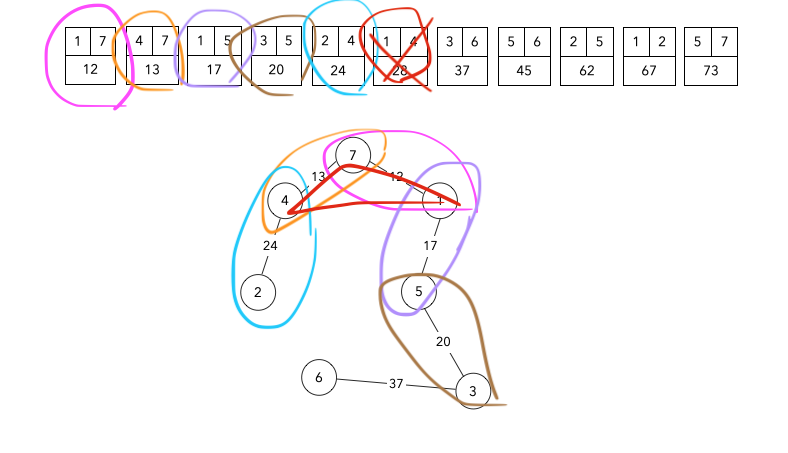
2번 과정에서 사이클이 발생했을 시엔 포함을 하지 않는다
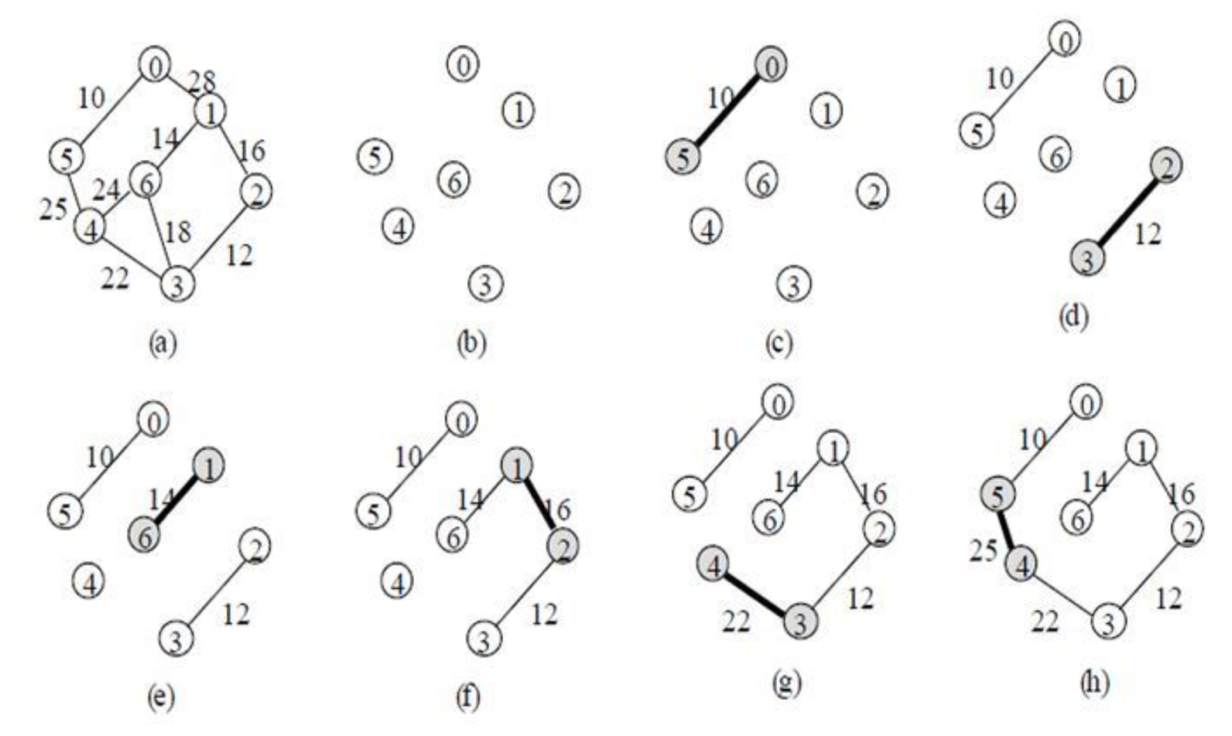
프림 알고리즘 (Prim Algorithm)
- 시작 정점을 기준으로 가장 작은 간선과 연결된 정점을 선택하며 신장 트리를 확장 시키는 알고리즘
- 정점 선택을 기반으로 하는 알고리즘
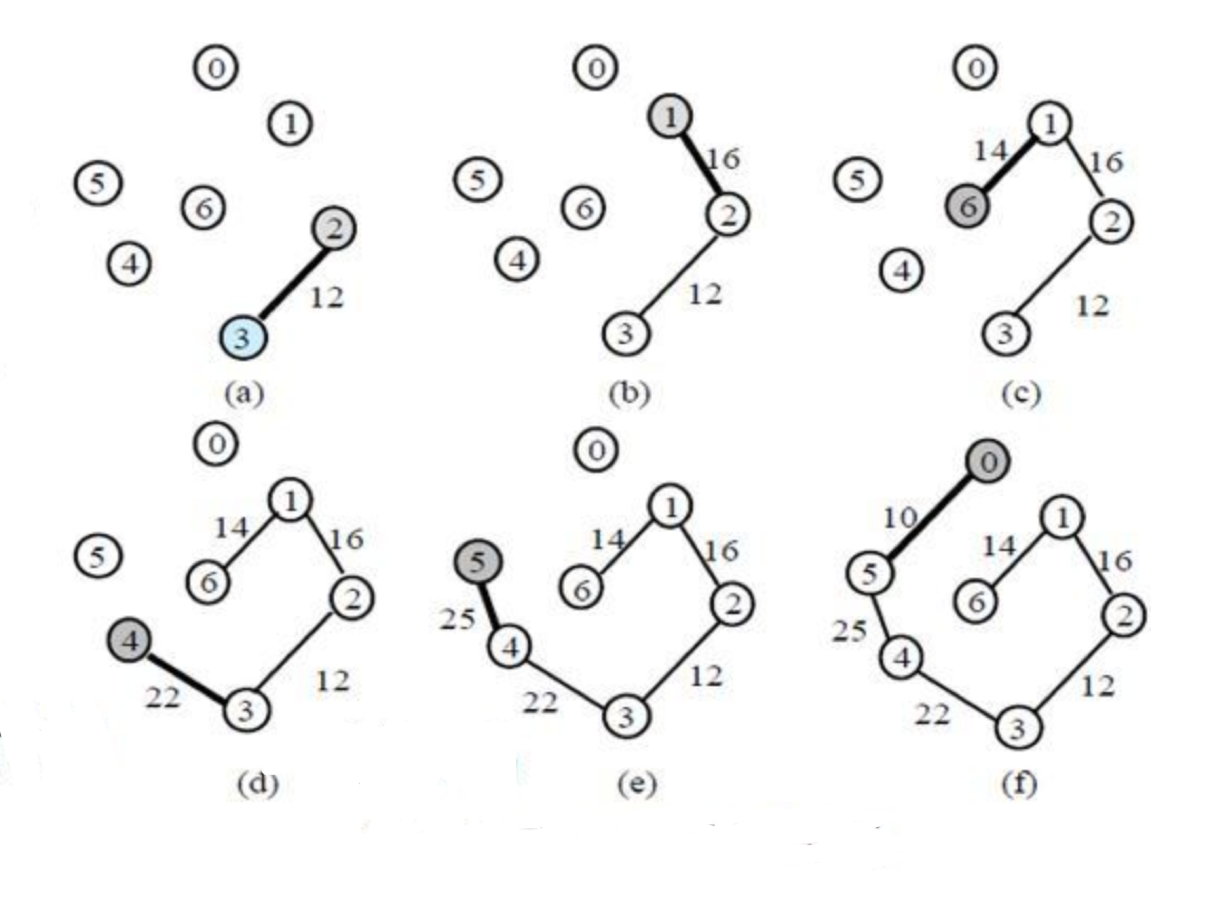
동작 원리
- 임의의 간선을 선택
- 선택한 간선의 정점으로부터 가장 낮은 가중치를 갖는 정점을 선택
- 모든 정점이 선택될 때까지 반복
크루스칼 VS 프림
- 프림은 정점 위주의 알고리즘, 크루스칼은 간선 위주의 알고리즘
- 프림은 시작점을 정하고, 시작점에서 가까운 정점을 선택하면서 트리르 구성 하므로 그 과정에서 사이클을 이루지 않지만 크루스칼은 시작점을 따로 정하지 않고 최소 비용의 간선을 차례로 대입 하면서 트리를 구성하기 때문에 사이클이 이루어지는 항상 확인 해야한다.
- 프림의 경우 최소 거리의 정점을 찾는 부분에서 자료구조의 성능에 영향을 받는다.
- 크루스칼은 간선을 기준으로 정렬하는 과정이 오래 걸린다.
- 간선의 개수가 작은 경우에는 크루스칼, 간선의 개수가 많은 경우에는 프림.
자세한 시간 복잡도와 구현 코드는 아래 링크
https://godls036.tistory.com/26
간선의 개수 小: 크루스칼 多: 프림
감사합니다.