문제설명
숫자 배열 nums가 주어 졌을때 가장 큰 원소들의 합을 가진 부분배열의 합을 return 하시요(최소한 하나의 숫자는 있어야 합니다).
예시
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
풀이
모든 부분배열 경우의 수를 찾아 비교하는 Brute Force로 풀 수도 있지만 O(n^2), O(n^3)의 아주 비효율 적인 코드가 됩니다.
좀 찾아보니 이 문제는 카데인(Kadane) 알고리즘을 사용해서 풀어야 하는 유명한 문제였습니다. 먼저 제가 이해한데로 최대한 카데인 알고리즘을 설명해보겠습니다.
먼저 보통 Brute Force의 방법은 앞에서 부터 하나씩 모든 경우의 수를 찾아 갑니다.
Brute Force로 경우의 수를 찾는 방법
카데인 알고리즘은 뒤에서 부터 경우의 수를 찾는다는 가정에서 시작합니다.
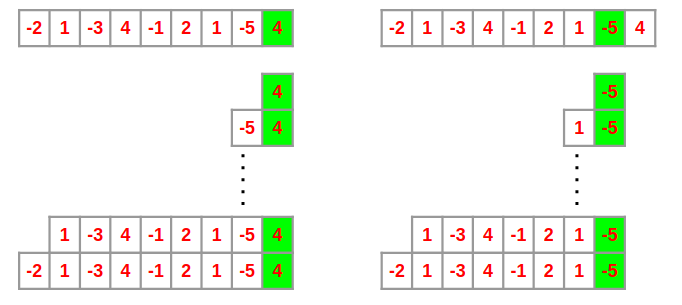뒤에서 부터 경우의 수를 찾아가는 방법
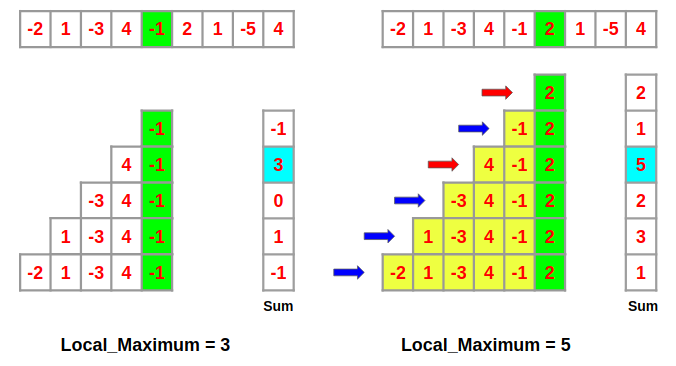
원리를 설명하기 위해 배열(Array)의 4번 째와 5번 째 index의 원소로 끝나는 부분 배열(Array[4] ,Array[5])를 예로 들어 보겠습니다.
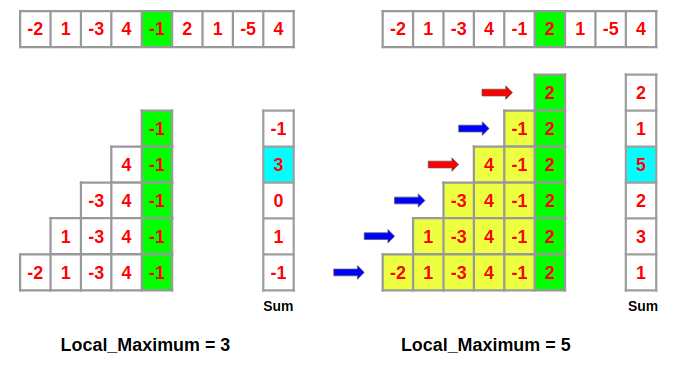
위에를 그림을 보시면, 4번 째 배열까지의 모든 부분 배열 중 최댓값은 [4,-1] 배열의 3입니다. 그리고 보면 Array[5]로 끝나는 부분배열은, Array[4]로 끝나는 부분배열에(노란 부분) Array[5]의 원소 값을(초록색) 더 한 것이란 걸 알 수 있습니다.
그렇다면 Array[4]까지의 부분배열 중 최댓값을 갖는 부분배열(localMaximum이라 하겠습니다)을 알고 있다면, localMaximum[5]을 찾기 위해서 모든 경우의 수를 알 필요가 없게 됩니다. 이미 Array[4]의 부분배열에서 가장 큰 합을 가진 [4,-1] 배열을 찾았고 Array[5]에서는 전 부분 배열에 Array[5]의 원소값(2)만 더해주면 되니까 [4,-1]보다 작은 합을 가진 나머지 부분 변수들은 신경 쓸 필요가 없습니다.
즉 localMaximum[5]를 찾기 위해서는, localMaximum[4]에 Array[5]가 더해진 [4,-1, 2]와 Array[5]의 값([2]) 두 개만 비교해주면 됩니다(그림 상에서 빨간 화살표).
식으로 표현한 Kadane's Algorithm
index i의 local_maximum은, A[i]와 A[i]와 그 전 index i-1의 local_maximum의 합 중 더 큰 수 입니다.
코드
var maxSubArray = function(nums) {
for(let i = 1; i < nums.length; i++){
nums[i] = Math.max(nums[i], nums[i]+nums[i-1])
}
return Math.max(...nums)
}느낌점
카데인 알고리즘을 알고 있냐 없냐에 따라 난이도가 크게 달라지는 문제였습니다. 처음 찾아봤을 때 글로 읽고 이해하기 힘들었어서 최대한 쉽게 설명해보려고 했는데 괜히 더 복잡해진거 같기도 하네요;; 나중에 다시 읽어보고 좀 더 다듬어 보겠습니다.
[참고]"Kadane’s Algorithm — (Dynamic Programming) — How and Why does it Work?"
