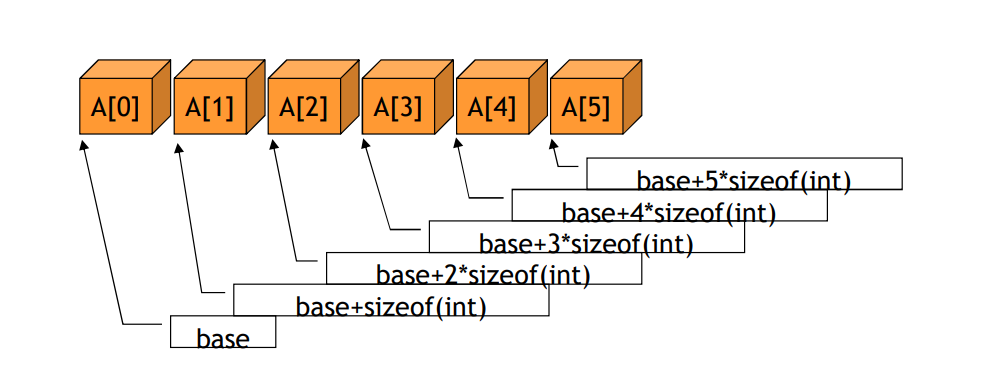
🎈 Array

: systematic arrangement of multiple variable with same data type sequentially.

🧷 Array VS Structure

• Array : group data of the same type.
• Structure : group data of different types.
  thus, comparing between structure variables can't be implemented
  ex ) person p1 > person p2 (x)

📥 Self-Referential Structrue

: Structrue that has one or more pointers to itself in the field. Is often used in linked lists or trees.

typedef struct ListNode {
char data[10];
struct ListNode *link;
} ListNode;

📰 Structrue Array

#define MAX_STUDENTS 200
#define MAX_NAME 100

typedef struct {
int month;
int date;
} BirthdayType;

typedef struct {
char name[MAX_NAME];
BirthdayType birthday; // another structure 
} StudentType;

StudentType students[MAX_STUDENTS];

void main()
{
strcpy(students[0].name, “HongGilDong”);
students[0].birthday.month = 10; //Approach Hierarchically 
students[0].birthday.date = 28;
}

📐Applications of Arrays: Polynomials

: Let's see how Addition operation in polynomial works using structure.

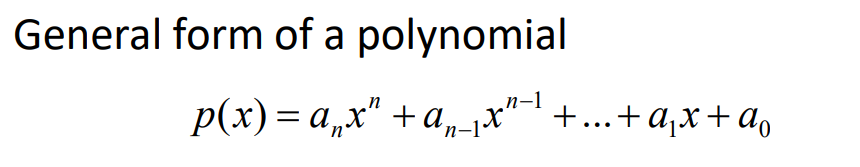
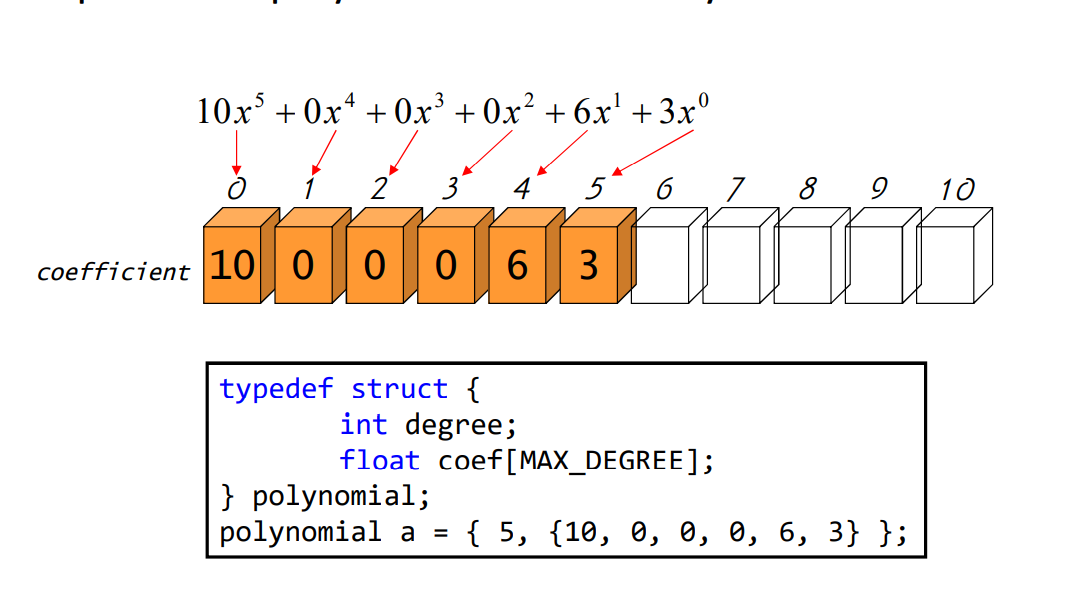
1. Polynomial Representation in Arrays (1)

: Store all terms of a polynomial in an array. one polynomial in single structure.

– Pros: Simplified polynomial operations
– Cons: It causes wasteful space, when most of the coefficients
are zero.

#include <iostream>
#define MAX(a,b) (a>b ? a:b)
#define MAX_DEGREE 101

using namespace std;

typedef struct {

	int degree; //차수
	float coef[MAX_DEGREE]; // 항들의 계수 


}polynomial;

polynomial add(polynomial A, polynomial B) {


	polynomial C;
	int Apos = 0, Bpos = 0, Cpos = 0;
	int degree_A = A.degree;
	int degree_B = B.degree;
	C.degree = MAX(A.degree, B.degree); //C의 차수 = A,B중 최고차항

	while (Apos <= A.degree && Bpos <= B.degree) {


		if (degree_A > degree_B) // A의 차수가 더 크다면
		{
			C.coef[Cpos++] = A.coef[Apos++]; //A항을 C항에 옮긴다.
			degree_A--;

		}
		else if (degree_A > degree_B) //차수가 같다면
		{

			C.coef[Cpos++] = A.coef[Apos++] + B.coef[Bpos++];
			degree_A--;
			degree_B--;
		}
		else // B의 차수가 더 크다면
		{
			C.coef[Cpos++] = B.coef[Bpos++]; //A항을 C항에 옮긴다.
			degree_B--;

		}
	}
		return C;
}

int main() {


	polynomial A = { 5,{3,6,0,0,0,10} };
	polynomial B = {4,{7,0,5,0,1} };
	polynomial C = add(A, B);

}

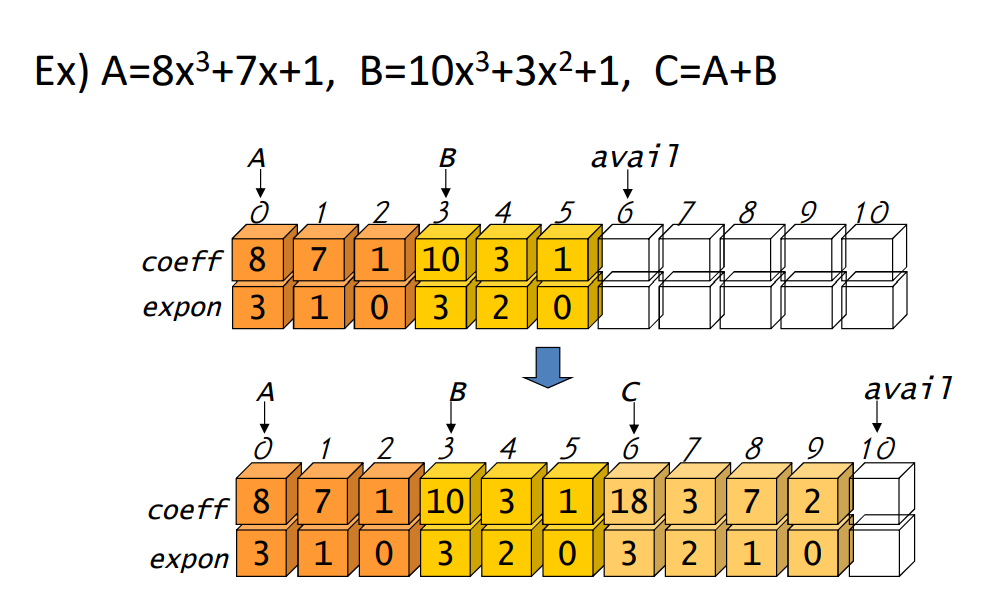
2. Polynomial Representation in Arrays (2)

: Store only non-zero terms of a polynomial in an array.
multiple polynomial in single array.

• Pros: Efficient use of memory space
• Cons: Polynomial operations are complex

#include <iostream>
#define MAX_TERMS 101

using namespace std;


struct {

	float coef;
	int expon;

}terms[MAX_TERMS] = { {8,3},{7,1},{1,0},{10,3},{3,2},{1,0} };

//위 문장의 의미? 구조체 배열을 만든다? 

int avail = 6; //결과를 넣을 인덱스 배열의 시작점

//compare two integers

char compare(int a, int b) {


	if (a > b) return '>';
	else if (a == b) return '=';
	else return '<';

}

void attach(float coef, int expon) { //새로운 항을 새로운 다항식 C (결과)에 추가한다.

	if (avail > MAX_TERMS) {

		fprintf(stderr, "too many terms\n");
		exit(1);
	}
	//avail이 오른쪽으로 한칸씩 움직이면서 새로운 항을 추가함.
	terms[avail].coef = coef; //계수넣기
	terms[avail++].expon = expon;  //지수 넣고 인덱스 뒤로 이동
}

void add(int As, int Ae, int Bs, int Be, int* Cs, int* Ce) {

	float tempcoef; //덧셈 저장용
	*Cs = avail;


	while (As <= Ae && Bs <= Be) {

		switch (compare(terms[As].expon, terms[Bs].expon))

		{

		case '>': //A항 차수 > B항 차수
			attach(terms[As].coef, terms[As].expon);

			As++; // A를 다음 항으로
			break;

		case '=':  //A항 차수 = B항 차수

			tempcoef = terms[As].coef + terms[Bs].coef; //A항 계수 + B항계수 합친것 

			if (tempcoef) //만일 더했을때 계수가 0이라면 새로운 다항식 C에 추가할필요가 없음. (없는항)
				attach(tempcoef, terms[As].expon); //2번째인자는 terms[Bs].expon 여도 상관X 어짜피 차수 같으니..

			As++; Bs++;
			break;

		case '<': //A항 차수 < B항 차수
			attach(terms[Bs].coef, terms[Bs].expon);
			
			Bs++; // B를 다음 항으로
			break;



		}
	}

		//Q. 항들이 어떻게 남아있을 수 있냐? 
        //A. while문 조건이 As <= Ae && Bs <= Be 이기때문.
		 
		//A에 남아있는 항들을 복사 붙여넣기
		for (; As <= Ae; As++) {

			attach(terms[As].coef, terms[As].expon);
			
		}
		for (; Bs <= Be; Bs++) {

			attach(terms[Bs].coef, terms[Bs].expon);
			
		}
		
	

	*Ce = avail - 1; //avail은 현재 비어있는 공간을 가리키고 있으므로 -1을 해주어야 C가 끝나는 지점의 index가 됨.


}
int main() {


	int Cs, Ce; //결과 다항식의 시작 & 끝 인덱스를 담을 변수
	add(0, 2, 3, 5, &Cs, &Ce); //A다항식의 시작과 끝, B다항식의 시작과 끝.
	//주소를 넘겨주어야 실질적으로 값을 변경할 수 있음.

	for (int i = Cs; i <= Ce; i++) {

		cout << terms[i].coef<<' ';
	}
	
}

📓 Sparse Matrix

: Matrix where most terms are zero

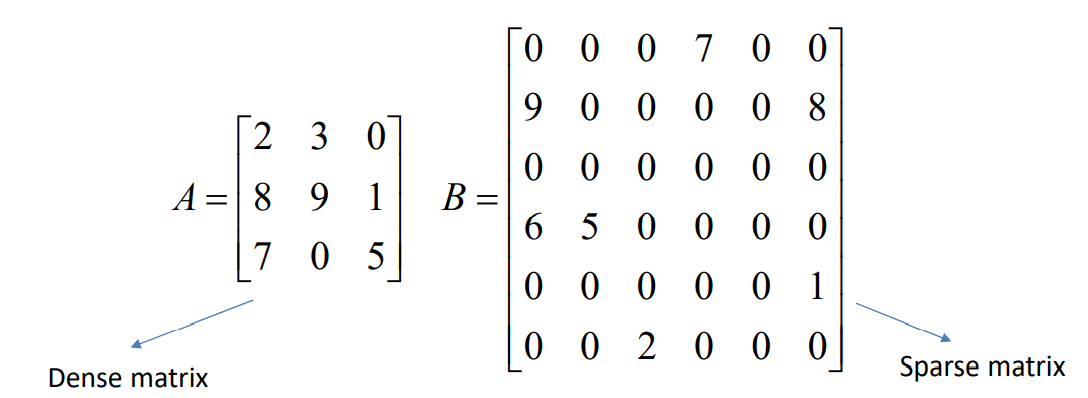
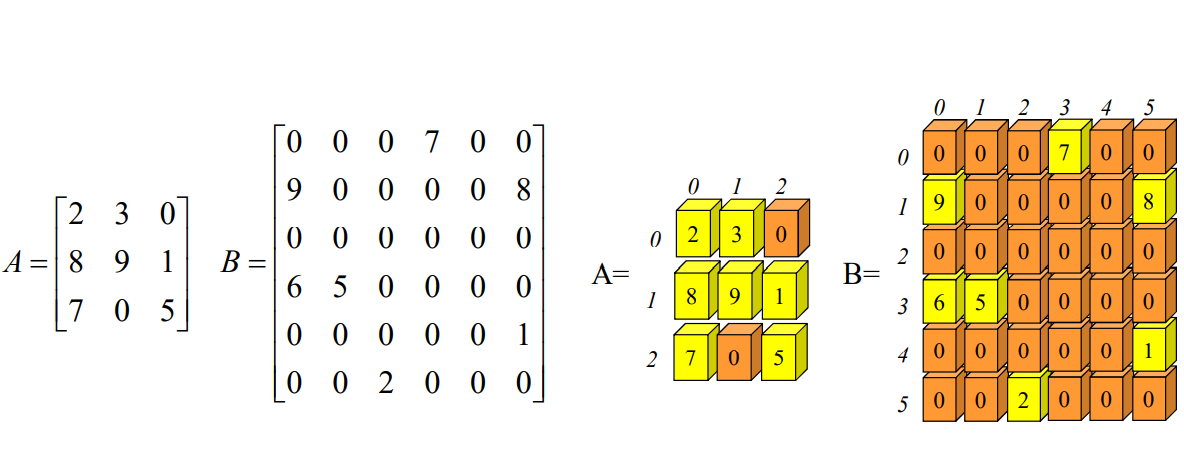
1. Sparse Matrix Representation (1)

: store all elements in a 2D array

• Pros: Matrix operations can be implemented simply.
• Cons: Memory is wasted when most terms are zero

#include <stdio.h>
#define ROWS 3
#define COLS 3
// Addition
void sparse_matrix_add1(int A[ROWS][COLS], int B[ROWS][COLS], int C[ROWS][COLS]) // C=A+B
{
int r,c;
for(r=0;r<ROWS;r++)
for(c=0;c<COLS;c++)
C[r][c] = A[r][c] + B[r][c];
}
main()
{
int array1[ROWS][COLS] = { { 2,3,0 },{ 8,9,1 },{ 7,0,5 } };
int array2[ROWS][COLS] = { { 1,0,0 },{ 1,0,0 },{ 1,0,0 } };
int array3[ROWS][COLS];
sparse_matrix_add1(array1,array2,array3);
}

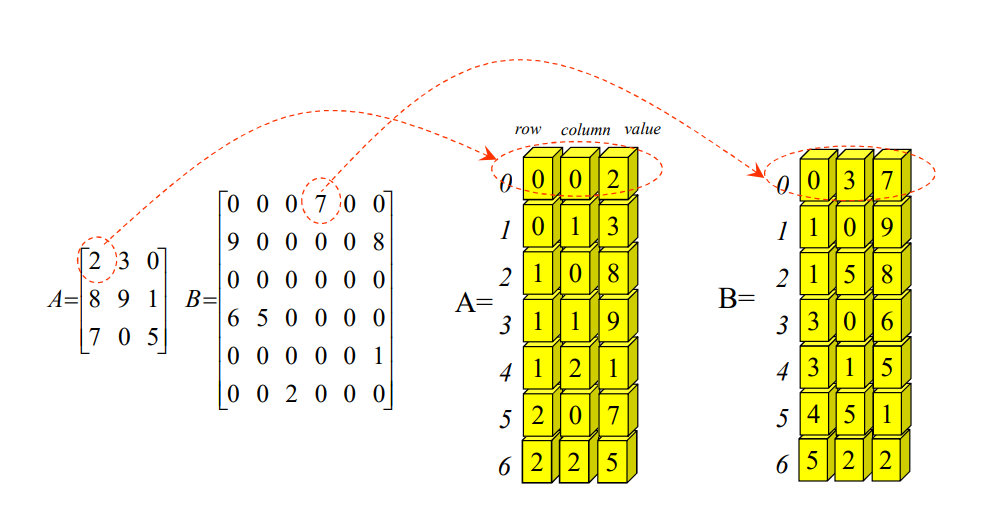
2. Sparse Matrix Representation (2)

: store only non-zero elements

• Pros: Memory is saved for sparse matrices
• Cons: Complex implementation of matrix operations

#include <iostream>

#define ROWS 3
#define COLS 3
#define MAX_TERMS 10

using namespace std;


typedef struct {

	int row; //행
	int col; //열
	int value; //값
}element;

typedef struct SparseMatrix{

	element data[MAX_TERMS];
	int rows; //매트릭스 행 크기
	int cols; //매트릭스 열 크기
	int terms; //element의 수 -> max랑 같은거 아닌가

}SparseMatirx;

SparseMatrix  sparse_matrix_add2(SparseMatrix a, SparseMatrix b) {


	SparseMatirx c;

	int ca = 0, cb = 0, cc = 0; //배열 a,b,c 의 data의 인덱스를 각각 가리키는 변수. 

	// 배열 a와 배열 b가 같은 사이즈인지 확인한다.
	if (a.rows != b.rows || a.cols != a.rows) {

		fprintf(stderr, "size가 같지 않아 덧셈 불가능");
		exit(1);
	}

	//배열 덧셈 결과인 C의 행,열 크기 세팅
	c.rows = a.rows; //a==b이므로 b여도 상관 X
	c.cols = a.cols;
	c.terms = 0;

	//rows cols가 일치하면 c에 추가한다.

	while (ca < a.terms && cb << b.terms) {

		// 각각의 item의 index를 계산한다. ->어떤항을 먼저 삽입할지 알기위함.

		int inda = a.data[ca].row * a.cols + a.data[ca].col; //배열c에 a가 들어갈 index.

		//만약에 ca가 가리키는 값이 2행 3열이라면 c에서 2*3+3 번째에 위치하게됨.
		int indb = b.data[ca].row * b.cols + b.data[ca].col;  //배열c에 b가 들어갈 index.

		if (inda < indb) { //a가 더 먼저나온다면 (c배열에는 윗줄부터 차례로 넣어야하므로 큰 값이 나중에 채워짐)

			c.data[cc++] = a.data[ca++];
		}

		// a==b라면

		else if (inda == indb) {

			if (a.data->value + b.data->value != 0) {

				//c.data =a.data+b.data 가 불가능하기 때문에 각각 고려해서 대입해주어야함.

				c.data[cc].row = a.data[ca].row; //b여도 상관 X
				c.data[cc].col = a.data[ca].col; //b여도 상관 X
				c.data[cc].value = a.data[ca++].value + b.data[cb++].value; //c는 a값과 b값을 더한값
			}
			else
				ca++; cb++; //더했을때 항이 0이므로 그냥 패스하고 다음항.

		} //b가 더 먼저 나온다면
		else
			c.data[cc++] = b.data[cb++];

	}

}


int main() {

	SparseMatirx m1 = { {{ 1,1,5 },{ 2,2,9 }}, 3,3,2 };
	SparseMatrix m2 = { {{ 0,0,5 },{ 2,2,9 }}, 3,3,2 };
	SparseMatrix m3;
	m3 = sparse_matrix_add2(m1, m2);

}

🔖 Array and Pointer

Array name = pointer

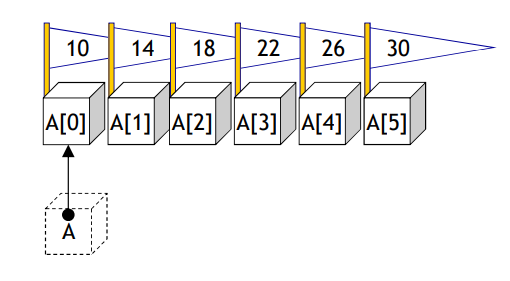
: The compiler replaces the array name with the first address in
the array.

📦 Structure Pointer

• -> : used to access elements of a structure from pointer
  

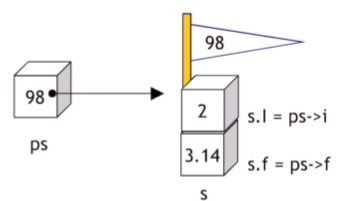
ps -> i , s.i , *(ps).i
: same notation of access member of structure

🎭Pointer of Pointer

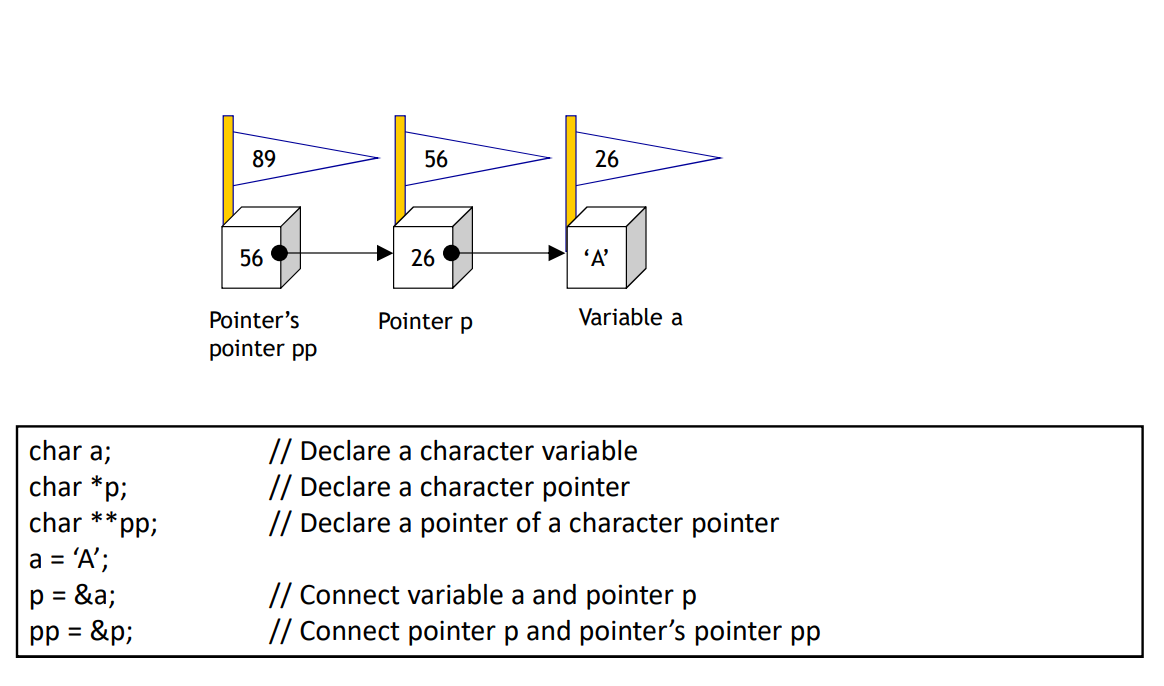
🧷* and & operation can be canceled out.

Q. What **pp imply?
A. pp = &p -> *pp = p -> *pp = &a (p=&a) -> **pp = a

🔧Pointer Operation

pointer reflects how many byte Data type occupy

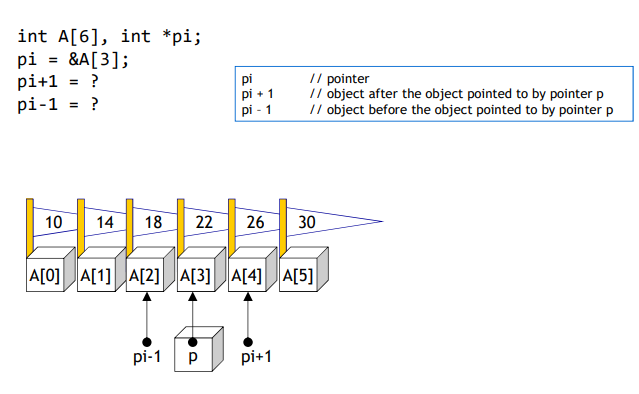
• pi-1 : address of previous element

• pi+1 : address of next element

• NULL Pointer : pointing to nothing
  ex) int *pi =NULL;

size of data type

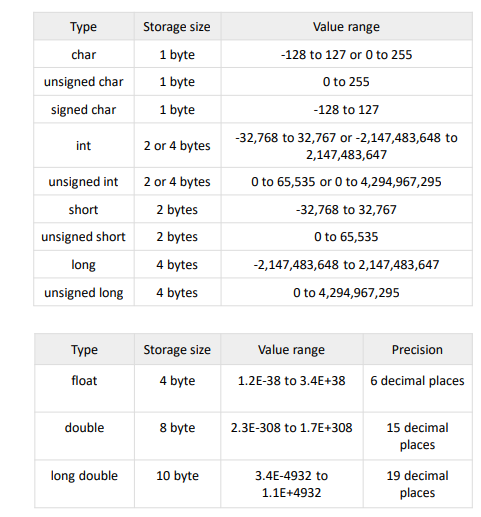
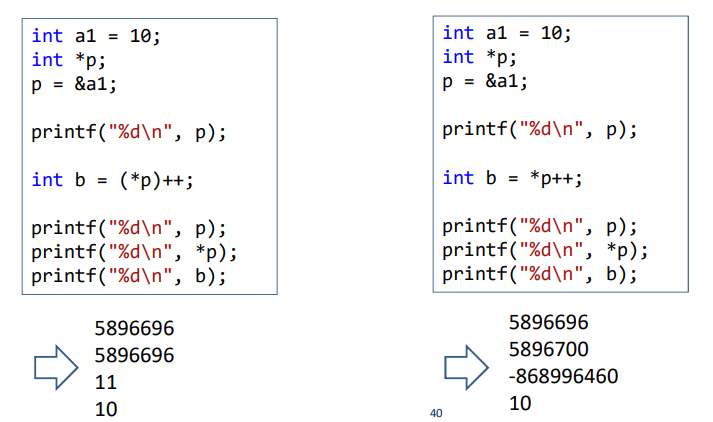
Q. (*p)++ VS *(p++)
A. the prioirity of operation is quite diffent.
++ 's priority is higher than *

(p)++ -> 1. apply 2. ++ apply
(p++) -> 1. ++ apply 2. apply

🗄Dynamic Memory Allocation

: To allocate memory during program execution. It enables very efficient use of memory

• malloc (size) : allocate the memory block of size byte and return the start address of allocated memory
  
• free (ptr) : deallocate
• sizeof (var) : return the size of variables or type (in bytes)

main()
{
int *pi;
pi = (int *)malloc(sizeof(int)); // Dynamic Memory Allocation
...
... // Use dynamic memory
...
free(pi); // Release dynamic memory
}

🧱Memory Allocation of 2D Array

allocation method 1

void main()
{
int row = 3;
int col = 3;
int **m2 = (int **)malloc(sizeof(int *)*row);
for (int i = 0; i<row; i++)
m2[i] = (int *)malloc(sizeof(int)*col);
int count = 0;
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
m2[i][j] = ++count; //i행 j번째 요소의 값 초기화
printf_s("%d\n", m2[i][j]);
}
}
}

allocation method 2

int count = 0;
for (int i = 0; i < row; i++)
{
int *tmp = *(m2 + i); //tmp는 i행의 시작주소를 담게됨
for (int j = 0; j < col; j++)
{
tmp[j] = ++count; //tmp[j]가 의미하는것은  i행 j번째 요소
printf_s("%d\n", tmp[j]);
}
}

Q. why tmp[j] means elements at i row and j th col?

A. firstly, p[n] means move n from p's adderess and apply * operation
ex) p[1] == *(p+1)
then tmp = *(m2+i) --- apply [j] ---> tmp[j] = *(*(m2 + i) + j)

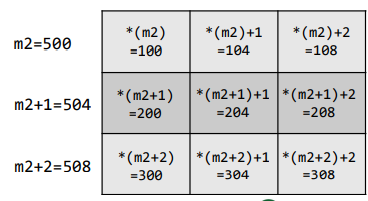
Deallocation

:not only m2, but also m2[0]

if (m2 != NULL)
{
free(m2[0]); //행들의 주소가 연속적으로 담겨져있는 시작 포인터 
free(m2); // 첫번째 행의 시작주소를 가리키는 포인터 
m2 = NULL;
}