10844: 쉬운계단수
아이디어
- (A+B+C+D)%E = A%E + B%E + C%E + D%E
즉, 다 더한다음에 E로 나누면 overflow나니까 계산결과가 나올때마다
E로 나눠준다 - 숫자를 하나씩 만들어간다고 생각하자. 가장중요한 수는 맨뒷자리수다. 맨뒷자리수가 무엇이냐에 따라 다음에 올 수가 결정된다.
- 예시를 통해 규칙을 찾는것이 중요하다.
- 예시를 통해 규칙을 찾으려했지만 찾기 힘들었다. 잘나누는 것도 필요하다
우리가 규칙을 잘 찾기 위해서는 잘 나누어 놓는것이 중요하다.
맨뒷자리수가 가장 중요하고, 이에따라 다음수가 결정된다면
맨뒷자리수가 무엇이냐에 따라 숫자들을 다 나눠보자
코드
import java.io.*;
import java.lang.reflect.Array;
import java.nio.Buffer;
import java.util.ArrayList;
import java.util.Arrays;
public class Main{
//dp[n][k]: 맨뒷자리수가 k이면서 자릿수는 n개인 수들의 개수를 의미
//dp[1][2]: 은 숫자 2를 의미한다. 자릿수는 1개이면서 맨뒷수는 k즉 2다
static long dp[][];
//입력받는 수 n을 의미한다.
static int n;
//문제를 재귀적으로 해결하는 함수를 만들었다.
//기록이 되기때문에 매우짧은시간내에 해결이 가능하다
public static long solve(int n, int k){
//아래 조건이 없으면 stackoverflow난다
//k에 대한 조건은 없어도된다 아래의 코드에서 알아서 잡아주기때문
//k가 너무커질려하는순간 = 9 에서 알아서 컷해줌
//k가 너무작아지려고하는순간 = 0에서 알아서 컷해줌
//그래서 우리는 n을 계속 감소시키다보면 n==1인곳에 도달할거고
//그곳은 기본값으로 지정해줬기때문에 무조건그 값을 return하고 재귀를끝내도록해준다
if(n == 1) return dp[n][k];
//dp에 값이 저장되어있는경우 그 값을 return해준다 대신 나눠서 리턴해준다
// 모두 더한다음에 나누는거나 각값을 나눈다음에 더하는것이나 같기떄문에 이같은연산이 가능하다
if(n==1&&k==9||dp[n][k]!=0) return dp[n][k]% 1000000000;
//k==0인 경우에는 규칙에서 보인 특성에 따라 자릿수를 낮추고 k번쨰의 개수를 리턴한다
//자릿수가하나작고, 9로끝나는 숫자들로 dp[n][k]에 해당하는 숫자를만들수있기대문이다
if(k==0) {
dp[n][k] = solve(n-1, 9);
return dp[n][k];
}
//1인 경우에 규칙을 살펴보면 자신보다 하나큰수로 자기자신을 만들수있다.
//이들은 모두 자기보다 작은수에 대해서 값을가져와서 채우는데
//n==1인 기본값이 채워져있어서 재귀적으로 이런작업이가능한것이다
else if(k==1){
dp[n][k] = solve(n-1, k+1);
return dp[n][k];
}
//9인 경우도 예외적으로 k+1, k-1로 처리할수없기때문에 아래와같이 직접숫자를넣어주었다
else if(k==9) {
dp[n][k] = solve(n-1, 8)+ solve(n-1, 0) ;
return dp[n][k];
}
//그외의 숫자들은 모두 아래와같은 규칙으로 적용이 가능하다
//값을 기록해야하기때문에 기록하는과정을빼먹지말자
else{
dp[n][k] = solve(n-1, k+1) + solve(n-1, k-1);
return dp[n][k];
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
dp = new long[n+1][10];
//초기화하는 작업
for(int i=0;i<10;i++){
dp[1][i] = 1;
}
//자릿수가 1개이면서 0으로끝나는 숫자는 없다
//0은 해당되지않는다
dp[1][0] = 0;
//solve(n,1)만 하면 숫자 1에 대해서만 조사하기때문에..
//모든숫자를 채워서 재귀탐색을하기위해선 0~9까지를 조사해야한다
for(int i=0;i<=9;i++){
solve(n,i);
}
//조사를 마친 후 배열에 저장된 값들을 모두 더해준다
long sum = 0l;
for(int i=0;i<10;i++){
sum += dp[n][i];
}
//너무커질수도있으니 나눠준다
bw.write(sum % 1000000000 +"");
bw.flush();
bw.close();
}
}
11726: 2xn 타일링
아이디어
- N번쨰의 요소가 이전값들과 어떤관계가있는지를 생각해보았다.
N번째요소는 N-2번쨰요소에 세로로긴 막대기 하나붙인결과 + N-1요소에 가로로 긴 막대기 하나를 붙인 결과에 해당했다
11057: 오르막수
아이디어
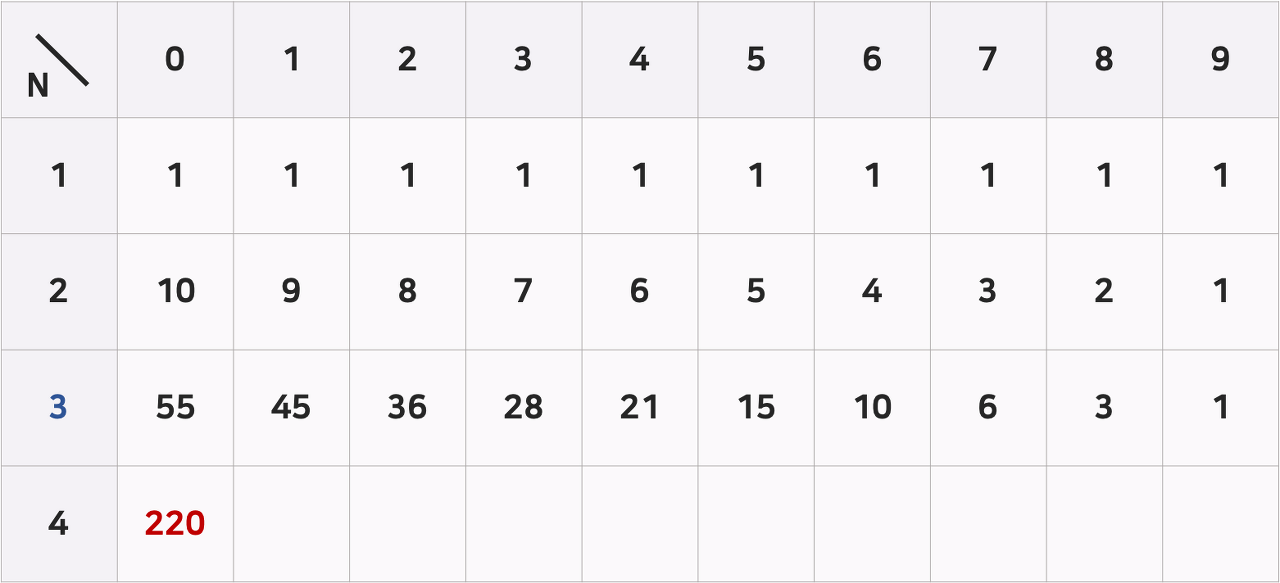
n은 자릿수
0~9는 0~9로끝나는 수
즉, 220은 4자리수이면서 0으로끝나는 수의 갯수를 의미한다
220은 n=4-1인 n=3의 모든값을 더한 결과와 같다.
n=2쪽이 좀더 이해하기 쉽다
(n=2,k=0)인 수는
(n=1,k=0)~(n=1,k=9)의 합과 같다.
import java.io.*;
import java.lang.reflect.Array;
import java.nio.Buffer;
import java.util.ArrayList;
import java.util.Arrays;
public class Main{
//
//
static long arr[][];
public static long solve(int n, int k){
//계속 n-1만하다보면 n이 음수가 돼버린다. 그에 대응하는 배열값은 없다
//멈춰주어야한다. 종료조건이 있어야한다
if(n<=0) return 0l;
//memorization을 통해 여기서 함수의 재귀를 멈춰준다
if(arr[n][k]!=0) return arr[n][k];
long sum = 0l;
//i는 k부터 9까지여야한다
//그러니까 가장 마지막수가 i라면 그 뒤의 수는 무조건 i보다 크거나 같아야한다는얘기다
for(int i=k;i<=9;i++){
long x = solve(n-1,i);
sum= (sum + x) % 10007;
}
arr[n][k] = sum;
//다 더한뒤에 나누는거나 중간중간 더하는과정에서 매번나누는거나 똑같다
return arr[n][k] % 10007;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
//n+1인이유는 n=0인칸은 안쓸것이기때문이고
//10으로 써준이유는 0부터9까지수를 써줄것이기때문이다
arr = new long[n+1][10];
//가장 아랫단에 있을 수들을 초기화해주어야한다
//이값이 없으면 함수가 stackoverflow날것이다.
//함수가 더이상 호출못하게 끝맺음해주는부분이있어야한다
for(int i=0;i<=9;i++){
arr[1][i] = 1;
}
long sum =0l;
//solve를할때마다 n번쨰자릿수에서 i번째로 끝나는 수의 갯수가 출력된다
//해당 갯수를 모두 더하면 n번째자릿수의 오르막수를 구할 수 있다
for(int i=0;i<=9;i++){
sum = (sum + solve(n,i)) % 10007;
}
bw.write(sum%10007+"");
bw.flush();
bw.close();
}
}
2193: 이친수
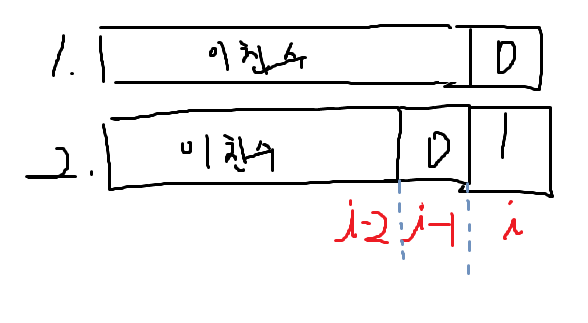
이친수가 되기위해선
이친수 + 0 이거나
이친수 + 01 이여야한다
n자리 이친수를 구하기위해서
n-2자리이친수 + 0 과
-1자리 이친수 + 01을 가져오면된다
즉, dp[n]=dp[n-2]+dp[n-1]이 성립한다.
11053: 가장긴증가하는수열
public static void solve(){
dp[0] = 1;
//원소 하나하나를 보고. 이 원소를 이전원소들과 비교하여 얼마나 큰지를 따져봐야한다
for(int i=1;i<arr.length;i++){
//일단 최소길이가 1이기때문에 1로 세팅해주었다
dp[i] = 1;
//i번째 이전원소에 대해. 첫번째원소부터 시작하여 만약에 i보다 큰값이여서 증가하는 수열에 포함될수있다면 포함시켜줘야한다
for(int k=0;k<i;k++){
//dp는 같을수도있다. 맨처음에 1로 초기화하기때문에 처음엔 같을수도있다. 하지만 일단 arr값이 크다면 업데이트해주어야하기때문에
//dp[i]>=dp[k]에 등호를 넣었다
//값은 내가 더 큰데 dp의 값, 즉 이전원소들이 만들어놓은 수열이 더 긴경우
//기존것에 합세한다
if(dp[i]<= dp[k] && arr[i] > arr[k]){
//기존것에 합세하는거기때문에 기존값+1을해준다
dp[i] = dp[k]+1;
}
}
}11055: 가장 큰 증가 부분 수열
public static int solve(){
//이런 이런 식의 부분 증가수열은 기준점을 잡은 후 기준점 이전까지의 수들과 비교하여 자신이 큰 경우만 dp 배열을 갱신해주면된다
// 증가 부분 수열 중에서 합이 가장 큰 것을 나타내는 변수 result
//수열의 합은 0보다는 클테니까 0을 초기화한다
int result =0;
//입력받은 수열의 갯수만큼 for문을 돌린다
for(int i=0;i<arr.length;i++){
//가장 합이 큰녀석에 대해서 이어나갈것이다
int max = 0;
//기준원소이전원소들을 모두탐색하는데, 나보다 값이 작은놈을 선택
//그리고 이원소의 sum의 값을 가져와서 max를 갱신한다
//max에는 가장 큰 합이 들어있을것이다.
for(int k=0;k<i;k++){
if(arr[k]<arr[i]){
max = Math.max(sum[k],max);
}
}
//for문을 다 돌고 나면 max에는 이전까지의 원소들중 가장 큰 값이 들어있을테고,
//sum에는 기존합+현재값을 갱신해준다
sum[i] = max+ arr[i];
//그리고 result는 sum의 값들중 최댓값을 return할것이기때문에
//겸사겸사 계산한다
result = Math.max(sum[i], result);
}
return result;
}1932: 정수삼각형
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Objects;
import java.util.StringTokenizer;
import static java.util.Objects.*;
public class Main{
static int arr[][];
static int sum[][];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
//삼각형에 대한 정보를 담을 arr배열
arr = new int[n][n];
//삼각형가장꼭대기에서 아래로부터 합을 저장할 sum배열
sum = new int[n][n];
//입력받는 부분
for(int i=0;i<n;i++){
String input[] = br.readLine().split(" ");
//1개,2개,3개....n개 이렇게 입력받을 것임
for(int k=0;k<=i;k++){
arr[i][k] = Integer.parseInt(input[k]);
}
}
//삼각형의 꼭대기는 (0,0)을의미하며, 합또한 자기자신이다.
sum[0][0] = arr[0][0];
//최솟값이 0이니 0을 다 합해도 -1보단 크다. 가장작은값보다 작아야하니 -1으로 선정하였다
int result = -1;
//이중포문이어도 입력 크기가 작아서 가능
//i=0부터시작하지않아도되는이유는. 삼각형의꼭대기를 코드윗부분에서 설정해주었기때문이다.
for(int i=1;i<n;i++){
//1개, 2개, 3개, n개.. 씩 즉, 삼각형의 한줄씩 보기위한 for문
for(int k=0;k<=i;k++){
//k==0이라는것은 삼각형의 가장왼쪽부분에 있다는사실, 이렇게되면 sum[i-1][k-1]에대한값을 구할 수 없어서
//아래와 같이 예외처리한다
if(k==0){
int tempMax = sum[i-1][k];
sum[i][k] = tempMax + arr[i][k];
}
//일반적인 경우라면 자기 윗부분 + 자기 왼쪽부분 중 최댓값을 선정해서 그 값과 자기자신을 더해주면된다.
//삼각형의 가장오른쪽에있는부분은 어차피 자기 윗부분이 0이 나올것이기때문에 알아서 무시되는것을 확인할 수 있다
else {
int tempMax = Math.max(sum[i - 1][k], sum[i - 1][k - 1]);
sum[i][k] = tempMax + arr[i][k];
}
}
}
//결과는 삼각형의 가장 마지막줄에서 가장 큰값을 선택하면된다
for(int k=0;k<n;k++){
result = Math.max(result, sum[n-1][k]);
}
bw.write(result+"");
bw.flush();
bw.close();
}
}9465: 스티커
오해했던 점
스티커가 모두 찢어진다는게아니라 하나씩만 떼어지는 건 줄 알았다.
풀이1
- 일단 Node라는 class를 따로만들어서 위치와 value를 저장한다
그리고 Node를 정렬한다
가장큰값부터 꺼내서 그 인근값들은 못가게 false로 바꾼다
근데 이런식으로하면
0 80 100 80
0 0 80 0
이런 배열이 있을때 최댓값을 찾지 못한다.
무조건 가장큰 값부터 찾는다고 해서 최대를 보장해주지 않는다.
풀이2
스티커가 모두 찢어지는것이라면. 내가 i번째 배열요소를 봤을때 그 요소는 이전 요소들과 어떤 관계가 있을지 생각한다.
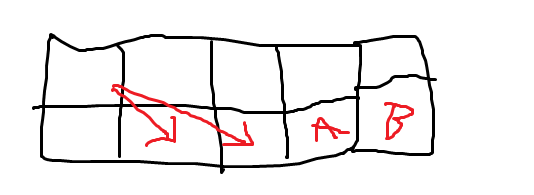
화살표에 해당하는 두 지점에만 갈 수 있다.
A와 B는 갈 수 없는것이 아니지만, 문제조건상 최댓값을 찾고, 요소들엔 모두 양수가있을것이기때문에 그 이전 요소들을 무조건 들러주는것이 최댓값을 찾을 수 있게 해준다.=
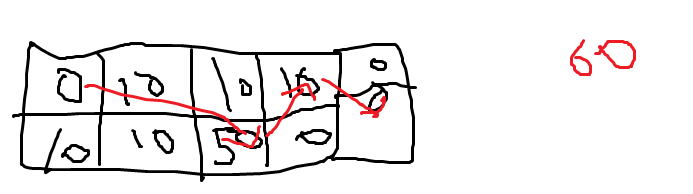
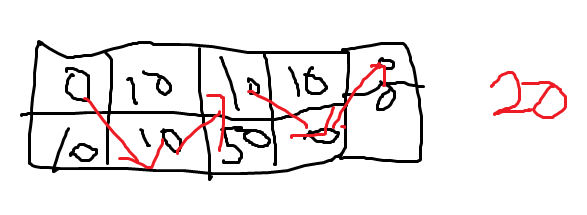
- 화살표가 다음아래칸을 가리키는지 다다음아래칸을 가리키는지에 따라 최댓값이 변한다. 무조건 다음아래칸을 가리킨다고 해서 더 많은 값을 가져올 수 있는게 아니라. 보여드린 예시처럼 세번째 아래에 있는 50의 경우, 매우 큰 숫자일 경우에 다다음 아래칸이 더 합이 클 수 있다.
왜 4번째 아래의 0과 5번째 아래의 0은 선택하면 안되는것일까?
- 두번째아래10을 선택해도, 네번째 0을 선택할 수 있다.
- 세번째아래 50을 선택하면 5번째 아래의 0을 선택할 수 있다.
그러니까 결국 두번쨰아래와 세번째 아래만 고려하면 나머지를 다 고려할 수 있게 되는 것이다.
코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.Objects;
import java.util.StringTokenizer;
import static java.util.Objects.*;
public class Main{
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
for(int i=0;i<n;i++){
int x = Integer.parseInt(br.readLine());
//두줄, x개의 칸의 이차원 배열 선언
//이 배열안에는 초기 입력값이 들어갈것임
int arr[][] = new int[2][x];
//최댓값을 구해나갈 배열변수
//arr의 값을 보면서 dp[0][?]과 dp[1][?]의 값을 채워나갈것이다
int dp[][] = new int[2][x];
//입력받는 부분, 두줄을 입력받을 것이다
for(int k=0;k<2;k++){
String input[] = br.readLine().split(" ");
//x번만큼 띄어서 입력받기
for(int j=0;j<x;j++){
arr[k][j] = Integer.parseInt(input[j]);
}
}
//초깃값 세팅 해주어야 아래 for문이 예외없이 잘돌아감
dp[0][0] = arr[0][0];
dp[1][0] = arr[1][0];
for(int j=1;j<x;j++){
//이거for문 밖으로 빼면 배열 밖 범위 초과 < error뜸
if(j==1){
//일단 첫번째dp의 경우 j-2의 값이 없기때문에 다음과 같이 하나의 값으로만 더해준다
//즉, 자기값 + 자기 이전 대각선 값으로 dp를 세팅해준다
dp[1][1] = arr[0][0] + arr[1][1];
dp[0][1] = arr[1][0] + arr[0][1];
}
else{
//이전대각선 vs 이이전 대각선 중 더 큰 값 + 자기자신
//dp[0][?]과 dp[1][?]을 동시에 세팅해주어야한다
dp[0][j] = Math.max(dp[1][j-1], dp[1][j-2]) + arr[0][j];
dp[1][j] = Math.max(dp[0][j-1],dp[0][j-2]) + arr[1][j];
}
}
//계속 더해나가다보면 배열의 가장 끝 두 값 중 가장 큰 값으로 출력해주면된다
//가장 마지막은 어쨋든 가장 마지막끝에서 발생될것이기 때문
bw.write(Math.max(dp[0][x-1], dp[1][x-1])+"\n");
}
bw.flush();
bw.close();
}
}2156: 포도주 시식
처음에는 xooxoo와 ooxoox의경우의수만 세주면된다고 생각했다.
일단 한번선택할때 두개를 선택하는게 무조건 이득이라고생각했기떄문이다
oxooxoo이런선택지가 있다는것을 몰랐따.
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.OptionalInt;
public class Main{
static int n;
static int wine[];
static int dp[];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
wine = new int[n+1];
dp = new int[n+1];
for(int i=0;i<n;i++){
wine[i] = Integer.parseInt(br.readLine());
}
//예외처리
if(n==1){
bw.write(wine[0]+"\n");
bw.flush();
bw.close();
return;
}
if(n==2){
bw.write( wine[1]+wine[0]+"\n");
bw.flush();
bw.close();
return;
}
if(n==3){
bw.write(Math.max(Math.max(wine[0]+wine[1],wine[0]+wine[2]), wine[1]+wine[2])+"\n");
bw.flush();
bw.close();
return;
}
//초깃값 세팅
dp[0] = wine[0];
dp[1] = wine[1]+wine[0];
//2번쨰까지오는데 최댓값은
//0,1 이렇게 와인을 먹거나
//1,2 이렇게 와인 먹거나
//0,2 이렇게 와인먹는 세가지 경우 중 하나이다
dp[2] = Math.max(Math.max(wine[0]+wine[1],wine[0]+wine[2]), wine[1]+wine[2]);
//i-3이있기때문에 위에 예외처리 과정을 해주었따
for(int i=3;i<n;i++){
//oox : dp[i-1]
//xoo: dp[i-3]+wine[i-1]+wine[i]
//oxo: dp[i-2]+wine[i]
//왜 dp에 넣는 인덱스가 x의 위치-1인가요?
//x기준왼쪽이 최댓값을 알아서 선택했다고 가정하는것이다.
//만약에 모든경우엥서 dp[i-3]을 해주고 o인경우는 wine[]을 더해주고 이렇게 된다면
//앞에서 oo을 선택하고 뒤에서도 oo을 선택하여 3개이상이 될 가능성이있다.
//그래서 x이전의 처리는 알아서 3개가 안되도록 앞에게 맡기고
//그 이후의 처리만 하는것이다
int max = Math.max(Math.max(dp[i-2]+wine[i], dp[i-3]+wine[i-1]+wine[i]), dp[i-1]);
dp[i] = max;
}
bw.write(dp[n-1]+"\n");
bw.flush();
bw.close();
}
}11052: 카드구매하기
public class Main{
static int n;
static int card[];
static int dp[];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
card = new int[n+1];
dp = new int[n+1];
String input[] = br.readLine().split(" ");
//card에 대한 정보를 입력받는다
//idx를 card갯수로 조회하고 싶어서 n+1만큼 선언
for(int i=1;i<=n;i++){
card[i] = Integer.parseInt(input[i-1]);
}
//기본 전략은 다음과 같다
//구하려는것: 개수 x를 가지는 카드가격의 최댓값
//개수가 예를들어 x라면. 1~x까지의 여러 조합을 통해
//1 x-1
//2 x-2 이런조합을 통해 합이 x인 것들중 최댓값을 dp에 저장한다
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i] = Math.max(dp[i-j] + card[j], dp[i]);
}
}
bw.write(dp[n]+"\n");
bw.flush();
bw.close();
}
}15486 퇴사2
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.lang.reflect.Array;
import java.util.ArrayList;
import java.util.OptionalInt;
public class Main{
static int n;
static int[] dp;
public static void solve(){
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
//dp[x]: x일 이전까지 일을 했다고 가정했을떄 x날에 받을 돈의 최댓값
//n일까지 일할테니까 dp[n+1]의값을 구하면된다
//문제를 쪼개서 생각해보면
//x일이전까지일을했고 + 지금 이일을했을때 그떄가서 받을 돈, 이일을 하지 않는다고 가정했을때 내가 받을 최댓값
//중에 최댃값을 매번 갱신해준다
//그리고 dp의 값은 이전의 최댓값을 그대로 끌고와야 계속 누적이 된다
dp = new int[n+2];
for(int i=1;i<=n;i++){
String input[] = br.readLine().split(" ");
int period = Integer.parseInt(input[0]);
int pay = Integer.parseInt(input[1]);
//값을 끌고오는 것
dp[i] = Math.max(dp[i-1], dp[i]);
//대상의 원래값(지난 idx에서 누군가가 더큰값으로 업데이트했을수도있으니) vs i번째날기준 i-1까지 일을했고, i번째날에 받을돈 + 이번에 내가 일을 하며 받을돈,
int target = period+i;
if(target<n+2) dp[target] = Math.max(dp[target], dp[i] + pay);
}
dp[n+1] = Math.max(dp[n], dp[n+1]);
bw.write(dp[n+1]+"");
bw.flush();
bw.close();
}
}11058 크리보드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.lang.reflect.Array;
import java.util.ArrayList;
import java.util.OptionalInt;
public class Main{
static int n;
static long dp[];
static long solve(int idx){
if(idx<=0) return 0;
if(dp[idx]!=0) return dp[idx];
//큰수부터 시작하기때문에 dp[idx-1]+1을넣으면 0에다 +1을 한 값을 넣게된다
//일단 여기서 부터 재귀호출을 하여서 값을 구해놓은 다음에 for문을 돌려야한다
//1. A만 추가하는경우
dp[idx] = solve(idx-1)+1;
//idx의 위치보다 3칸 왼쪽에 있는애부터 계속왼쪽으로 한칸씩 간다
//그래서 왼쪽으로 한칸 갈때마다 곱하는 수를 늘려준다
//아래의 식은 예제를 만들어서 식을 세웠다.
//2. Ctrl(복붙)하는 경우: 이경우는 세세하게 나눠보면
//세종류의 버튼을 누르는것과 세종류의 버튼을 이미 눌렀다면 버튼 하나만 눌러도되는경우가있다
//근데 이경우를 아래 for문으로 합칠 수 있다.
//solve(i):i번 버튼을 눌렀을때의 A의 최댓값
//세종류의 버튼을 이미 눌렀다고 가정하고 시작을해야한다. 그래야 두번쨰 복붙의 경우도 진행이 가능하니까
//그래서 3을빼주는것이다. 이미 버튼이 눌려졌다고 가정한다
//그리고 A의 갯수는 하나 줄이고 곱하는수(곱하는버튼)은 늘리면서 가장 큰 조합을 찾아서
//dp에 저장한다
for(int i=idx-3;i>=1;i--){
dp[idx] = Math.max(solve(i) * (idx-i-1), dp[idx]);
}
return dp[idx];
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
//예외처리
if(n==1) {
bw.write("1\n");
bw.flush();
bw.close();
return;
}
if(n==2){
bw.write("2\n");
bw.flush();
bw.close();
return;
}
dp = new long[n+1];
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
bw.write(solve(n)+"\n");
bw.flush();
bw.close();
}
}12865: 평범한 배낭
시도1
-
아래의 직사각형이 물건이라고 가정할떄 다음과 같이 하면 최댓값을 구할 수 있을것이라고 생각했다. 근데 아래와 같이 로직을 짜게 되면
다음 예시에서 잘못된 답을 도출할 것이다.
3 5
3 4
2 1
1 100
104를 도출해야하는데 101을 도출한다.
그이유는 일단 감당할수있는 weight보다 합이 작으면 추가해주기때문이다.
추가해주는 값이 최대의 value를 보장한다고 말할수있는가?
없다. -

import com.sun.jdi.request.BreakpointRequest;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.lang.reflect.Array;
import java.util.ArrayList;
import java.util.OptionalInt;
public class Main{
static int n;
static long dp[];
//가방안에 넣는 물건을 정의한 class
public static class Thing{
//무게
int weight;
//가치
int value;
Thing(int w, int v){
this.weight = w;
this.value = v;
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String input[] = br.readLine().split(" ");
int n = Integer.parseInt(input[0]);
int weight = Integer.parseInt(input[1]);
Thing[] things = new Thing[n];
for(int i=0;i<n;i++){
String input2[] = br.readLine().split(" ");
int w = Integer.parseInt(input2[0]);
int v = Integer.parseInt(input2[1]);
things[i] = new Thing(w,v);
}
ArrayList<Integer> resultList = new ArrayList();
for(int i=0;i<n;i++){
//매 반복마다 최대value를 구합니다
int max =0;
int currentWeight = 0;
//weight보다 작으면 가장왼쪽부터 더해나갑니다
if(things[i].weight +currentWeight <= weight) {
max = Math.max(things[i].value, max);
currentWeight += things[i].weight;
}
//가장왼쪽부터 weight보다 합계 무게가 적으면 더해나갑니다
for(int j=i+1;j<n;j++){
if(things[j].weight + currentWeight <= weight){
max += things[j].value;
currentWeight += things[j].weight;
}
}
resultList.add(max);
}
int max =0;
for(Integer i: resultList){
max = Math.max(i,max);
}
bw.write(max+"");
bw.flush();
bw.close();
}
}시도2
아이템이 주르륵 나열되어있다고 생각하자. 그리고 아이템을 선택하거나 안할수있다.
그리고 선택을 하거나 안할때의 값을 생각해서 둘중에 더 큰것으로 매번 갱신한다면 최종결과를 얻을 수 있다. 하지만 이것을 재귀로한다면 시간초과가 날것이다. 일단 두개를 선택하는 경우에서도 2^n이나옴
dp[i] = dp[i-1]에 관한 식?
i만으로는 부족하다. 하나의 변수가 더있어야한다. 왜냐하면 idx가 -1이되면서 기준값이 되는 weight변수또한 변하기때문이다.
무게k에 들어갈수있는가치 v의 최댓값을 구해야한다.
v를 결과값이라고 생각해보고, 무게를 변수로 생각해보자.
또한 아이디어의 첫 시작이 i번째 물건을 챙길수도있고, 아닐수도있고니까
i와 k의 이차원배열로 만들고 그 결과값이 value여야한다
dp[i][w] = dp[i-1][w-wi]이런식으로 변수 두개를 받는 배열이 필요하다
dp[i][w]: i까지 물건을봤을때의 value의 최댓값.weight는 현재 w
이해안가는점
o(nW)의 시간복잡도를 가지는것은 이해하겠으나 이게 다항함수가 아니라고한다.
왜냐하면 w는 값자체의 범위를 표현하는것이기때문에 값하나를표현하려면
값의개수가 n개라고 했을때 2^n = w이다 (왜지?)
w라는숫자가 들어올때 입력사이즈는 logW이다 (왜지?)
그러니까 o(n*2^n)인것이다
코드
public class Main{
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String input[] = br.readLine().split(" ");
int n = Integer.parseInt(input[0]);
int weight = Integer.parseInt(input[1]);
int dp[][] = new int[n+1][weight+1];
int value[][] = new int[n+1][2];
for(int i=1;i<=n;i++){
String input2[] = br.readLine().split(" ");
int w = Integer.parseInt(input2[0]);
int v = Integer.parseInt(input2[1]);
value[i][0] = w;
value[i][1] = v;
}
//0부터 시작하면 dp[i-1][w]에 접근할떄 예외처리를 해주어야해서
//1부터 시작하게끔 만들음
for(int i=1;i<=n;i++){
for(int w=1;w<=weight;w++){
int valueW = value[i][0];
if(w < valueW) dp[i][w] = dp[i-1][w];
else{
dp[i][w] = Math.max(dp[i-1][w], value[i][1]+dp[i-1][w-valueW]);
}
}
}
bw.write(dp[n][weight]+"");
bw.flush();
bw.close();
}
}9251: LCS
int형으로 배열을 선언하게 되면 값이 0인것들은 모두 무시하게된다. 0일수도있는데..
그럼 재귀호출이 계속쌓이는것이다. 이게 그렇게 문제가 되는줄은 모르겠는데 문제가 되나보다.. 이해가 잘 안가긴한다.
점화식을 보고 그대로 식을 세웠다. 하지만 왜 점화식을 저렇게 세울 수 있는지 잘모르겠다
다시꼭 풀어봐야겠다
