17103: 골드바흐 파티션

시간복잡도

• 1초가 100 000 000번의 연산이니 0.5초는 50 000 000.
• 에라토스테네스의 체 + while문 연산
• nlon(logn)대략 1 000 000 x 상수 + O(n)1 000 000
  정도니까 시간안에 완료될것같다

import java.io.*;
import java.util.Arrays;

public class Main{
    static boolean[] isPrime;
    //1이상, n이하의 수들에대해 소수인지 아닌지를 boolean[] 로 return해주는 함수입니다
    public static boolean[] getPrime(int n){
        //인덱스에 2 를넣으면 2가 소수인지를 판별해주는 배열을 만들고 싶었기에 n+1개를 선언해줍니다
        boolean isPrime[] = new boolean[n+1];
        //일단 소수라고 가정을 해줍니다. 모두 소수라고 가정하고 배수들을 제거해나가는 식으로 풀이할것이기때문
        for(int i=0;i<=n;i++){
            isPrime[i] = true;
        }
        //0은 소수가 아니기에 false를 주기도 했지만, 아래의 for문에서 처리하지 못하는 예외이기때문에 앞에서 false라고 처리를 해주는것입니다
        isPrime[0] = false;
        //1또한 아래 for문에서 구현하게 되면 모든 수를 소수처리해버리기때문에 false라고 처리해줍니다.
        isPrime[1] = false;
        //아래 for문은 누군가를 두번더했을때부터 계산합니다. 하지만 2는 그 계산에 포함되지 않기때문에 예외처리로 true를 넣어줍니다
        isPrime[2] = true;
        //i=2부터(2의 배수들을 제거해나갈거라는 의미) n의 제곱근까지만 수행을합니니다.
        //i=2부터 시작하는 이유는 2의 2배수부터 제거해나가야하기떄문(즉, 짝수제거를해야하기때문)이며
        //i<=n이 아니라 i<=루트n까지만 해도되는이유는 n이 소수가 아니라고 가정할때 n=ab로 나타낼수있고, 필연적으로 a나b둘중하나는 루트엔보다 작거나 같게 됩니다.
        //즉, 작거나 같은수에 대해서만 제거를 진행해도 된다는 의미입니다. 예를들어 a가 작거나 같은값일때, ab = n의 공식에 의해 a의 배수인 ab즉, n은 이미 소수가 아니라고 판별되게 됩니다.
        //즉 ba로인해 얻은 n을 다시 false처리할필요가 없습니다.
        for(int i=2;i<=Math.sqrt(n);i++){
            //소수가 아닌수는 그 수를 인수분해했을때, 더작은값으로 이미 그 수의 배수들이 false처리됐을것입니다.
            //예를들어 2의 배수(짝수)는 모두 false처리된 후에 2의 또다른 배수인 4의 배수는 2의 배수안에 모두 포함이 되는것을 확인할 수있습니다.
            if(isPrime[i]){
                //k는 넘어온 수의 두배수를 해주고 매번 i씩더해서 3배수,4배수...를 모두 확인합니다. 그리고 그 곱한수 k가 매번 n보다는 작거나 같아야합니다
                //인수가 k보다 클일은 없을테니까요
                for(int k=i+i;k<=n;k+=i){
                    isPrime[k] = false;
                }
            }

        }

        return isPrime;
    }
    public static void goldBach(int n){
        //2로잡는이유는 가장작은 소수가 2이기때문입니다
        int s = 2;
        //n-2로 잡은이유는 s+e = n이기때문입니다. e는 소수가 아닐지도 모르지만 그점은 아래while문에서 확인할것이며
        //일단 s와 e의 합을 n으로 유지시켜주면서 양쪽값을 늘리고 줄이면서 전체값을 확인해보는 로직입니다.
        int e = n-2;
        //파티션의 개수를 셀 변수를 선언합니다
        int count =0;
        //예를들어 s=e일수도있으니 등호까지 붙여줍니다. 
        //저 조건을 벗어나게 된다면 똑같은 경우를 또세게됩니다. 그리고 끝이 나지 않게 됩니다. 그래서 저조건을 추가시켜줬습니다.
        //왜 똑같은 경우를 또세게되냐면 s=3, e=5이여서 3+5나 5+3이나 같은 파티션으로 취급되기때문이죠
        while(s<=e){
            //둘이 더했을떄 n이되는것은 필연적일테니. 둘다 소수인지만 확인해주면됩니다
            if(isPrime[s] && isPrime[e]) count++;
            //아래명령문을 추가시켜줌으로써 while문이 끝날수있게 해줍니다
            s++;
            e--;
        }
        System.out.println(count);
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        //isPrime에 대해 반복적으로 사용할것이기때문에 goldBach에서 매번 getPrime을 호출하지 않고, 최대입력값에 대해서 미리 구해놓고 미리구해놓은 값을
        //재사용하는 방식을 사용한다
        isPrime = getPrime(1000000);
        //입력받은 n 에 대해 n번의 입력을 추가로 받는다
        for(int i=0;i<n;i++){
            int x = Integer.parseInt(br.readLine());
            //입력받은 수에 대해서 매번 골드바흐의 파디션의 개수를 구합니다
            goldBach(x);
        }

    }


}

17087: 숨바꼭질6

풀이

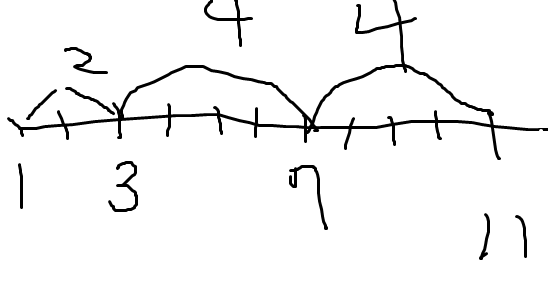
1초후에 1칸을 간다고 치면 동생을 찾을수있긴하다.
근데 내가 만약 5칸을 간다고하면 나는 앞뒤로 +-5칸만이동할수있으니 1에 절대 도달할수없다. 즉 절대 동생을찾을수없다. +-5칸이라는게 한칸씩방문하면서 5칸을가는게 아니라 순간이동개념이다.
그래서 3과의 차이인 2 4 4 의 최대공약수를 구해야한다
저 차이 2,4,4 가 각각 D로 나뉘어져야 도달할수가있다.
1초후에 D, 2초후에 2*D 3초후에 3D인데 이 값이 2,4,4가 될 수 있어야지 동생을 찾을 수 있기 때문이다.

코드

import java.io.*;
import java.util.Arrays;

public class Main{
    //유클리드호제법을 이용하여 최대공약수를 구한다
    public static int gcd(int a, int b){
        //큰수로 작은수를 나누기위해서 큰수를 big에 저장하고
        int big = a>b?a:b;
        //작은수는 sma에 저장한다
        int sma = a>b?b:a;
        //나눠서 sma가0이 되면 조건문을빠져나올건데, sma의 바로 전값을 return해줘야한다
        //그래서 temp를 정의한다
        int temp =1;
        while(sma !=0){
            temp = sma;
            //나머지를 두번쨰 값에 저장한다
            sma = big % sma;
            //기존두번째값은 첫번째 값이 된다
            big = temp;
        }
        return temp;
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String input[] = br.readLine().split(" ");
        int n = Integer.parseInt(input[0]);
        int s = Integer.parseInt(input[1]);
        int arr[] = new int[n];
        String num[] = br.readLine().split(" ");
        for(int i=0;i<n;i++){
            int x = Integer.parseInt(num[i]);
            //차이를 저장한다. 하지만 차이는 음수가 되면 안된다. 절댓값을 저장해야한다. 그림에서 보여준것처럼 두 거리가 몇칸이떨어져있느냐를 저장하고
            //그 값의 최대공약수를 구해야한다
            if(x > s) arr[i] = x-s;
            else arr[i] = s-x;
        }
        //정렬하는이유는 아래 FOR문에서 음수가 나오지 않게하려고이다.
        Arrays.sort(arr);

        //일단 첫번쨰 값을 넣고 그 다음값, 그다음값 을 돌면서 최대공약수를 구한다
        //a와 b의 최대공약수 c가 있다고하자. 그리고 c와 d의 최대공약수 e를 구하면 이 e는 a,b,c의 최대공약수라고 말할수있기때문이다.
        //왜냐하면 c는 a로도 나눠지면서 b로도 나눠지는 가장큰수를 대표하는 수이기때문이다.
        int result = arr[0];
        for(int i=1;i<arr.length;i++){
            result = gcd(result, arr[i]);
        }
        System.out.println(result);
    }


}

2824:최대공약수

https://velog.io/@gglifer/%EB%B0%B1%EC%A4%80-2824-%EC%B5%9C%EB%8C%80%EA%B3%B5%EC%95%BD%EC%88%98