10974: 모든순열

이전처럼 푸는문제라고생각했다.
근데 이번에는 순서를 바꿔야하는 문제이다.
예전에는 "조합"을 풀었다면 이번엔 "순열"을 계산해야하는문제였다.
둘의 차이는 알지만 코드적으로는 어떤차이가있을까?
에 대해 궁금해졌다.

기존코드를 분석해보자.

기존코드1

 public static void permutation(int n, int idx, int count, String str){
        if(count==n){
            System.out.println(str);
            return;
        }
        if(count > n || idx > n) return;
        if(str.isEmpty()) permutation(n,idx+1,count+1, idx+"");
        else permutation(n,idx+1,count+1, str + " " + idx);
        permutation(n,idx+1,count, str);

    }

• 이코드는 왜 조합에는 사용가능하지만 순열에서는 사용할 수 없을까?
• 조합 - 순서상관없으며 여러개중에 내가 뽑을 개수가 정해져있고 다 뽑고 나면 종료해야함
• 순열 - 순서가 중요하다. 주어진 숫자를 모두사용해서 순서만바꾸어야한다
• 위의코드는 계속해서 idx가 증가한다. 조합에서는 이게 가능했다. m개중n개를 고르는게 조합인데, 보통 m>n이기때문이다. 그래서 idx를 계속증가시켜도된다. 계속증가시켜서 n보다 큰 값이 된대도 증가시켜도된다. idx>m까지 이기만 하면되고, cnt가n이여야한다.

기존코드2

import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
import java.util.stream.Collectors;

public class Main{
    public static void dfs(int n, int m, int depth, int idx, String str){
        //깊이가 m일때 출력한다. 깊이가 m이라는것은 내가 출력한것의 개수가 m개라는의미이다.
        if(depth==m){
            System.out.println(str);
            return;
        }
        for(int i=idx;i<=n;i++){
            //아래의 idx로 넘겨주는것이 idx가 아니라 idx+1이여야한다
            //그래야 중복이 안생긴다. i+1이라는것은 무조건 내가 들어온 idx랑 겹칠일이 없으니까
                if(!str.isEmpty()) dfs(n,m,depth+1,i+1, str + " " + i);
                else dfs(n,m,depth+1,i+1, "" + i);

        }

    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String input[] = br.readLine().split(" ");
        int n = Integer.parseInt(input[0]);
        int m = Integer.parseInt(input[1]);
        dfs(n,m,0,1,"");
    }


}

N과M vs 모든순열

N과M

• 순서는 오름차순으로 정해져있기때문에 nCm을 고르는 것과 같다
• 순서가 오름차순이라는말은 내가 바라보는 수가 매번 증가해도된다는 소리다. 그러니까 1 -> 2 -> 1로 갈일이없다. 하지만 모든순열의 경우는 다르다. 그렇게 숫자가 작아질일이있다.

모든순열

• 순서가 바뀔수있다. 순서가 바뀌는것은 for문으로 해결한다.
  for문과 printed된 여부를 확인하는 boolean []을 통해서

조합의 특징 (mCn)

• idx > m
• cnt = n
• 일단 1을 선택한다 그리고 선택하지 않을수도있다. 1부터 idx를 하나씩 늘려나가면서 내가 선택한 숫자가 6개가 되면 종료한다

순열의 특징 nPn

• idx는 계속증가하기만하면되는게아니다. 증가했다가 또다른숫자를 가리키거나 해야한다. 이런부분은 idx가 변화한다기보단 메서드가 끝나면서 메서드1idx1 -> 메서드2idx2 를 가리키게 해야한다는 의미다
• idx는 1~n중 하나를 선택해야하고, 한번씩만 선택돼야한다 -> 이를 도와주기위해서는 이미 출력되었다는것을 알려줄 변수가 필요하다 -> boolean []필요
• cnt = n

코드

import java.io.*;
import java.util.List;
import java.util.Stack;
import java.util.stream.Collectors;

public class Main{
    static boolean isPrinted[];
    //순열 -> 재귀호출로 여러경우를 다 탐색하되, 조건이 맞는 경우만 출력을 하는 풀이를 생각했음
    public static void permutation(int n, int depth, String str){
        //깊이가 n이될때까지 출력을 계속한다. 깊이가 n이라는것은 내가 출력하는 것의 개수가 n개라는것이다. 그때가 되면 출력을한다.
        //깊이는 0부터시작하기때문에 깊이가 n이될때 n개의 출력을 갖는다
        if(depth == n){
            //str에 내가 출력할 값들을 미리 더해놨었다. 그냥 출력만하면된다
            System.out.println(str);
            //재귀함수를 사용할땐 종료조건이 있어야한다.
            return;
        }
        //i=1부터 시작하는이유는 str에 추가되는 숫자가 매번 달라지기 때문이고, 이 값이 작아질수도있다. 그래서 1부터시작한다 단, 내가 이미 출력한 변수는 isprinted[] = true;
        //로 설정해두고 그 숫자는빼고 다른숫자들에 대해 살펴본다(재귀함수로 출력하려한다)
        for(int i=1;i<=n;i++){
            //아래두줄의 명령문으로 인해 재귀호출이 반복적으로 일어나더라도 매번i=1만 참조하는것을 방지할수있음
            if(!isPrinted[i]){
                //내가 당장 i=1에 들어왔다. 하면 i=1에 대해서 출력했다고 처리해준다. 왜냐하면 재귀함수호출시 i를 더해줄것이기때문이다.
                //재귀함수안에들어가서는 i=1을또 출력하면안되기때무에 일단 true라고해준다. for문안의 조건문안으로 들어가면 안되기때문에.
                isPrinted[i] = true;
                //매번 깊이는 +1을해줘서 숫자의 개수가 depth=n이 되면 출력.
                //str이 아예비어있을경우 str + " " + i를하게되면 한칸띄고 i가 출력돼서, 예외처리를 해두었다. 
                if(!str.isEmpty()) permutation(n, depth+1, str +" "+ i);
                else permutation(n, depth+1, ""+ i);
                //아래의 코드를 쓴 이유는 내가 가지고있는 str은 i가 없는 str이다. 그러니까 결국 다음for문이 동작하고, i=2로 들어가서 재귀함수를 호출할떄 
                //그 재귀함수에서는 지금 i에 접근할 수 있어야한다. 그런부분을 고려하여 false처리를 해주었다
                //여기서 false처리를 해주지않게되면 for문 한번만 돌면 모든 원소에 대해 isprinted가 true가 돼버려서 출력할수없게된다.
                isPrinted[i] = false;
            }

        }


    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        isPrinted = new boolean[n+1];
        permutation(n,0, "");
    }


}

2407:조합

import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
import java.util.stream.Collectors;

public class Main{
    public static long combination(int n, int r){
        if(n==r) return 1;
        if(r==1) return n;
        if(r==0) return 1;
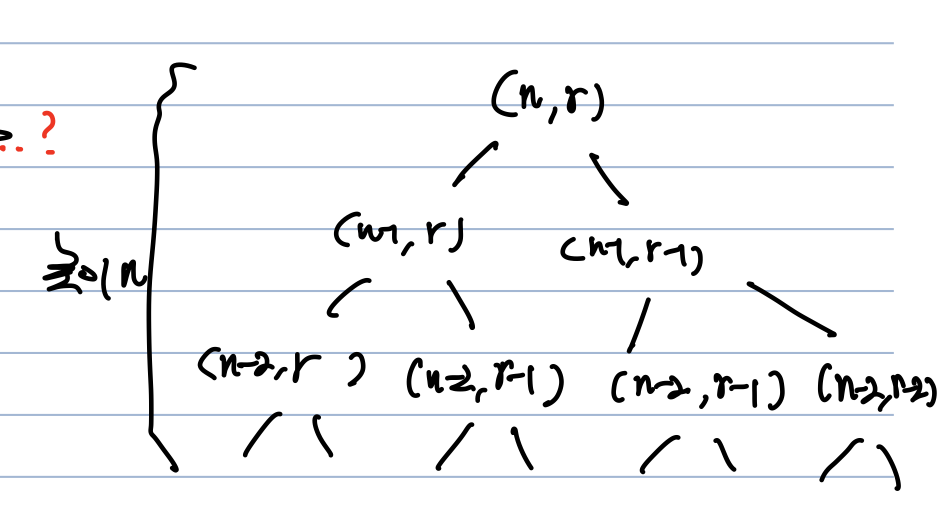
        return combination(n-1, r-1) + combination(n-1,r);
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String input[] = br.readLine().split(" ");
        int n = Integer.parseInt(input[0]);
        int m = Integer.parseInt(input[1]);
        System.out.println(combination(n,m));
    }
}

• 점화식을 그대로 이용하면 시간초과가난다 -> 2^n
  

2981: 검문

풀이

문제의 요구사항을 식으로 정리하면 다음과 같다.
6 / M + r
34 / M + r
38 / M + r
에서 r은 같고 우리는 M을 찾아야한다.
찾고싶은것이 M이기때문에 식을 M = ?으로 만들어야한다.
저 식은 M,r이 공통이기때문이 묶을 수 있다
6/M + r = 34 / M + r
이 식을봤을떄
(6-34) = M이라는 식이 완성된다
우리는 이 식을 만족하는 M을 오름차순으로 출력해야한다.
근데 이식만 만족해야하는게 아니라
34 / M + r = 38 / M + r 이 식도 만족해야한다.

방금 내가 한 두가지 과정을 변수를 넣어 설명해본다면 아래와 같다.
"입력받은 i+1번쨰숫자 - i번째숫자의 공통적인 약수를 찾으면된다."
이 숫자의 최대공약수를 찾고, 최대공약수의 약수를 찾기만하면
공통적인 약수를 오름차순으로 만드는게 가능하다

a1, a2 최대공약수를 x를 구했어 그의미는 다음과 같음
-a1이랑도 나눠짐
-a2랑도 나눠짐

• 그리고 젤큼

a2-a3은 결국 M을 의미함
(a2-a3 = M)

x와 M의 gcd를 구한다는 것의 의미

• a1,a2로 나눠지는 값 x과
  M(a2,a3으로 나눠지는 값)
  의 최대공약수를 구하면
  넷다 나눠지는 수중, 최대값을 구하게 되는것임
  왜냐면 공약수를 구한다는 행위 = 넷다나눠지는 수를 구한다
  최대공약수를 구한다는 행위 = 그 공약수를 모두 아우르는 값 하나를 뽑는다

https://st-lab.tistory.com/155

import java.io.*;
import java.math.BigInteger;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;
import java.util.stream.Collectors;

public class Main{
    public static int gcd(int a, int b){
        //큰값나누기 작은값을하기 위해 작은값과 큰값을 계산해서 넣어준다
        int bigger = a>b?a:b;
        int smaller = a>b?b:a;
        //smaller가 0이 되기전의 temp를 return해주어야한다
        int temp = 0;
        //두번째수가 0이될때까지 while문을 반복한다.
        //나머지를 두번째수에 저장하고, 원래두번째에 있던 수는 식의 첫번쨰로 옮겨준다
        while(smaller!=0){
            temp = smaller;
            smaller = bigger % smaller;
            bigger = temp;
        }
        return temp;

    }
    public static void divisor(int a){
        //약수중 1은 제외한다. 그리고 본인(최대공약수 a)는 출력한다
        for(int i=2;i<=a;i++){
            if(a%i==0){
                System.out.print(i + " ");
            }
        }
        System.out.println();
    }
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int arr[] = new int[n];
        for(int i=0;i<n;i++){
            arr[i] = Integer.parseInt(br.readLine());
        }
        //정렬: "i번쨰와 i+1번쨰 수의 차이"의 최대공약수를 구해야하는데 이 결과가 음수이면 안되기떄문에
        Arrays.sort(arr);
        //초기값을 세팅해준다.
        int s1 = arr[0];
        int s2 = arr[1];
        //오름차순이면 뒤쪽에 있는게 값이 클테니 s2-s1을해준다
        int result = s2-s1;
        //방금 arr0,1에대한 계산을 마쳤으니 i=2부터 계산해준다.
        //result는 처음에는 arr[1]-arr[0]이지만 그 이후로부터는 인접한 두 값의 차이에 대해 최대공약수를 구한 수이다.
        //그 수는 그 수를 대체할 수 있다. 즉, 앞선 i=2일때 result가 gcd연산에 의해 어떠한 x값이 얻어졌다고 가정한다
        //이 값. 즉 최대공약수는 i=0,i=1에 대해 공통적으로 나눠지는 수를 의미하게 되니까.
        for(int i=2;i<n;i++){
            result=gcd(result, arr[i]-arr[i-1]);

        }
        //약수를 구하는 메서드
        divisor(result);

    }


}