노드의 구조

static class Node<E>{
        E value;

        Node<E> left;//왼쪽자식
        Node<E> right;//오른쪽 자식
        Node<E> parent;

        Node(E value) {
            this(value, null);
        }

        Node(E value, Node<E> parent) {
            this.value = value;
            this.parent = parent;
            this.right = null;
            this.left = null;
        }

    }

말로 설명

1. 삽입
2. 삭제
3. 탐색(전위, 후위, 중위)

재귀로 구현해보자

삽입

추가한Node insert(root, 찾을 data)
1) root == null

• 새로운 노트를 루트에 넣는다
  2) data < root.data
  -> root.left에 data를 추가해야함 그래서 추가된 Node를 root.left에도 추가시켜야겠지
  insert(root.left,data)를 하면 root.left를 root라 가정하고 data을 넣을거임
  3) data > root.data
  -> root.right에 data를 추가해야함. 이때는 root.right를 다시 root로 가정하고 data를
  삽입해서 그 끝에 추가된 data를 넣어준다

1)에서는 새로운 노드를 루트에 넣고 바로 반환하는데 2),3)은 재귀가 끝나고 나서..
root에 대한 node를 반환하면 됨.
즉, 이 insert는 root에 대해 data를 추가했을때의 root를 반환하는 함수인거임

삭제

어떠한 데이터를 삭제하고싶다
1) root==null 일경우

• 삭제할 수 없다. root를 return한다
  2) data < root.data
• 내가 삭제하려는 데이터는 root.leftchild에 있을 것이다. 그쪽을 탐색해야한다
  3) data > root.data
• 내가 삭제하려는 데이터는 root.rightchild에 있을 것이다. 그쪽을 탐색해야한다
  4) data == root.data
• 내가 삭제하려는 데이터를 찾았다
  4-1) 내가 삭제하려는 node는 자식이 없다
• null을 리턴하자. 그러면 이node의 부모가 얘를 삭제해준다
  4-2) 내가 삭제하려는애가 right노드만 가지고 있다.
• 그 right노드를 그대로 돌려주자. 왜 그래도 되냐면. 만약 왼쪽값을 위에 넘겨준다치자
  어차피 부모하위에 있다는것은 루트노드보다 크거나 작다는걸 만족시킨다는거고.
  동일선상에있는 노드랑 비교한대도 중간으로 가는것은 문제되지 않으니 그냥 return해도된다

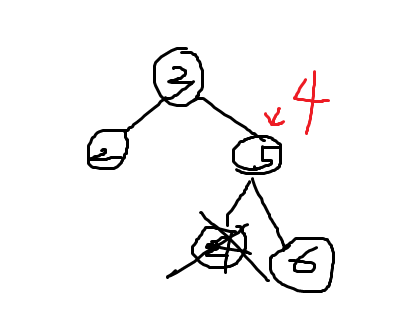
4-3) 내가 삭제하려는 애가 자식노드가 다 있다

• 일단 내가 삭제하려는 애의 오른쪽 서브트리중에 제일작은놈을 찾는다
• 내가삭제하려는 놈은 root이다
• 내가 찾은 가장 작은 놈을 찾아서 그놈의 data를 현재 내가 삭제하려는 놈의 data에 붙여넣는다
• 기존의 가장 작은놈은 삭제해버린 뒤에 root.right에 넣어준다
  왜냐면 delete(a,b)하면 a를 root로하는 서브트리에서 b와 일치하는것을 삭제한 뒤에 a를 반환하기 때문에 삭제된
  서브트리를 반환해줄것이기 때문이다.

findmin

• 가장작은 data를 return해주는 함수
• root의 left가 null이 아닐때까지 계속 root를 파고들어가서 그 root가 가지고있는 data를 return한다

코드

static class BinarySearchTree{
        Node root;
        static class Node {
            int value;
            Node leftChild;
            Node rightChild;

            public Node(int value) {
                this.value = value;
                this.leftChild = null;
                this.rightChild = null;
            }
        }
        public Node insert(Node root, int value){
            if(root==null){
                root = new Node(value);
                return root;
            }
            if(value < root.value){
                root.leftChild = insert(root.leftChild, value);
            }
            if(value >= root.value){
                root.rightChild = insert(root.rightChild, value);
            }
            return root;
        }
        public Node delete(Node root, int value){
            if(root==null) return root;
            if(root.value < value){
                root.rightChild = delete(root.rightChild, value);
            }
            if(root.value > value){
                root.leftChild = delete(root.leftChild, value);
            }
            if(root.value == value){
                if(root.leftChild==null && root.rightChild==null) return null;
                if(root.leftChild==null) return root.rightChild;
                if(root.rightChild== null) return root.leftChild;
                //둘다 존재할 경우
                int min = getMin(root.rightChild);
                root.value = min;
                root.rightChild = delete(root.rightChild, min);
            }
            return root;
        }
        public int getMin(Node root){
            int min = root.value;
            while(root.leftChild!=null){
                root = root.leftChild;
                min = root.value;
            }
            return min;
        }
    }

순회방법

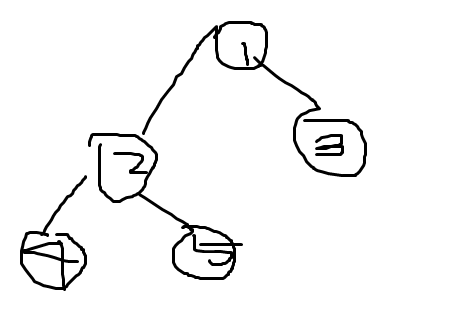
1) inorder 4-2-5-1-3
1. left
2. root(자기자신)
3. right
2) preorder 1-2-4-5-3
1. root
2. left
3. right
3) postorder 4-5-2-3-1
1. left
2. right
3. root

코드

 public void inOrder(Node root){
            if(root != null){
                inOrder(root.leftChild);
                System.out.println(root.value);
                inOrder(root.rightChild);
            }
        }
        public void preOrder(Node root){
            if(root != null){
                System.out.println(root.value);
                preOrder(root.leftChild);
                preOrder(root.rightChild);
            }
        }
        public void postOrder(Node root){
            if(root!=null){
                postOrder(root.leftChild);
                postOrder(root.rightChild);
                System.out.println(root.value);
            }
        }

---

출처
https://zeddios.tistory.com/492 << 그림보면서 설명