DFS 알고리즘 (+백준 1260번)

개념

깊이 우선 탐색 (depth First Search), DFS 알고리즘은 맹목적 탐색 기법 중 하나이다.

맹목적 탐색 기법이란,
정해진 순서에 따라 상태 공간 그래프를 점진적으로 생성해가면서 해를 탐색하는 방법이다.

맹목적 탐색 기법에는 깊이 우선 탐색, 너비 우선 탐색, 반복적 깊이심화 탐색 등이 있으며
이 글에서는 깊이 우선 탐색을 설명할 것이다.
(너비 우선 탐색은 여기 -> https://velog.io/@fluid_silver/BFS-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98)

먼저 그림을 보자. (출처 : 학교 수업 pdf)

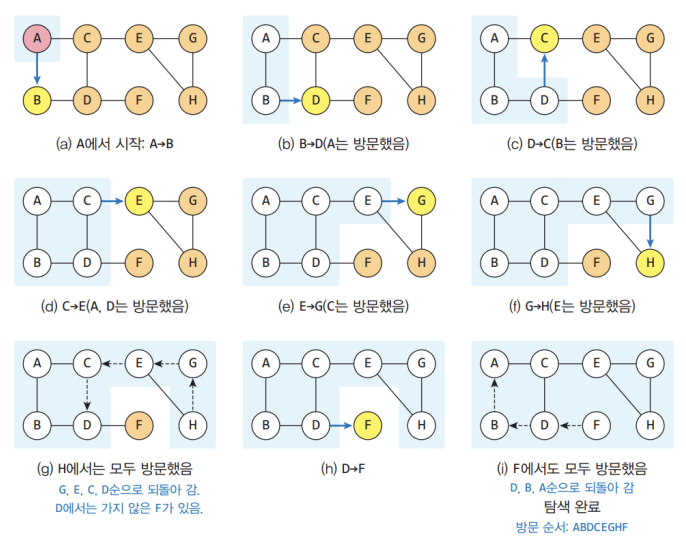
한 방향으로 끝까지 가다가 더 이상 갈 수 없게 되면
가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색을 진행하는 방법이다. (백트래킹)

목표 정점이 있다면, 모든 정점을 방문하지 않고 목표 정점에 도달했을 때 종료한다.
스택(stack)을 사용하여 구현한다.

알고리즘

1. 시작 정점을 스택에 저장
2. 스택의 맨 뒤 정점의 이웃을 neighbor에 저장
3. neighbor 중에 방문하지 않은 정점 하나를 택하여 스택에 저장,
   모두 방문한 정점인 경우 선택된 정점을 스택에서 제거
4. 2~3 과정을 반복
5. 스택에 포함된 정점이 없을 때 알고리즘을 마침

코드

백준 1260번 DFS와 BFS : https://www.acmicpc.net/problem/1260

C++

#include<iostream>
#include<vector>
#include<map>
#include<stack>
#include<algorithm>
using namespace std;
typedef struct Node Node;
struct Node {					// Node
	int data = 0;
	Node* next = NULL;
};
int main() {
	int N, M, V;
	cin >> N >> M >> V;
	vector<Node> head(N + 1);
	for (int i = 0; i < M; i++) {
		int a, b;
		cin >> a >> b;
		Node* tmp = new Node();	// linked list
		tmp->data = b;
		tmp->next = head[a].next;
		head[a].next = tmp;
		Node* tmp2 = new Node();
		tmp2->data = a;
		tmp2->next = head[b].next;
		head[b].next = tmp2;
	}
	stack<int> s;
	map<int, int> visited;		// 방문한 정점 저장
	s.push(V);
	cout << V << " ";
	visited.insert({ V, 1 });
	while (size(s) != 0) {		// 스택에 정점이 없을 때까지
		int curr = s.top();		// 스택의 맨 뒤 정점
		Node head_tmp = head[curr];
		vector<int> neighbor;
		while (head_tmp.next != NULL) {	// 이웃 정점 저장
        	head_tmp = *head_tmp.next;
			neighbor.push_back(head_tmp.data);
		}
        if (size(neighbor) == 0) {
        	s.pop();
        }
		sort(neighbor.begin(), neighbor.end());	// 번호가 작은 것 방문
		for (int i = 0; i < size(neighbor); i++) {
			if (visited.find(neighbor[i]) == visited.end()) {	// 방문하지 않은 정점
				s.push(neighbor[i]);		// 스택에 저장
				cout << neighbor[i] << " ";
				visited.insert({ neighbor[i], 1});
				break;
			}
			else if (i == size(neighbor) - 1) {		// 모두 방문한 정점인 경우
				s.pop();				// 정점 제거
			}
		}
	}
	return 0;
}

Python

# 나중에 추가해보겠음

특징

DFS는 메모리 공간 사용이 효율적이지만
목표 정점을 찾으면 종료하기 때문에 최단 경로는 보장할 수 없다.