순열과 조합
순열
: 서로 다른 n개의 원소를 가지는 집합에서 중복 없이 순서에 상관있게 r개의 원소를 선택하거나, 나열하는 것이다.
= n개의 원소로 이루어진 집합에서 r개의 원소로 이루어진 부분집합을 만드는 것과 같다.
- 순열은 조합과 달리 순서를 따져 부분집합을 만든다.
3개의 원소로된 집합에서 2개의 원소를 선택하는 경우의 수
3 * 2 = 6
조합
: 서로 다른 n개의 원소를 가지는 어떤 집합에서 중복 없이 순서에 상관없게 r개의 원소를 선택하는 것
= n개의 원소로 이루어진 집합에서 r개의 원소로 이루어진 부분집합을 만드는 것과 같다.
3개의 원소로된 집합에서 2개의 원소를 선택하는 경우의 수
(3 2) / (2 1)= 3
GCD와 LCM
최대공약수(Greatest Common Divisor, GCD)
공약수(Common Divisor)
: 공약수는 두 수 이상의 여러 수 중 공통된 약수를 의미한다.
=> 여러 개의 공약수 중 최대인 수가 바로 최대공약수이므로, 6과 9의 최대공약수는 3이다.
최소공배수(Lowest Common Multiple, LCM)
공배수 (Common Multiple)
: 공배수는 두 수 이상의 여러 수 중 공통된 배수를 의미한다. 12와 18 두 수의 최소공배수는 36이다.
유클리드 호제법
GCD와 LCM 개념이 쓰이는 문제를 풀 때 가장 많이 쓰이는 유클리드 호제법.
유클리드 호제법은 최대공약수와 관련이 깊은 공식이다. 2개의 자연수 a와 b가 있을 때, a를 b로 나눈 나머지를 r이라 하면 a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 이론이다.
이러한 성질에 따라 b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나누는 과정을 반복해, 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수임을 알 수 있게 된다.
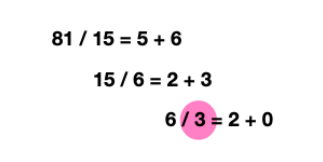
81과 15를 같은 방식으로 쭉 나눴을 때, 마지막 나눗셈에서 나누는 수인 3이 최대공약수임을 확인할 수 있다.
=> 이런 식으로 유클리드 호제법을 이용하게 되면 최대공약수를 쉽게 구할 수 있게 되고, 최대공약수를 구할 수 있게 되면 최소공배수는 자연스럽게 구할 수 있게 된다.
멱집합
: 어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합 이라고 한다.
: 멱집합은 원소가 있는지, 없는지의 2가지의 경우를 고려하기 때문에 집합의 요소가 n개일 때 모든 부분집합의 개수는 2의 n제곱개다.
집합 {1, 2, 3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 으로 나열할 수 있고, 이 부분집합의 총 개수는 8개다. 모든 부분집합을 통틀어 멱집합이라고 한다.
Step A: 1을 제외한 {2, 3}의 부분집합을 나열합니다.
- Step B: 2를 제외한 {3}의 부분집합을 나열합니다.
-- Step C: 3을 제외한 {}의 부분집합을 나열합니다. → {}
-- Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열합니다. → {3} - Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열합니다.
-- Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열하려면, {}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열합니다. → {2}, {2, 3}
Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열합니다.
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열합니다.
-- Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열합니다. → {1}, {1, 3}
-- Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 2, 3}을 추가한 집합들을 나열합니다. → {1, 2}, {1, 2, 3}
멱집합을 구하는 방법에서 각 단계를 유심히 살펴보면, 순환 구조를 띤다.
여기서 순환구조는 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법
따라서, 문제를 작은 단위로 줄여나가는 재귀를 응용할 수 있습니다. 예를 들어 PowerSet 이라는 멱집합의 개수를 리턴하는 함수를 작성한다면, PowerSet 함수에서 자기 자신을 호출하며 문제를 더 작은 문제로 문제의 크기를 줄여 해결할 수 있다. 문제가 가장 작은 단위로 줄어들고, 함수가 리턴될 때 카운트를 올리는 방식으로 멱집합의 개수를 구할 수 있다.
