Demand Paging

: 요청이 있으면 그 page를 메모리에 올리겠다는 뜻.
paging 기법은 프로그램이 실행될 때 그 프로세스를 구성하는 주소공간을 전부 한꺼번에 메모리에 올리는게 아니라 demand paging 기법을 사용한다.
paging 기법에서 각각의 page table entry마다 valid/invalid bit이 있음.
Memory에 없는 Page의 Page Table
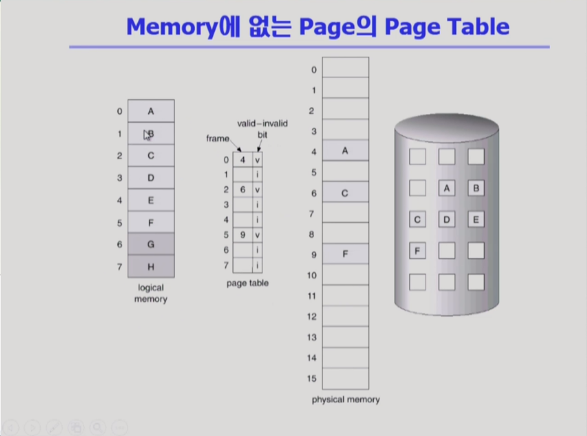
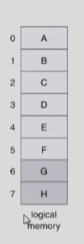
하나의 프로그램을 구성하는 논리적인 메모리.
- 여러개의 page들로 구성이 되어있음.
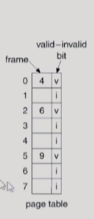
page table을 통해서 page에 대한 주소변환 정보가 담겨있음.
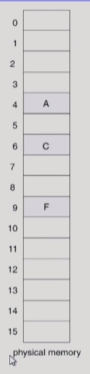
물리적인 메모리가 주어져있음.

disk, backing store, 즉 swap area라고 하는 부분이 있음.
그래서, 프로그램을 구성하는 이 page들 중에서 당장 필요한 부분은 demand paging에 의해서 물리적 메모리에 올라가 있을 것. 그렇지 않은 부분은 Swap Area에 내려가 있게 된다.
-
물리적 메모리에 올라간다면 page table의 valid로 표시. 주소 변환 정보가 의미있는 값이 들어가 있음. 반면에, 나머지 page들은 물리적 메모리에 안올라가 있고, backing store에 내려가 있기 때문에 invalid로 표시되어 있다.
-
사용되지 않는 주소 영역도 invalid라고 표시됨.
- 프로그램을 구성하는 페이지는 사실 A~F까지임. G,H는 사용이 안되는 page인데 주소 공간에서 이만큼의 주소 영역을 지원해주는 것임.
page fault
: 해당 페이지를 물리적 메모리에 접근하려고 page table에서 주소를 보려고 하는데 invalid 값이 set되어 있다면, page fault가 난다.
- page fault가 나면 cpu는 자동적으로 운영체제한테 넘어감. 운영체제가 cpu를 가지고 fault난 page를 메모리에 올리는 작업이 필요하다. page fault에 대한 처리 루틴이 운영체제에 정의 되어 있음.
=> trap이 걸린다고 표현하고, 일종의 sw interrupt라고 할 수 있음.
Page Fault

Steps in Handling Page Fault
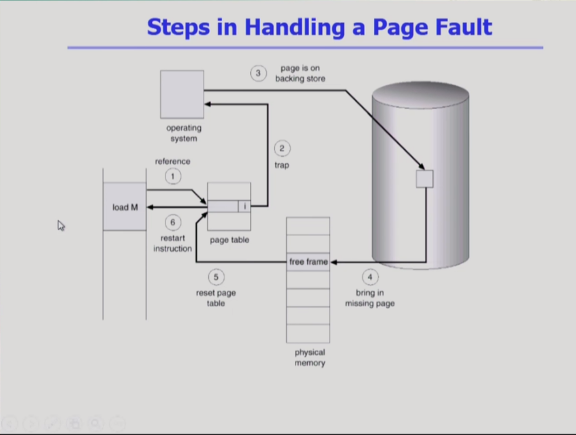
1. 메모리 reference가 있었는데, 주소 변환을 하려고 봤더니, invalid로 표시. 이 page가 메모리에 올라와있지 않다는 뜻.
2. trap이 걸려서 cpu가 운영체제한테 자동으로 넘어간다.
3. 운영체제는 backig store에 있는 page를,
4. 물리적인 메모리에 올려놓는다. 만약에 빈 page frame이 없으면 무언갈 쫓아내고 넣음.
5. 해당하는 frame 번호를 entry에다가 적어놓고 valid로 바꾼다.
6. 나중에 cpu를 다시 얻어서 주소 변환을 하게되면 valid로 되어있고, 주소변환을 정상적으로 해서 해당하는 물리적인 메모리의 page frame에 접근할 수 있게 된다.
Performance of Demand Paging

그런데 page fault가 났을때 디스크에 접근하는 것은 대단히 오래 걸리는 작업이다.
page fault가 얼마나 나느냐에 따라서 메모리 접근 시간이 크게 좌우된다.
page fault의 비율을 0에서 1사이의 값임
- 0: 절대 page fault가 안남.
- 1: 매번 메모리 참조할 때마다 page fault난다.

실제 page fault가 얼마나 나는지 계산했을 때 거의 이 범위 내에서 난다.
거의 안난다는 뜻. page default가 나지 않고, 직접 메모리부터 직접 주소 변환 할 수 잇음.
메모리 접근 시간을 page fault까지 감안해서 계산해보자.
- (1-p): page fault가 안나는 비율 => 메모리 접근하는 시간만 걸림.
- p: page fault가 나는 비율
- OS & HW page fault overhead : 운영체제에 cpu가 넘어가서, hw적으로 page fault를 처리하는 overhead
- swap page out if needed : 메모리에 빈 공간이 없으면 어떤 page 하나를 쫓아내고,
- swap page in : 그 자리에 disk에서 읽어온 page를 올려놓는다.
- OS & HW restart overhead : os가 page table valid 로 표시하고, 나중에 cpu를 얻으면 restart 한다.
Free Frame이 없는 경우
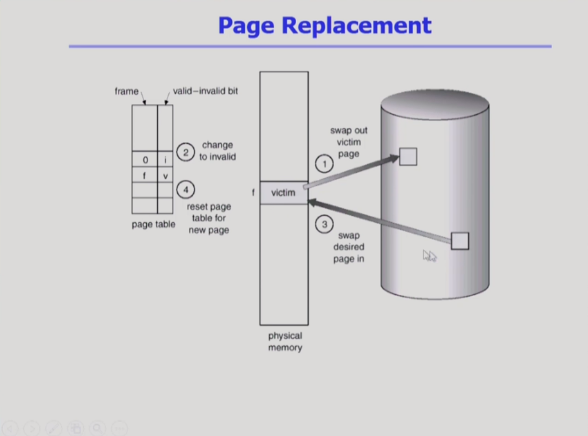
Page replacement
빈 page frame이 없을 때 어떤 frame을 빼앗는 것
앞으로 이 replacement 알고리즘에 대해 알아보자 ~~
reference string
: 페이지들에 서로 다른 번호를 붙여놓고, 시간 순서에 따라서 참조된 순서를 나열한 것.
Page Replacement

-
어떤 것을 쫓아낼지 결정하고,
-
디스크로 쫓아낸 후,
-
만약 디스크로 쫓아내기 전, 내용이 변경됐다면 (write), 변경된 내용을 backing store에 써줘야 한다. 변경된 내용이 없다면 그냥 지워버리면 됨.
-
쫓겨난 page의 entry에는 bit를 invalid로 바꿔준다.
-
메모리에 올라온 page의 frame 번호를 entry에 적어주고, bit를 valid로 바꿔준다.
Optimal Algorithm
최적의 알고리즘임.
: page fault를 가장 적게함.
- 실제 시스템에서는 미래를 알 수 없으니 사용 x
- 미래 참조될 page 다 안다고 가정
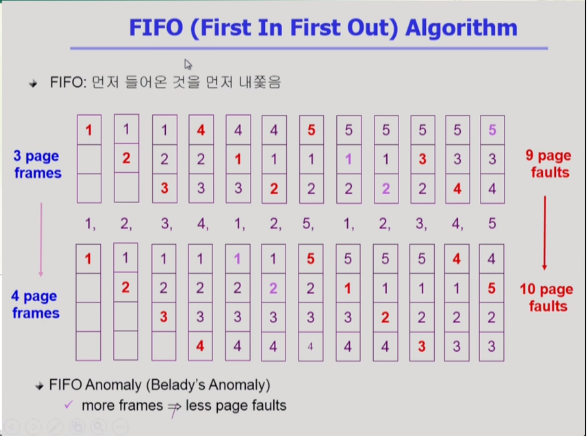
FIFO(First In First Out) Algorithm
FIFO Anomaly
: 그런데 이 알고리즘은 메모리를 늘리면 성능이 좋아져야 하는데, 즉, page fault가 적어져야 하는데 되려 늘어날 수 있음.
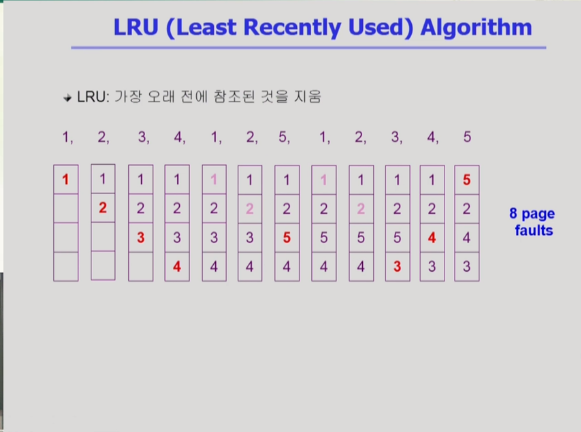
LRU(Least Recently Used) Algorithm

- 가장 메모리 관리나 제일 많이 쓰이는 알고리즘이다.
:최근 참조된 page가 바로 참조될 가능성이 높음.
LFU(Least Frequently Used) Algorithm

: 가장 덜 빈번하게 사용된 page 쫓아내자.
LRU와 LFU 알고리즘 예제
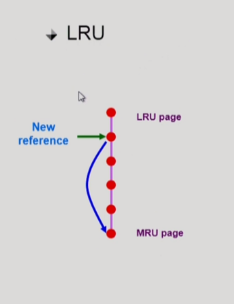
LRU와 LFU를 비교해보자.
LRU와 LFU 알고리즘의 구현
LRU 알고리즘은 참조 시간에 따라서 한줄로 줄세우기 함.
- 다시 참조할 때는 맨 밑으로 보냄.
- 쫓아내야 할 때는 제일 위에꺼를 쫓아냄.
- 시간 복잡도 O(1) : 쫒아내기 위해서 비교가 필요없음.

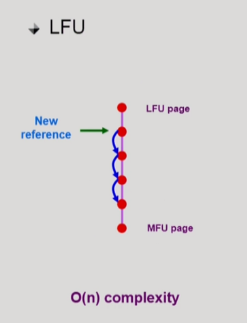
LFU 알고리즘은 적은 한줄로 줄세우기 함.
- 가장 참조 횟수가 적은 page가 위에 있고,
- 가장 참조 횟수가 많은 page가 아래에 있음.
- 사실 한줄로 줄세우기가 불가능해.
- 참조 횟수가 1이 늘어났다고 해서 제일 밑으로 내려오는게 아니라, 비교해서 어디까지 내려갈 수 있는지 확인해야함.
- 시간 복잡도 O(N)이 되어버림.
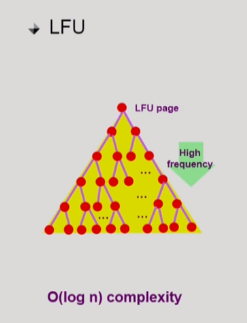
그래서 이런 자료구조를 쓰지 않고, heap이라는 자료구조를 이용해서 구현함.
- 시간 복잡도 O(log n) 가능.
- 이진트리
-
자식이 두개씩 있는 이진트리
-
맨위에는 참조횟수가 제일 적은 page
-
밑으로 갈수록 참조횟수가 많은 page임.
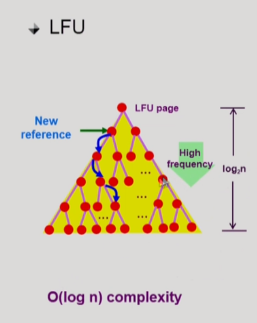
-
자식 둘과만 비교해서 만약 내가 참조횟수가 많으면 자리를 변경한다.
-
전체가 n개라고 라면, 높이가 log 2의 N이 된다.
- 그래서 비교횟수가 많아봐야 log N이 됨.
n이 100만이라고 하면,
log 2의 100만이라고 하면, 값이 10~20 숫자
-
다양한 캐슁 환경

