문제 설명
n개의 송전탑이 전선을 통해 하나의 트리 형태로 연결되어 있습니다. 당신은 이 전선들 중 하나를 끊어서 현재의 전력망 네트워크를 2개로 분할하려고 합니다. 이때, 두 전력망이 갖게 되는 송전탑의 개수를 최대한 비슷하게 맞추고자 합니다.
송전탑의 개수 n, 그리고 전선 정보 wires가 매개변수로 주어집니다. 전선들 중 하나를 끊어서 송전탑 개수가 가능한 비슷하도록 두 전력망으로 나누었을 때, 두 전력망이 가지고 있는 송전탑 개수의 차이(절대값)를 return 하도록 solution 함수를 완성해주세요.
제한사항
n은 2 이상 100 이하인 자연수입니다.wires는 길이가 n-1인 정수형 2차원 배열입니다.wires의 각 원소는[v1, v2]2개의 자연수로 이루어져 있으며, 이는 전력망의v1번 송전탑과v2번 송전탑이 전선으로 연결되어 있다는 것을 의미합니다.- 1 ≤ v1 < v2 ≤ n 입니다.
- 전력망 네트워크가 하나의 트리 형태가 아닌 경우는 입력으로 주어지지 않습니다.
입출력 예
| n | wires | result |
|---|---|---|
| 9 | [[1,3],[2,3],[3,4],[4,5],[4,6],[4,7],[7,8],[7,9]] | 3 |
| 4 | [[1,2],[2,3],[3,4]] | 0 |
| 7 | [[1,2],[2,7],[3,7],[3,4],[4,5],[6,7]] | 1 |
입출력 예 설명
입출력 예 #1
다음 그림은 주어진 입력을 해결하는 방법 중 하나를 나타낸 것입니다.
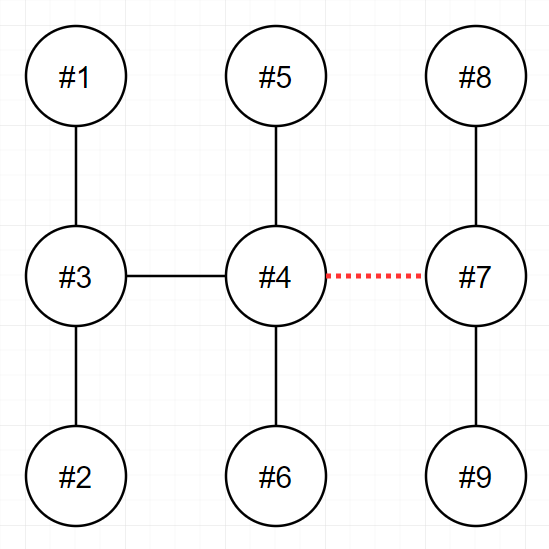
4번과 7번을 연결하는 전선을 끊으면 두 전력망은 각 6개와 3개의 송전탑을 가지며, 이보다 더 비슷한 개수로 전력망을 나눌 수 없습니다.
또 다른 방법으로는 3번과 4번을 연결하는 전선을 끊어도 최선의 정답을 도출할 수 있습니다.
입출력 예 #2
다음 그림은 주어진 입력을 해결하는 방법을 나타낸 것입니다.

2번과 3번을 연결하는 전선을 끊으면 두 전력망이 모두 2개의 송전탑을 가지게 되며, 이 방법이 최선입니다.
입출력 예 #3
다음 그림은 주어진 입력을 해결하는 방법을 나타낸 것입니다.
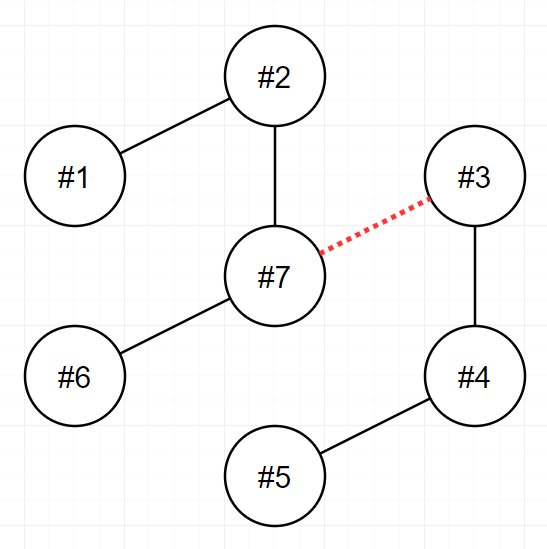
3번과 7번을 연결하는 전선을 끊으면 두 전력망이 각각 4개와 3개의 송전탑을 가지게 되며, 이 방법이 최선입니다.
풀이
1. 테스트 통과 실패 케이스
간선을 가장 많이 갖고있는 노드 사이를 끊는 방법
| wires | n | result |
|---|---|---|
| [[2, 1], [3, 1], [1, 4], [4, 5], [5, 6], [7, 6], [8, 6]] | 8 | 0 |
해당 케이스의 경우 실패한다.
import statistics
from collections import Counter
def failed_solution(n, wires):
answer = []
array = sum(wires, [])
counter = {k: v for k, v in dict(Counter(array)).items() if v == 1}
max_arr = []
min_arr = list(counter.keys())
_max = statistics.mode(array)
for i in range(len(wires)):
if _max in wires[i]:
if not (wires[i][0] and wires[i][1] in min_arr):
max_arr.append(i)
for m in max_arr:
cnt = len(wires[:m]) - len(wires[m + 1 :])
answer.append(abs(cnt))
return min(answer)2. BFS(너비 우선 탐색)를 이용한 방식
from collections import deque
def bfs(graph, i, visit, connect):
queue = deque([i])
visit[i] = True
cnt = 1
while queue:
q = queue.popleft()
for g in graph[q]:
if not visit[g] and connect[i][g]:
queue.append(g)
visit[g] = True
cnt += 1
return cnt
3. DFS(깊이 우선 탐색)를 이용한 방식
def dfs(graph, i, visit, connect):
cnt = 1
visit[i] = True
for v in graph[i]:
if not visit[v] and connect[i][v]:
cnt += dfs(graph, v, visit, connect)
return cnt
그래프를 돌면서 전력망을 하나씩 끊는 방식
- 전력망 끊기
DFS또는BFS로 양쪽 네트워크의 수를 구한 후 해당 값의 차이- 전력망 연결
끊은 간선의 양끝부터 시작해서 도착했을때 송전탑의 갯수를 구하는 방법.
| DFS(깊이우선탐색) | BFS(너비우선탐색) |
|---|---|
| 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색 | 현재 정점에 연결된 가까운 점들부터 탐색 |
| 경로의 특징 | 최단거리 |
| 스택, 재귀함수 | 큐 |
4. 최종 풀이
def solution(n, wires):
answer = float("inf")
connect = [[True] * (n + 1) for _ in range(n + 1)]
graph = [[] for _ in range(n + 1)]
for start, end in wires:
graph[start].append(end)
graph[end].append(start)
for start, end in wires:
visit = [False] * (n + 1)
connect[start][end] = False
count_s = dfs(graph, start, visit, connect)
count_e = dfs(graph, end, visit, connect)
# count_s = bfs(graph, start, visit, connect)
# count_e = bfs(graph, end, visit, connect)
connect[start][end] = True
answer = min(answer, abs(count_s - count_e))
return answer
n = 9
wires = [[1, 3], [2, 3], [3, 4], [4, 5], [4, 6], [4, 7], [7, 8], [7, 9]]
# result : 3
n = 4
wires = [[1, 2], [2, 3], [3, 4]]
# result :0
n = 7
wires = [[1, 2], [2, 7], [3, 7], [3, 4], [4, 5], [6, 7]]
# result :1
print(solution(n, wires))
