[JS] 정렬 알고리즘 정리

홍건우·2023년 4월 1일
JavaScript알고리즘
0

정렬 알고리즘은 데이터를 특정한 기준에 따라 정렬하는 알고리즘으로 정렬 알고리즘은 데이터 처리에서 매우 중요한 역할을 한다.
이번 글에서는 가장 많이 사용되고 또 헷갈릴 수 있는 정렬 알고리즘들에 대해 정리해보며 JavaScript 구현 코드까지 같이 작성해봤다.

선택 정렬(Selection Sort)

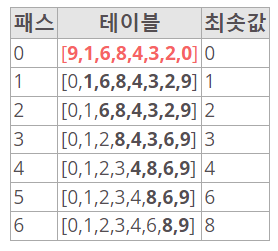
  • 선택 정렬은 주어진 리스트에서 최소값을 찾아 맨 앞에 위치한 값과 교체하고, 그 다음 최소값을 찾아 두 번째 위치한 값과 교체하는 방식으로 정렬하는 알고리즘이다.
  • 선택 정렬 알고리즘의 시간 복잡도는 O(n^2)이다.

선택 정렬1

선택 정렬2

선택 정렬 코드(JS)

function selectionSort(array) {
  for (let i = 0; i < array.length - 1; i++) {
    let minIndex = i;
    for (let j = i + 1; j < array.length; j++) {
      if (array[j] < array[minIndex]) {
        minIndex = j;
      }
    }
    if (minIndex !== i) {
      [array[i], array[minIndex]] = [array[minIndex], array[i]];
    }
  }
  return array;
}

arr = [4, 5, 3, 1, 2, 8, 7, 6];
arr = selectionSort(arr);
console.log(arr); // [1, 2, 3, 4, 5, 6, 7, 8]

삽입 정렬(Insertion Sort)

  • 삽입 정렬은 가장 간단한 정렬 방식으로, 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교 하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다.
  • 두 번째 키와 첫 번째 키를 비교해 순서대로 나열(1회 전)하고, 이어서 세 번째 키를 첫 번째, 두 번째 키와 비교해 순서대로 나열(2회전)하고, 계속해서 n번째 키를 앞의 n-1개의 키와 비교하여 알맞은 순서에 삽입하여 정렬하는 방식이다.
  • 일반적으로 선택 정렬에 비해 실행 시간 측면에서 더 효율적인 알고리즘으로 알려져 있다. (데이터가 거의 정렬 되어 있을 때는 퀵 정렬보다 더 효율적이다.)
  • 삽입 정렬 알고리즘의 시간 복잡도는 O(n^2), 최선의 경우 O(n).

삽입 정렬

삽입 정렬 코드(JS)

function insertionSort(array) {
  for (let i = 1; i < array.length; i++) {
    for (let j = i; j > 0; j--) {
      if (array[j] < array[j - 1]) {
        [array[j], array[j - 1]] = [array[j - 1], array[j]];
      } else {
        break;
      }
    }
  }
  return array;
}

arr = [4, 5, 3, 1, 2, 8, 7, 6];
arr = insertionSort(arr);
console.log(arr); // [1, 2, 3, 4, 5, 6, 7, 8]

퀵 정렬(Quick Sort)

  • 퀵 정렬 알고리즘은 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법 중 하나로, 분할 정복(divide and conquer) 방식을 이용하여 데이터를 정렬하는 알고리즘이다.
  • 리스트에서 하나의 원소를 선택하여 이를 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 분할하고 이후 왼쪽과 오른쪽 리스트를 각각 다시 퀵 정렬 알고리즘을 이용하여 정렬한다.
  • 퀵 정렬의 평균 시간 복잡도는 O(nlogn), 최악의 경우 O(n^2) ⇒ 이미 데이터가 정렬되어 있는 경우 매우 느리게 동작한다.(삽입 정렬과 반대된다.)

정렬 과정

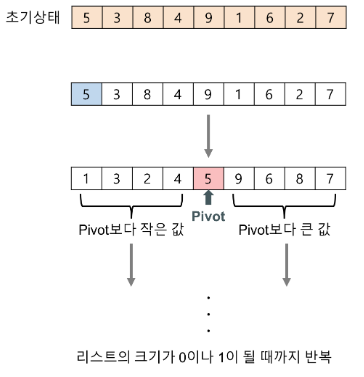
  1. 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
  2. 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
  3. 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
  • 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
  • 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
  1. 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
  • 리스트의 크기가 0이나 1이 될 때까지 반복한다.

퀵 정렬 과정

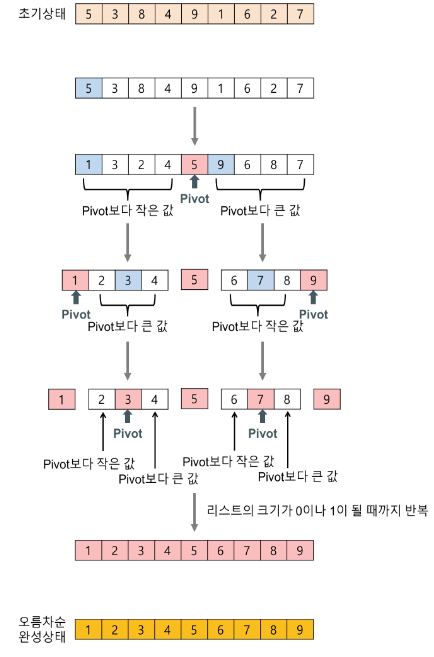
상세 과정

  • 분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
  • 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
  • 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
    순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

퀵 정렬 상세 과정

피벗을 정하는 기준?

피벗의 값은 임의의 값으로 해도 상관은 없다.
보통은 리스트에서 첫 번째 데이터를 피벗으로 정한다.(호어 분할, Hoare Partition)

퀵 정렬 코드(JS)

function quickSort(arr) {
  if (arr.length <= 1) return arr;

  const pivot = arr[0]; //피벗을 리스트의 첫 번째 데이터로 정한다.
  const left = [];
  const right = [];

  for (let i = 1; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }

  const sortedLeft = quickSort(left);
  const sortedRight = quickSort(right);

  return [...sortedLeft, pivot, ...sortedRight];
}

const arr = [4, 5, 3, 1, 2, 8, 7, 6];
const sortedArr = quickSort(arr);
console.log(sortedArr); // [1, 2, 3, 4, 5, 6, 7, 8]

계수 정렬

  • 특정한 조건이 부합할 때만 사용할 수 있는 알고리즘으로 매우 빠른 정렬 알고리즘이다.
  • 모든 데이터가 양의 정수인 상황에서 데이터의 개수가 N, 데이터 중 최댓값이 K일 때 최악의 경우에도 O(N + K)를 보장한다.
  • 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때만 사용할 수 있다. ⇒ 계수 정렬을 이용할때 모든 범위를 담을 수 있는 크기의 배열을 사용하기 때문이다.
    (ex. 모든 원소의 값이 0보다 크거나 같다고 가정했을때, 가장 큰 데이터가 1,000이라면 1,001개의 데이터(0 ~ 1,000)가 들어갈 수 있는 배열이 필요하다.
  • 계수 정렬은 상황에 따라서 심각한 비효율성을 보여줄 수 있는데, 데이터가 0과 999,999 단 2개만 존재한다고 가정하면 그래도 배열의 크기가 100만 개가 되도록 새로운 배열을 선언해줘야한다.

    즉 계수 정렬은 데이터의 크기가 한정되어 있고, 데이터의 크기가 많이 중복되어 있을수록 유리하며 항상 사용할 수는 없기 때문에 데이터의 특성을 파악할 수 없다면 퀵정렬을 이용하는 것이 편리하다.

계수 정렬 과정

  1. [4, 5, 1, 3, 2, 0]라는 배열을 계수 정렬한다고 가정했을때 [0, 0, 0, 0, 0, 0]으로 초기화된 새로운 배열을 만든다.

    012345
    000000

  2. 배열을 순회하며 각 숫자가 몇 번 나왔는지 계수 배열에 기록한다.
    [4, 5, 1, 3, 2, 0]

    012345
    0개0개0개0개1개0개

    [4, 5, 1, 3, 2, 0]

    012345
    0개0개0개0개1개1개

    [4, 5, 1, 3, 2, 0]

    012345
    0개1개0개0개1개1개

    [4, 5, 1, 3, 2, 0]

    012345
    0개1개0개1개1개1개

    [4, 5, 1, 3, 2, 0]

    012345
    0개1개1개1개1개1개

    [4, 5, 1, 3, 2, 0]

    012345
    1개1개1개1개1개1개

  3. 배열을 순회하며 각 숫자가 몇 개씩 등장했는지 확인하여 새로운 배열(정렬된 배열)을 생성한다.

따라서, 계수 정렬의 결과는 [0, 1, 2, 3, 4, 5]이다.

계수 정렬 JS 코드

function countingSort(arr) {
  const count = new Array(Math.max(...arr) + 1).fill(0); //최댓값 + 1의 크기만큼 배열 생성
  const result = [];

  for (let i = 0; i < arr.length; i++) {
    count[arr[i]]++;
  }

  for (let i = 0; i < count.length; i++) {
    for (let j = 0; j < count[i]; j++) {
      result.push(i);
    }
  }

  return result;
}

// 모든 원소의 값이 0보다 크거나 같다고 가정한다.
const arr = [4, 5, 1, 3, 2, 0];
const sortedArr = countingSort(arr);
console.log(sortedArr); // [0, 1, 2, 3, 4, 5]

버블 정렬(Bubble Sort)

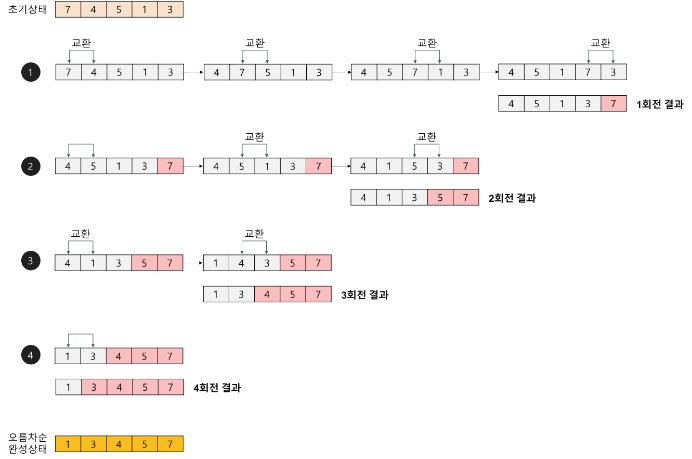
  • 버블 정렬은 인접한 두 개의 데이터를 비교하여 크기가 작은 데이터를 앞으로, 큰 데이터를 뒤로 이동시키는 방식으로 정렬하는 알고리즘이다.
  • 첫 번째 데이터와 두 번째 데이터를, 두 번째 데이터와 세 번째 데이터를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 데이터를 비교하여 교환하면서 데이터를 정렬한다.
    1회전을 수행하고 나면 가장 큰 데이터가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 데이터는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 데이터까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
  • 버블 정렬의 시간 복잡도는 O(n^2)

버블정렬1

버블정렬2

힙 정렬(Heap Sort)

힙 정렬은 완전 이진 트리를 기반으로 하는 정렬 방법이다. 최대 힙/최소 힙을 구성해 정렬을 수행한다.

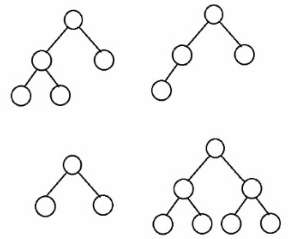
완전 이진 트리

완전 이진 트리는 트리의 노드가 왼쪽에서 오른쪽으로 채워지는 이진 트리로, 마지막 레벨을 제외한 모든 레벨이 꽉 찬 상태인 이진 트리를 말한다. 왼쪽부터 순서대로 노드가 채워지며 이러한 특징은 배열로 구현할 때 인덱스 계산이 용이하다는 장점이 있다.

완전이진트리 예시

힙(Heap)

  • 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
  • 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
  • 힙은 일종의 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
    • 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
    • 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.
  • 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)

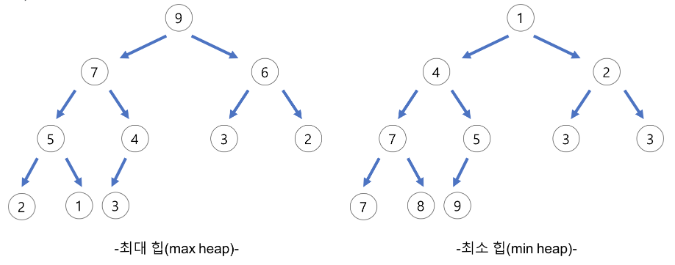
최대 힙 & 최소 힙

  • 최대 힙(max heap)
    • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
    • key(부모 노드) >= key(자식 노드)
  • 최소 힙(min heap)
    • 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
    • key(부모 노드) <= key(자식 노드)

최대 힙 & 최소 힙

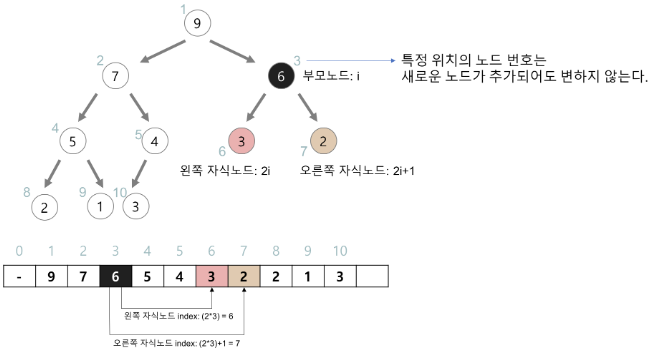
힙 구현

  • 힙은 보통 배열을 사용하여 저장한다.
  • 구현의 편의를 위해 첫 번째 인덱스 0은 사용하지 않는다.
  • 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
    • 예를 들어 루트 노드의 오른쪽 노드의 번호는 항상 3이다.
  • 힙에서의 부모 노드와 자식 노드의 관계
    • 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
    • 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
    • 부모의 인덱스 = (자식의 인덱스) / 2

힙 구현

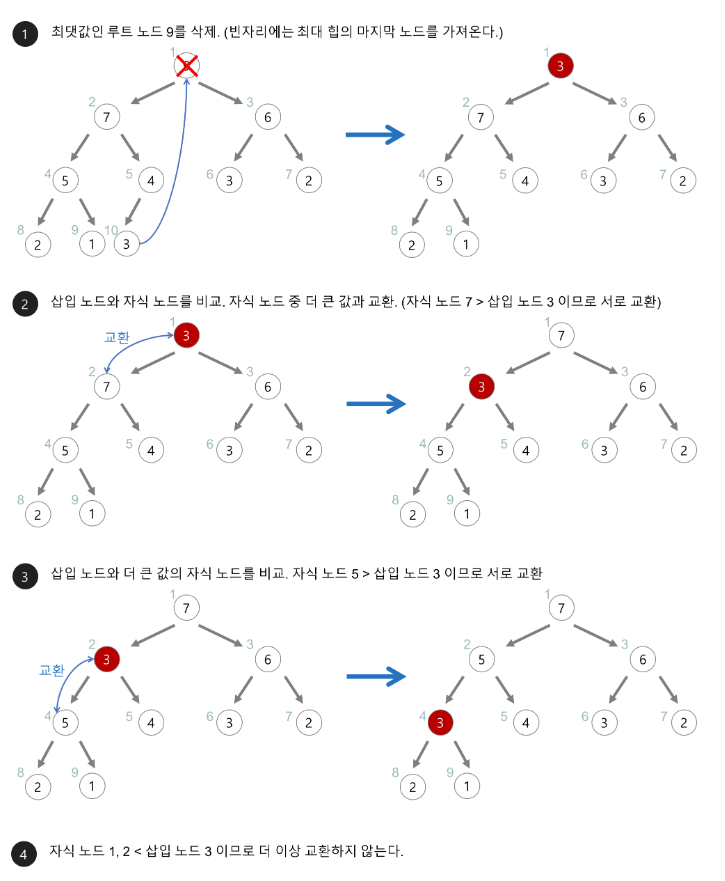
정렬 과정

  1. 주어진 배열을 최대 힙 구조로 바꾼다.
  2. 최대 힙에서 가장 큰 값을 추출해 배열의 마지막에 위치시킨다.
  3. 추출된 값은 힙에서 제거한다.
  4. 남은 힙 구조를 다시 최대 힙 구조로 만든다.
  5. 위 과정을 반복해 정렬을 완성한다.

힙 정렬 과정

최소 힙 정렬 코드(JS)

class MinHeap {
  constructor() {
    this.heap = [ null ]; // 첫 번째 원소는 구현의 편의상 사용하지 않는다.
  }

  size = () => {
    return this.heap.length - 1;
  };

  swap = (a, b) => {
    [this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
  };

  push = (value) => {
    this.heap.push(value);
    let curIdx = this.heap.length - 1; // 새로 삽입한 노드의 index
    let parentIdx = Math.floor(curIdx / 2); // 자식 노드의 부모 노드 인덱스를 구함(자식의 인덱스 / 2)

    while (curIdx > 1 && this.heap[parentIdx] > this.heap[curIdx]) { // 부모 노드의 값이 자식 노드의 값보다 큰 경우 반복
      this.swap(curIdx, parentIdx); //자식노드와 부모노드의 값을 바꿈
      curIdx = parentIdx; // 부모 노드의 인덱스를 자식 노드 인덱스로 대입
      parentIdx = Math.floor(curIdx / 2); // 새로운 자식 노드의 부모 노드 인덱스를 구함
    }
  };

  pop = () => {
    if (this.heap.length === 2) return this.heap.pop();

    const result = this.heap[1]; // 배열 첫 원소(idx 0)은 비워두므로 root는 heap[1]에 위치
    this.heap[1] = this.heap.pop(); 
    let curIdx = 1;
    let leftIdx = curIdx * 2; //왼쪽 자식의 인덱스 = 부모 인덱스 * 2
    let rightIdx = curIdx * 2 + 1; // 오른쪽 자식의 인덱스 = (부모 인덱스 * 2) + 1

    if (!this.heap[leftIdx]) return result; // 왼쪽 자식이 없음은 오른쪽 자식도 없다는 것이므로 바로 반환
    if (!this.heap[rightIdx]) {
      if (this.heap[leftIdx] < this.heap[curIdx]) { // 오른족 자식은 없지만 왼쪽 자식이 있는 경우
        this.swap(leftIdx, curIdx);
      }
      return result;
    }
    
    while (this.heap[leftIdx] < this.heap[curIdx] || this.heap[rightIdx] < this.heap[curIdx]) {
      const minIdx = this.heap[leftIdx] > this.heap[rightIdx] ? rightIdx : leftIdx;
      this.swap(minIdx, curIdx);
      curIdx = minIdx;
      leftIdx = curIdx * 2;
      rightIdx = curIdx * 2 + 1;
    }
    return result;
  };
}

시간 복잡도

  • 힙 구조를 구성하는 시간 복잡도: O(nlogn)
  • 정렬을 수행하는 시간 복잡도: O(nlogn)
  • 최악의 경우에도 O(nlogn)의 시간 복잡도를 가진다는 것이 보장된다.

병합(합병) 정렬(Merge Sort)

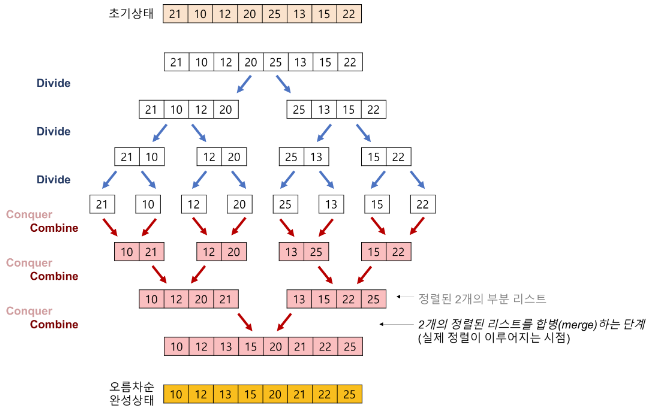
병합 정렬 알고리즘은 분할 정복(divide and conquer) 방식을 이용하여 데이터를 정렬하는 알고리즘으로, 리스트를 두 개의 균등한 크기로 분할하고, 각각 정렬을 수행한 후, 분할된 리스트를 병합하여 전체 리스트를 정렬한다.

예시

  1. [6, 5, 3, 1, 8, 7, 2, 4] 가 있다고 가정하자.
  2. 하나의 배열을 두 개로 쪼갠다.
    [6, 5, 3, 1] [8, 7, 2, 4]
  3. 두 개의 배열을 네 개로 쪼갠다.
    [6, 5] [3, 1] [8, 7] [2, 4]
  4. 네 개의 배열을 여덟 개로 쪼갠다.
    [6] [5] [3] [1] [8] [7] [2] [4]
  5. 더 이상 쪼갤 수가 없으니 두 개씩 합치기를 시작한다. 합칠 때는 작은 숫자가 앞에 큰 숫자를 뒤에 위치시킨다.
    [5, 6] [1, 3] [7, 8] [2, 4]
  6. 이제 4개의 배열을 2개로 합친다. 각 배열 내에서 가장 작은 값 2개를 비교해서 더 작은 값을 먼저 선택하면 자연스럽게 크기 순으로 선택된다.
    [1, 3, 5, 6] [2, 4, 7, 8]
  7. 최종적으로 2개의 배열도 마찬가지로 크기 순으로 선택하가면서 하나로 합치면 정렬된 배열을 얻을 수 있다.
    [1, 2, 3, 4, 5, 6, 7, 8]

병합 정렬 예시

병합 정렬 예시

시간 복잡도

병합 정렬의 시간 복잡도는 O(nlogn)이다.

이는 리스트를 분할하여 정렬하는 데 logn의 시간이 걸리고, 분할된 리스트를 병합하는 데 n의 시간이 걸리기 때문이다. 이러한 특성 때문에 대부분의 경우 퀵 정렬보다 느리지만 입력값이 큰 경우에는 퀵 정렬보다 유리할 수 있다.

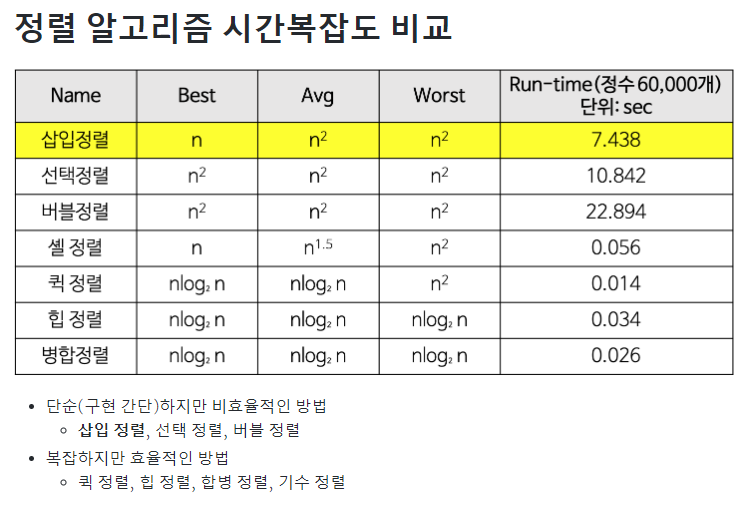
각 정렬 알고리즘 시간 복잡도 정리

정렬 알고리즘 시간 복잡도 정리

profile
홍건우
컴퓨터공학과 학생입니다
이전 포스트

[JS] 조합과 순열

다음 포스트

[JS] +0과 -0

0개의 댓글