재귀란?

자기 자신을 호출하는 것

예시) 피보나치

int fibo(int n) {
if n <=1 return 1;
return fibo(n-1) + fibo(n-2);
}

n번째 항을 구하는데 중복해서 계산되는 항이 발생해서 O(1.618^n)의 시간이 걸린다

DP로 해결하면 중복해서 계산되는 게 없다.
계산결과를 배열로 저장하면 된다.

int fibo(int n) {
  int f[20]; //배열 만드릭
  f[0] = f[1] = 1;
  for(int i = 2; i <= n; i++)
    f[i] = f[i-1] + f[i+2];
  return f[n];
}

N+1번째 칸을 채우면 O(N)에 답을 알 수 있다.
이렇게 중간값을 저장하느냐에 따라 시간 차이가 난다.

DP를 구하는 과정

1. 테이블 정의하기
2. 점화식 찾기
3. 초기값 정하기

코딩테스트에 나오는 DP 유형 풀이과정이다.

주어진 문제가 DP로 푸는 것인지 알아차리지 못한다.

BOJ 1463번 : 1로 만들기

문제

정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지이다.
1) X가 3으로 나누어 떨어지면, 3으로 나눈다.
2) X가 2로 나누어 떨어지면, 2로 나눈다.
3) 1을 뺀다.
정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

• 입력
  첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
• 출력
  첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.

나는 일단 딱 봤을 때 풀이 방법이 바로 안 떠오르면 굳이 더 생각하지 않고 바로 풀이방식을 보고 익힌다. 떠오를 말락 할 때만 조금 더 생각해본다.

풀이

1. 테이블 정하기

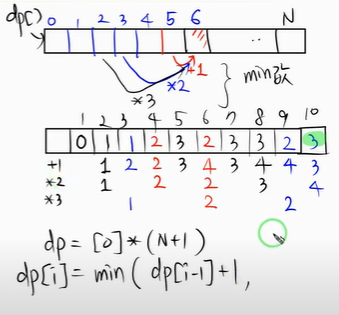
D[i] = i를 1로 만들기 위해 필요한 연산 사용 횟수의 최솟값

2. 점화식 찾기

D[12]=?
D[12] = 1이 되려면?
D[1]부터 D[11]까지의 값을 다 알고 있다고 해보자.
그러니까, 1,2,...,11을 1로 만들기 위한 최소 횟수를 다 알고 있다.
3으로 나눔 => D[12] = D[4] + 1
2로 나눔 => D[12] = D[6] + 1
1을 뺌 => D[12] = D[11] + 1
--> D[12] = min(D[4] + 1, D[6] + 1, D[11] + 1)

D[k] =?
3으로 나누어 떨어지면 3으로 나누거나(D[k] = D[k/3] + 1)
2로 나누어 떨어지면 2로 나누거나(D[k] = D[k/2] + 1)
1을 빼거나(D[k] = D[k-1] + 1), 이들 중에서 최솟값

3. 초기값 정하기

D[1] = 0

코드

N = int(input())

# DP 테이블 초기화
D = [0] * 1000001

D[1] = 0
# DP진행
for i in range(2, N+1): #D[1]=0
	D[i] = D[i-1] + 1
    if i%2 == 0 :
    	D[i] = min(D[i], D[i//2] + 1)
    if i%3 == 0 :
    	D[i] = min(D[i], D[i//3] + 1)
 
print(D[N])  

위 코드는 bottom-up 방식이다.
모든 배열을 다 채워 원하는 값을 구하는 방식이다.

BOJ 9095번 : 1, 2, 3 더하기

문제

정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.

1+1+1+1
1+1+2
1+2+1
2+1+1
2+2
1+3
3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.

• 입력
  첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.

• 출력
  각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.

풀이

D = [0] * 12
D[1:4] = [1, 2, 4]
for i in range(4, 12):
	D[i] = sum(D[i-3:i])

T = int(input())
for _ in range(T):
	N = int(input())
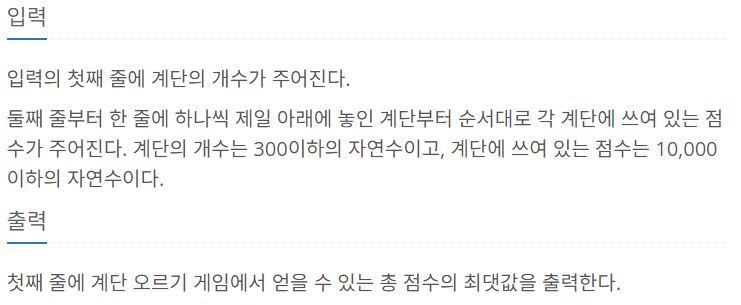
    print(D[N])

BOJ 2579번 : 계단 오르기

풀이

1. 테이블 정의하기
   D[i] = i번째 계단까지 올라섰을 때 점수 합의 최댓값

2. 점화식 찾기
   D[1] = 10, D[2] = 20, D[3] = 35

-> 연속된 세 개의 계단을 밟으면 안된다는 제약조건을 D[i]로 구현할 수 있는 점화식은 없다.

N = int(input())
stairs = [0]*(N+1)
for i in range(1, N+1):
	stairs[i] = int(input())

D = [0] * (N+1)
for i in range(4, N+1):
	D[i] =


print(D[N])

Reference

• [바킹독의 실전 알고리즘] 0x10강 다이나믹 프로그래밍
• 문어박사 IT편의점 [백준문제집 DP 필수문제] (백준, 파이썬)