출처: 파이썬으로 그래프 구현하기
*️⃣그래프란?
도시와 도시 사이를 연결하는 도로나 컴퓨터 네트워크 또는 사람의 인맥 관계처럼 어떤 관계(relationships)를 표현하는 수학 구조를 그래프라고 한다.
도시, 컴퓨터, 사람 등을 노드(node 또는 vertex)라 하고, 이들을 연결하는 도로, 네트워크, 인맥 등을 간선(edges)이라 한다.
그래프는 노드의 집합과 간선의 집합으로 구성된다. 이것을 수학으로 표현하면 아래와 같다.
- : 노드의 집합
- : 두 노드를 연결하는 간선(edges)의 집합
- 노드 와 를 연결하는 간선을 라고 하면, 이다.
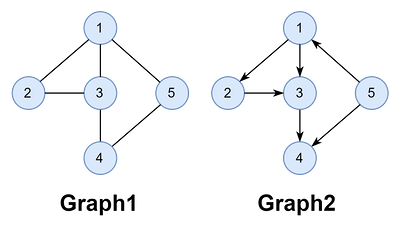
예를 들어 아래 그림과 같은 그래프를 라고 하면, 와 는 다음과 같다.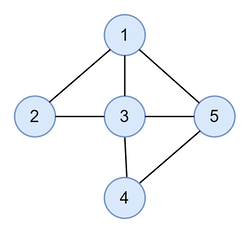
- =
{1, 2, 3, 4, 5} - =
{(1, 2), (1, 3), (1, 5), (2, 3), (3, 4), (3, 5), (4, 5)}
그래프의 종류
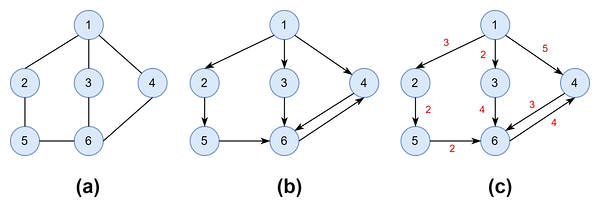
- 무방향 그래프(undirected graph)
- 위 그림의 (a)처럼 두 노드를 연결하는 간선에 방향이 없는 그래프
- 위 그림의 (a)처럼 두 노드를 연결하는 간선에 방향이 없는 그래프
- 방향 그래프(directed graph)
- 그림 (b)처럼 간선에 방향이 있는 그래프(방향 그래프의 간선은 < >로 표기한다.)
- 그림 (b)처럼 간선에 방향이 있는 그래프(방향 그래프의 간선은 < >로 표기한다.)
- 가중 그래프(weighted graph)
- 그림 (c)처럼 노드를 연결하는 간선에 가중치(weight)를 부여한 그래프다. 따라서 간선을 로 표현한다. 이때 그래프는 무방향 그래프일 수도 있고, 방향 그래프일 수도 있다.
- 가중치는 한 지점에서 다른 지점으로 이동하는 데 필요한 비용이나 걸리는 시간 등으로 이해하자.
파이썬으로 그래프 표현하기
앞서 그래프를 관계(relationships)를 표현하는 자료구조라고 했다. 파이썬에서 어떤 관계를 표현할 때 적합한 것은 사전(dictionary)이다. 
- 키(key): 노드
- 값(value): 키와 연결된 노드 리스트
#무방향 그래프
graph1 = {1: [2, 3, 5], 2: [1, 3], 3: [1, 2, 4], 4: [3, 5], 5: [1, 4]}
#방향 그래프
graph2 = {1: [2, 3], 2: [3], 3: [4], 4: [], 5: [1, 4]}인접 리스트로 표현하기
리스트의 인덱스 = 딕셔너리의 키(key)#무방향 그래프 graph1 = [[], [2, 3, 5], [1, 3], [1, 2, 4], [3, 5], [1, 4]] #방향 그래프 graph2 = [[], [2, 3], [3], [4], [], [1, 4]]여기서는 인덱스와 노드의 값을 맞추기 위해 인덱스
0에 빈 리스트를 넣었다.
*️⃣DFS
그래프를 "깊이" 우선 탐색하기
이진 트리에서 전위 순회할 때, 부모를 먼저 방문한 후에 왼쪽과 오른쪽 자식을 방문한 것과 거의 같은 방식이다.
이진 트리는 부모에서 자식으로 가는 방향이 있고, 모든 노드가 루트 노드에 연결된 그래프에 해당한다. 하지만 그래프는 방향이 없을 수도 있고, 모든 노드가 특정 노드에 모두 연결되는 것이 아니란 점을 고려하여 탐색한다.
앞서 예로 든 아래 그림의 무방향 그래프를 노드 1부터 깊이 우선 탐색하는 과정을 간단히 정리한다.
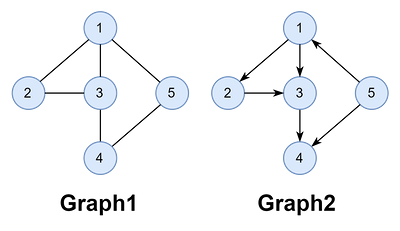
- 노드
1을 방문 처리한다. - 노드
1에 연결된 노드[2, 3, 5]중에서 아직 방문하지 않은 한 곳을 방문한다.
먼저 노드 2를 방문해 보자. - 그리고 노드
2에 연결된 노드[1, 3]중에서 노드1을 이미 방문했으므로, 아직 방문하지 않은 노드3을 방문한다.- 즉, 다음 방문할 노드가 이미 방문한 노드인지 확인해야 한다.
- 여기서는
visited라는 집합을 만들고, 방문한 노드를visited에 추가한다. - 그리고 어떤 노드를 방문할 때마다
visited에 있는 노드인지 확인한다.
- 노드
3에 연결된 노드[1, 2, 4]중에서 아직 방문하지 않은 노드4를 방문한다. - 같은 방식으로 노드
5를 방문한다. - 모든 노드를 방문했으므로 종료한다.
Recursive DFS
재귀적으로 깊이 우선 탐색하기
graph1 = {1: [2, 3, 5], 2: [1, 3], 3: [1, 2, 4], 4: [3, 5], 5: [1, 4]} #무방향 그래프
graph2 = {1: [2, 3], 2: [3], 3: [4], 4: [], 5: [1, 4]} #방향 그래프
def dfs_recursive(graph, node):
#방문 결과를 담을 리스트와 방문 여부를 확인할 집합을 만든다.
res = []
visited = set()
#깊이 우선 탐색하는 재귀함수를 만든다.
def _dfs(u):
# 이미 방문한 노드이면 종료한다.
if u in visited:
return
#현재 노드를 방문 처리한다.
#즉, 방문 결과 리스트와 방문 여부를 확인할 집합에 추가한다.
visited.add(u)
res.append(u)
#현재 노드와 간선으로 연결된 노드들을 깊이 우선 탐색한다.
for v in graph[u]:
_dfs(v)
_dfs(node)
return res
print("무방향 그래프의 깊이 우선 탐색")
print("==========================")
print("노드 1에서 시작: ", dfs_recursive(graph1, 1))
print("노드 2에서 시작: ", dfs_recursive(graph1, 2))
print()
print("방향 그래프의 깊이 우선 탐색")
print("========================")
print("노드 1에서 시작: ", dfs_recursive(graph2, 1))
print("노드 2에서 시작: ", dfs_recursive(graph2, 2))위의 코드를 실행한 결과는 아래와 같다.
무방향 그래프의 깊이 우선 탐색
==========================
노드 1에서 시작: [1, 2, 3, 4, 5]
노드 2에서 시작: [2, 1, 3, 4, 5]
방향 그래프의 깊이 우선 탐색
========================
노드 1에서 시작: [1, 2, 3, 4]
노드 2에서 시작: [2, 3, 4]방향 그래프를 노드 1에서 탐색을 시작하면 노드 5에 갈 수 있는 길이 없으므로, 결과가 [1, 2, 3, 4]이다.
인접 리스트로 표현한 DFS
graph1 = [[], [2, 3, 5], [1, 3], [1, 2, 4], [3, 5], [1, 4]] #무방향 그래프 graph2 = [[], [2, 3], [3], [4], [], [1, 4]] #방향 그래프 def dfs_recursive(graph, node): #이하 코드는 위의 코드와 완전히 같다.실행해 보면 같은 결과가 나온다.
스택을 이용한 DFS
def dfs(graph, node):
#방문할 노드를 저장한 스택과 방문 여부를 확인한 집합을 만든다.
#스택과 집합에 방문할 첫 노드를 넣는다.
res = []
stack = [node]
visited = set(stack)
#스택이 빌 때까지 반복한다.
while stack:
#스택에서 노드를 꺼내고 방문처리한다.
u = stack.pop()
res.append(u)
#현재 노드에 연결된 다른 노드를 확인한다.
#다른 노드가 아직 방문하지 앟는 노드이면, 스택과 집합에 넣는다.
for v in graph[u]:
if v not in visited:
visited.add(v)
stack.append(v)
return res
print("무방향 그래프의 깊이 우선 탐색")
print("==========================")
print("노드 1에서 시작: ", dfs(graph1, 1))
print("노드 2에서 시작: ", dfs(graph1, 2))
print()
print("방향 그래프의 깊이 우선 탐색")
print("========================")
print("노드 1에서 시작: ", dfs(graph2, 1))
print("노드 2에서 시작: ", dfs(graph2, 2))위의 코드를 실행한 결과는 아래와 같다.
무방향 그래프의 깊이 우선 탐색
==========================
노드 1에서 시작: [1, 5, 4, 3, 2]
노드 2에서 시작: [2, 3, 4, 5, 1]
방향 그래프의 깊이 우선 탐색
========================
노드 1에서 시작: [1, 3, 4, 2]
노드 2에서 시작: [2, 3, 4]방문 결과의 순서를 보면, 재귀적으로 구현한 것과 다르다. 스택은 후입선출이라서 나중에 들어간 노드가 먼저 방문 결과에 들어가기 때문에 나오는 결과다.
무방향 그래프의 탐색 과정을 짧게 살펴보자.
- 첫 노드
1을 방문한 후에 노드1에 연결된 노드[2, 3, 5]를 순서대로 스택에 넣는다. - 그리고 스택에서 노드를 꺼내면 노드
5가 먼저 나온다. - 따라서 방문 결과가
[1, 5 ...]순이다.
*️⃣BFS
그래프를 "너비" 우선 탐색하기
c.f) 너비 우선 탐색은 이진 트리의 레벨 순서 순회와 같다.
무방향 그래프를 노드 1부터 너비 우선 탐색해 보자. 너비 우선 탐색은 큐를 사용한다.
- 노드
1을 방문처리하고, 큐에 넣는다. - 큐에서 노드
1을 꺼내서 출력한다. - 노드
1에 인접한 노드2, 3, 5를 방문처리하고 큐에 넣는다. - 큐에서 노드
2를 꺼내서 출력한다. 노드2에 인접한1과3을 방문했으므로 큐에서 노드를 꺼낸다. - 위의 과정을 반복한다.
- 그러면 1, 2 ,3, 5, 4순으로 출력된다.
처리 과정을 보면 스택을 이용한 깊이 우선 탐색과 비슷하다. 스택 대신 큐를 사용한 점만 다르다.
graph1 = {1: [2, 3, 5], 2: [1, 3], 3: [1, 2, 4], 4: [3, 5], 5: [1, 4]} #무방향 그래프
graph2 = {1: [2, 3], 2: [3], 3: [4], 4: [], 5: [1, 4]} #방향 그래프
def bfs(graph, node):
res = []
queue = [node]
visited = set(queue)
while queue:
u = queue.pop(0)
res.append(u)
for v in graph[u]:
if v not in visited:
visited.add(v)
queue.append(v)
return res
print("무방향 그래프의 너비 우선 탐색")
print("==========================")
print("노드 1에서 시작: ", bfs(graph1, 1))
print("노드 2에서 시작: ", bfs(graph1, 2))
print()
print("방향 그래프의 너비 우선 탐색")
print("========================")
print("노드 1에서 시작: ", bfs(graph2, 1))
print("노드 2에서 시작: ", bfs(graph2, 2))위의 코드를 실행한 결과는 아래와 같다.
무방향 그래프의 너비 우선 탐색
==========================
노드 1에서 시작: [1, 2, 3, 5, 4]
노드 2에서 시작: [2, 1, 3, 5, 4]
방향 그래프의 너비 우선 탐색
========================
노드 1에서 시작: [1, 2, 3, 4]
노드 2에서 시작: [2, 3, 4][그림] 무방향 그래프의 너비 우선 탐색 (노드 1에서 시작)

인접 리스트로 표현한 BFS
앞서 인접 리스트로 표현한 그래프도 위의 함수를 그대로 사용하여 너비 우선 탐색할 수 있다.graph1 = [[], [2, 3, 5], [1, 3], [1, 2, 4], [3, 5], [1, 4]] #무방향 그래프 graph2 = [[], [2, 3], [3], [4], [], [1, 4]] #방향 그래프 def bfs(graph, node): #이하 코드는 위의 코드와 완전히 같다.실행하면 같은 결과가 나온다.
*️⃣다익스트라(Dijkstra) 알고리즘
가중 그래프에서 최단 경로 찾기
앞서 공부한 너비 우선 탐색으로 찾은 경로는 중간 노드의 개수가 최소이지만, 최단 경로는 아니다. 다익스트라 알고리즘은 가중 그래프에서 최단 경로(Shortest Path)를 찾는다. 네비게이션으로 길 찾는 예를 든다면 최소 시간 또는 최소 거리 경로를 찾는 알고리즘이 다익스트라 알고리즘이다.
위성 항법 시스템(Global Navigation Satellite System)을 이용하여 길 찾을 때도 다익스트라 알고리즘을 이용한다고 한다.
다익스트라 알고리즘의 기본 개념은 최단 경로는 여러 개의 최단 경로로 이루어진다는 것이다. 가중 그래프를 보자.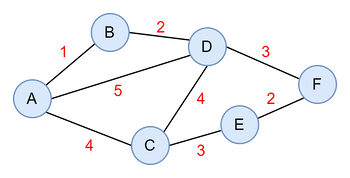
graph = {
"A": [("B", 1), ("C", 4), ("D", 5)],
"B": [("A", 1), ("D", 2)],
"C": [("A", 4), ("D", 4), ("E", 3)],
"D": [("A", 5), ("B", 2), ("C", 4), ("F", 3)],
"E": [("C", 3), ("F", 2)],
"F": [("D", 3), ("E", 2)]
}
이 그래프의 최소 경유지(환승) 경로는 A → D → F이지만,
최단 경로(최소 시간 경로)는 A → B → D → F이다.
이것을 구간별로 나눠보자.
- A에서 D까지 가는 최단 경로는 A → B →D이다.
- A에서 B까지 가는 최단 경로는 A → B이다.
- 즉, 구간별로 쪼개서 봐도 모두 최단 경로다.
이번에서 B에서 E로 가는 최단 경로를 살펴보자.
- 최단 경로는 B → D → F → E이다
- B에서 F까지 가는 최단 경로는 B → D → F이다.
- B에서 D까지 가는 최단 경로는 B → D이다.
즉, 너비 우선 탐색을 하면서 각 경로로 가는 소요 시간을 기록해 두고, 소요 시간을 비교하여 시간이 적게 걸리는 경로를 먼저 탐색하는 것이 다익스트라 알고리즘의 원리다.
너비 우선 탐색에서는 큐를 사용하여, 큐에 집어넣는 순서대로 경로를 탐색한다. 그러나, 다익스트라 알고리즘은 큐에 집어넣은 순서에 상관없이 가중치가 작은 것을 먼저 꺼내서 탐색하는 것이 핵심이다.
손으로 풀어보기
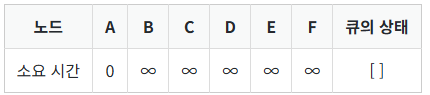
- 먼저 각 노드에 도달하는 데, 걸리는 시간을 최댓값으로 초기화하고 출발 노드의 소요 시간을 "0"으로 만든다. 노드 A를 방문한다.
- A에 인접한 노드 B, C, D까지 가는 소요 시간이나 거리(가중치)를 계산하고, 기존 소요 시간과 비교하여 갱신한다. 이때 소요 시간이 갱신되는 노드를 큐에 넣는다.
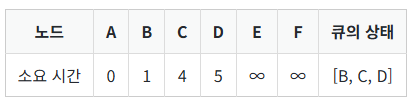
- 큐에서 소요 시간이 가장 적은 노드 B를 꺼내고, 방문 처리한다.
- B에 인접한 노드 중 A는 이미 방문했으므로, D까지 가는 경로만 갱신한다.
- 현재 A에서 D까지 가는 소요 시간은 5이다. 그런데 A에서 B를 거쳐서 D로 가면 A → B의 소요 시간 1과 B → D의 소요 시간 2를 더한 3이다.
- 따라서 D까지 가는 소요 시간을 3으로 갱신한다. 그리고 큐에 넣는다.

- 큐에서 소요 시간이 가장 적은 노드 D를 꺼내고, 방문 처리한다.
- D에 인접한 노드 중 A, B는 방문했으므로 노드 C와 F에 대해 소요 시간을 계산하여 갱신한다.
- C는 D를 거쳐서 가는 것보다 A에서 바로 갈 때 시간이 적게 걸리므로 그냥 둔다.
- F는 D까지 오는데 걸리는 최소 시간 3과 D에서 F로 가는 데 걸리는 시간 3을 더하여 6으로 갱신한다.
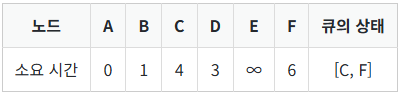
- 위의 과정을 반복하여 소요 시간을 기록한 결과는 다음과 같다.
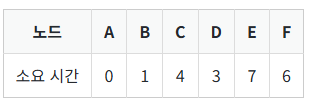 위의 표를 보면 노드 A에서 출발했을 때 각 노드까지 가는데 걸리는 최소 시간이 기록되어 있다. 최단 경로는 앞서 너비 우선 탐색으로 찾은 경로를 복원하는 것과 같은 방법으로 복원한다.
위의 표를 보면 노드 A에서 출발했을 때 각 노드까지 가는데 걸리는 최소 시간이 기록되어 있다. 최단 경로는 앞서 너비 우선 탐색으로 찾은 경로를 복원하는 것과 같은 방법으로 복원한다.
파이썬으로 구현하기
구현할 때 고려할 점
- 노드
A에서 출발했을 때 각 노드까지 가는데 걸리는 최소 시간이 기록하기 - 너비 우선 탐색과 비슷하게 진행되지만, 큐 대신 우선순위에 따라 꺼내는 자료 구조를 사용해야 한다.
- 지금까지 공부한 자료 구조 중에서, 이 조건을 만족하는 것은 최소 힙이다. 공부하다 보니 우선순위 큐라는 자료 구조를 구현하는 방법 중 하나가 힙이라고 한다.
- 여기서는 파이썬의
heapq모듈을 이용한다. - 힙에서 꺼낼 때 최소 시간순으로 꺼내야 하므로, 힙에 넣을 자료는
(소요 시간, 노드)다.
- 방문 처리하는 순서에 유의한다.
- 앞서 만든
bfs와 달리 heap에서 꺼낸 후에 방문 처리한다.
- 앞서 만든
- 각 노드에 도달하는 데 걸리는 시간을 계산하고 비교하여, 시간을 갱신할 때만 힙에 넣는다.
#소요 시간을 초기화할 때 사용할 무한대(inf)를 이용하기 위해 수학 모듈 사용
import math
import heapq
graph = {
"A": [("B", 1), ("C", 4), ("D", 5)],
"B": [("A", 1), ("D", 2)],
"C": [("A", 4), ("D", 4), ("E", 3)],
"D": [("A", 5), ("B", 2), ("C", 4), ("F", 3)],
"E": [("C", 3), ("F", 2)],
"F": [("D", 3), ("E", 2)]
}
def dijkstra(graph, node):
#소요시간을 기록할 사전과 현재 노드의 이전 노드를 기록할 사전을 초기화
lead_time = {node: math.inf for node in graph}
node_from = {node: None for node in graph}
#출발 노드(node)의 소요 시간을 0으로 만든다.
lead_time[node] = 0
visited = set()
#(소요 시간, 노드)의 자료를 넣는 최소 힙을 만든다.
#그리고 출발 노드를 힙에 넣는다.
heap = []
heapq.heappush(heap, (0, node))
#힙이 빌 때까지 반복한다.
while heap:
#힙에서 자료를 꺼내서 시간과 노드를 변수에 저장한다.
prev_time, u = heapq.heappop(heap)
#이미 방문한 노드이면 다음 노드를 꺼내고, 그렇지 않으면 방문처리한다.
if u in visited:
continue
visited.add(u)
#현재 노드에 인접한 노드와 가중치(소요 시간)를 가져와서 반복한다.
for v, weight in graph[u]:
#인접한 노드로 가는 소요 시간을 계산하여 기본 값보다 작으면,
#시간 정보를 갱신하고, 이전 노드를 기록한다. 그리고 힙에 넣는다.
if (new_time := prev_time + weight) < lead_time[v]:
lead_time[v] = new_time
node_from[v] = u
heapq.heappush(heap, (lead_time[v], v))
#소요 시간과 이전 노드를 기록한 사전을 반환한다.
return lead_time, node_from
lead_time, node_from = dijkstra(graph, "A")
print("A에서 다익스트라 탐색 후의 node_from과 lead_time의 상태")
print(node_from)
print(lead_time)실행 결과는 다음과 같다.
A에서 다익스트라 탐색 후의 node_from과 lead_time의 상태
{'A': None, 'B': 'A', 'C': 'A', 'D': 'B', 'E': 'C', 'F': 'D'}
{'A': 0, 'B': 1, 'C': 4, 'D': 3, 'E': 7, 'F': 6}참고 링크

