• 출처: 바킹독의 실전 알고리즘 강의

1. 목차

2. 난이도 있는 기초

이론적인 내용

• 시간 & 공간 복잡도
  실질적인 필요성: 코딩 테스트 문제는 시간 제한과 메모리 제한이 주어진다.

• 시간 복잡도

• 컴퓨터가 1초에 할 수 있는 연산의 수 3-5억개
  연산이 비트, AND, OR, 비교, 덧셈(단순 연산) / 나눗셈, 곱셈, 대입, 함수 호출(복잡한 연산)
  이냐에 따라 연산의 수는 달라진다.

• 짧은 코드에서 연산이 4번 정도 필요할 경우 >>> 0.00001초도 안 걸릴 것이다.

• 만약 시간 제한이 1초라면, 내 프로그램은 3-5억 번의 연산 안에 수행되어야 한다.

• 인간 컴파일러도 아니고.. 연산이 몇 개 인지 하나하나 뜯어보는 건 심각한 노가다..

• 상수는 떼고, 적당히 n번의 연산이 필요하다. 고상하게는 n에 비례한다고 퉁쳐서 얘기를 한다.

• 입력의 크기와 문제를 해결하는데 걸리는 시간의 상관관계

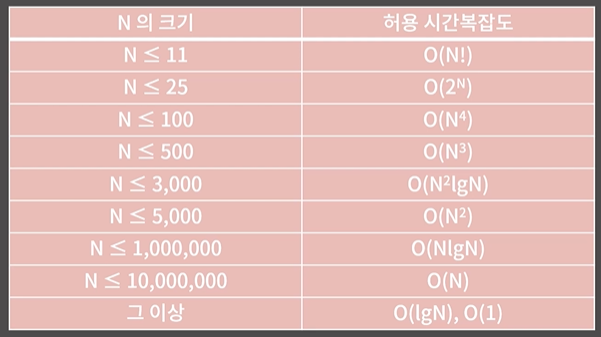
• 알고리즘의 시간복잡도가 시간 제한 내에 ... ...

3. 기초(2)

... ...

4. 자료구조 - 배열

1) 정의와 성질

• 자료구조로서의 배열:

  메모리 상에 원소를 연속하게 배치한 자료구조
  - 길이를 마음대로 늘리거나 줄일 수 있다.

• 자료구조로서의 배열의 성질:

  1) k번째 원소를 찾는 시간복잡도
  = 시작주소에서 k칸만큼 오른쪽으로 이동
  = $O(1)$
  2) 추가적으로 소모되는 메모리의 양(=overhead)가 거의 없음
  3) 메모리 상에 데이터들이 붙어있으므로 Cache hit rate 가 높음
  4) 메모리 상에 연속한 구간을 잡아야 해서 할당에 제약이 걸림
• 2,3,4번 성질은 코딩테스트와 별로 상관이 없다.

2) 기능과 구현

1) 임의의 위치에 있는 원소를 확인하고 변경하는 연산
= $O(1)$
2) 원소를 끝에 추가 - 길이를 1 증가
= $O(1)$
3) 마지막 원소를 제거 - 길이를 1 줄임
= $O(1)$
4) 임의의 위치에 원소를 추가
= $O(N)$
중간에 원소를 추가하게 되면 그 뒤의 원소들은 전부 한 칸씩 밀어야 해서 O(N)이 필요하게 된다.
마치 책장에 책이 연속해서 꽂혀있을 때 중간에 책을 넣기 위해서는 나머지 책들을 밀어야하는 것과 같은 상황이다.
추가하는 위치가 끝에 가까울수록 시간은 줄어들고, 앞에 가까울수록 시간은 늘어날테지만 평균적으로는 N/2개를 밀어야하니 O(N)이라고 해도 상관이 없다.
5) 임의의 위치에 있는 원소를 제거
= $O(N)$
중간에 원소를 지웠다고 치면 그 이후에 있던 모든 원소들을 한 칸씩 땡겨와야해서 그렇다.
그냥 다 내버려두고 그 원소 자리만 비워두면 안되냐고 생각할 수도 있지만
그렇게 되면 더 이상 메모리 상에 원소가 연속해서 존재하지 않기 때문에
배열의 정의에도 위배되고 또 k번째 원소를 O(1)에 찾을 수가 없게 된다.

정리

임의의 위치에 있는 원소를 확인/ 변경 = $O(1)$

list = [10, 20, 30]
list[2] = 500
print(list) # [10, 20, 500]

원소를 끝에 추가 = $O(1)$

list = [10, 20, 30]
list.insert(len(list), 500)
print(list) # [10, 20, 30, 500]

마지막 원소를 제거 = $O(1)$

# 마지막 요소를 삭제하고 반환
list = [10, 20, 30, 20]
list.pop(len(list))
print(list) # [10, 20, 30]

임의의 위치에 원소를 추가/임의 위치의 원소 제거 = $O(N)$

list = [10, 20, 30]
list.insert(len(list), 500)
print(list) # [10, 20, 30, 500]

# 특정 인덱스의 요소를 삭제하고 반환
list = [10, 20, 30, 20]
list.pop(2)
print(list) # [10, 30, 20]

# 특정 값을 찾아서 삭제. 
# 만약 리스트에 같은 값이 여러 개 있을 경우 처음 찾은 값을 삭제
list.remove(20)
print(list) # [10, 30, 20]

->> 파이썬은 함수가 이미 다 있다...

참고 사이트

• Cache hit rate 란?

5. 자료구조 - 연결 리스트

1) 정의와 성질

2) 기능과 구현

3) STL list

4) 연습문제