알고리즘 성능 평가

seon·2024년 1월 3일

알고리즘

Algorithm

목록 보기

2/41

출처 : 이것이 취업을 위한 코딩 테스트다 with 파이썬

복잡도(Complexity)

알고리즘을 성능을 평가하기 위해 복잡도의 개념이 사용된다.

시간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘의 수행 시간 분석
공간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘의 메모리 사용량 분석

동일한 기능을 수행하는 알고리즘이 있다면, 일반적으로 복잡도가 낮을수록 좋은 알고리즘입니다.

단순히 소스코드가 복잡하게 보인다와는 다른 개념입니다.

대걔 소스코드가 길고 모듈이 많은 경우 알아보기가 어려우니까 코드가 복잡하다 이런식으로 말을 하곤 하는데요, 그러한 상황에서 단순히 코드가 보기 복잡하다 아니면 이해하기에 복잡하다와는 다른 의미라고 보시면 되겠습니다.

여기서 복잡도는, 그 특정한 함수의 성능적인 측면에서의 복잡도를 의미하는 것입니다.

다시 말해서

시간복잡도가 높다고 하는 것은 수행시간 측면에서 더 많은 시간이 소요될 수 있다는 것을 의미합니다.
시간 복잡도가 낮다는 것은 해당 알고리즘이 더 빠르게 수행될 수 있다는 것을 나타낸 것이죠.
공간복잡도가 높다는 것은 많은 메모리가 필요할 수 있다는 의미가 되는 것입니다.

기능이 동일하다고 한다면 복잡도가 낮을 수록 좋은 알고리즘이다.

빅오 표기법(Big-O Notation)

복잡도는 어떠한 방식으로 표기할 수 있을까요?

빅오 표기법

가장 빠르게 증가하는 항만을 고려하는 표기법

함수의 상한만을 나타내게 됩니다.

사실 빅오 표기법도 엄밀한 의미를 이해하기 위해서는
'계산 복잡도 이론'에 대해서 더욱 자세하게 찾아보아야 되는데요
다만 일반적으로 알고리즘 문제를 푸는 입장에서는
빅오 표기법이란 가장 빠르게 증가하는 항만을 고려하는구나 정도만 기억하셔도 문제의 요구사항을 분석하는 데에는 큰 어려움이 없습니다.

예를 들어 연산횟수가 $3n^3+5n^2+1,000,000$ 인 알고리즘이 있다고 하자.
- 빅오 표기법에서는 차수가 가장 큰 항만 남기므로 $O(n^3)$ 으로 표현됩니다.
이제 빅오 표기법의 개념은 극한의 개념으로 생각해 보시면 더욱더 쉽게 이해할 수 있는데요,
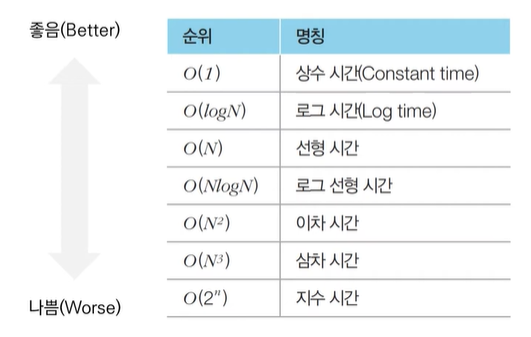
상수 시간, 로그 시간, 선형 시간(linear time),
로그 선형 시간, 이차 시간, 삼차 시간 etc.
많이 사용하는 말이므로 기억해둡니다.

시간 복잡도 계산해보기

예제 (1)

array = [3, 5, 1, 2, 4] # 5개의 데이터(N = 5)
summary = 0 # 합계를 저장할 변수

# 모든 데이터를 하나씩 확인하며 합계를 계산
for x in array:
	summary += x

# 결과를 출력
print(summary)

N 개의 데이터가 존재할 때 그 데이터를 모두 더한 값을 구하는 프로그램의 예제이다.

[] 는 리스트 객체를 나타낸다.

summary는 0으로 초기화

모든 데이터를 하나씩 확인하면서 그 값을 summary에 더해줍니다.

마지막으로 결과를 출력하는 것을 확인할 수 있는데요

수행 시간은 데이터의 개수 N에 비례할 것임을 예측할 수 있습니다.
- 시간 복잡도 : $O(N)$
모든 데이터를 하나씩 확인하며 합계를 계산하기 때문.
총 데이터의 개수만큼 summary 변수에 값이 더해지겠죠.
summary 값에 0을 대입하거나, summary 값을 출력하거나 이런 식으로 다양한 명령어들이 사용된 걸 확인할 수 있어요,
다만 이제 N이 커짐에 따라서 영향을 받는 부분은 바로 모든 데이터를 하나씩 확인하며 합계를 구하는 부분이라 할 수 있겠죠.
- 그렇기 때문에 N값이 증가함에 따라서 바로(for문) 이 부분이 영향을 받게 되고, 데이터의 개수 N이 많이 커지게 되면 사실 이 부분을 제외한 다른 부분은 사실상 없는 것과 마찬가지로 전체 프로그램의 성능에 많은 영향을 미치지는 않을 것입니다.

예제 (2)

array = [3, 5, 1, 2, 4] # 5개의 데이터(N=5)

for i in array:
	for j in array:
    	temp = i * j
        print(temp)

시간 복잡도 : $O(N^2)$

참고로 모든 2중 반복문의 시간 복잡도가 $O(N^2)$ 인 것은 아닙니다.

소스코드가 내부적으로 다른 함수를 호출한다면 그 함수의 시간 복잡도까지 고려해야 합니다.

알고리즘 설계 Tip

Python <-> PyPy
- 이 중 한쪽으로 제출했을 때 시간초과 또는 메모리 초과가 발생하는 경우 동일한 코드를 다른 한쪽으로 제출하면 된다.
$N>=5,000$ 이라면 천2백50억 이 그 연산 횟수라고 볼 수 있는데요,
파이썬이 1초에 약 5천만번 정도의 계산을 처리할 수 있다고 하면, 약 2500초 정도가 걸린다고 말할 수 있겠네요.
실제로 채점용 서버에서는, 파이썬이 1초에 2천만번 정도의 연산만 처리할 수 있다고 가정하고 문제에 접하자.
이 또한 채점용 서버의 컴퓨터 성능에 따라서 천차만별일 수 있기 때문에 이점 또한 유의하여 실제 문제를 푸시는 것을 추천드립니다.
수행 시간 제한은 통상 1초~5초 이다.
시간 제한이 명시되어 있지 않은 경우 대략 5초 정도라고 생각을 하시고 문제를 풀자.

요구사항에 따라 적절한 알고리즘 설계하기

하지만 외관적으로 봤을 때 시간 복잡도가 낮아 보이더라도 다른 요인에 의해서 불필요하게 시간이 많이 소요되서 시간 초과 판정을 받는 경우도 있고
굉장히 다양한 케이스가 존재할 수 있기 때문에
이렇게 시간 제한에 따라서 적절한 알고리즘을 설계하는 것은 많은 문제를 접해 보면서
스스로 감을 찾아나가기!

알고리즘 문제 해결 과정

문제를 처음 접했을 때,
나는 이 문제를 엄청 간결하고 창의적으로 풀 수 있다고 스스로한테 확신을 가지시고
문제를 푸시는 게 결과적으로 실수를 줄이고 더욱 빠르게 여러분들의 실력을 늘려줄 수 있을 겁니다.

수행 시간 측정 소스코드 예제

일반적인 알고리즘 문제 해결 과정은 다음고 같습니다.

import time # 표준 라이브러리에서 time을 불러온다.
start_time = time.time() # 측정 시작

# 프로그램 소스코드
end_time = time.time() # 측정 종로
print("time:", end_time - start_time) # 수행 시간 출력