[leet code] 2467. Most Profitable Path in a Tree

[leet code] 2467. Most Profitable Path in a Tree

🗒️알고리즘 분류

#valid tree #tree #dfs #backtracking #트리 #재귀 #백트래킹

📌기억할 만한 포인트

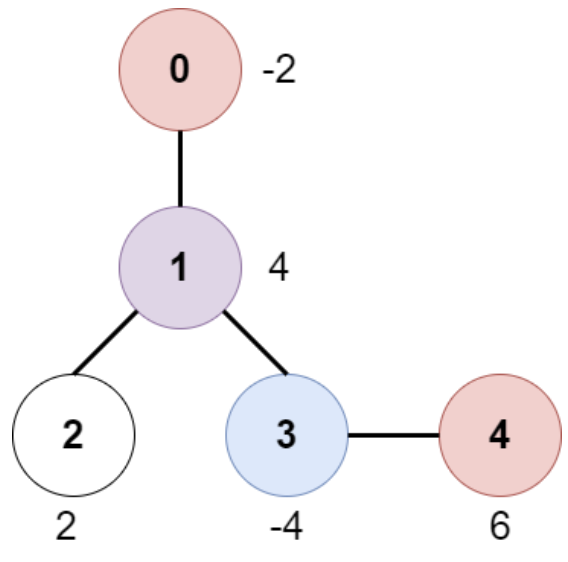
Alice, Bob 이 각각의 주어진 노드에서 출발하여, 각 노드에 담긴 amount 를 갖는다. Alice 는 항상 0번 노드에서 출발하여 leaf node 에 도착하면 이동을 멈추고, Bob 은 주어진 노드에서 출발하여 0번 노드에 도착하면 멈춘다.

Alice 가 노드에 도달하면 해당 노드의 amount 를 온전히 가질 수 있고, Bob 과 동시에 도달하면 해당 노드의 amount 를 반만 가질 수 있으며 Bob 이 먼저 도달한 다음 Alice 가 도달하면 Alice 는 아무것도 갖지 못한다.

이때 Alice 가 가질 수 있는 amount 의 최댓값을 구하는 문제이다.

dfs, backtracking 문제이다.

기억할 만한 점은 총 2가지이다.

1. dfs 를 총 2번 실행해야 한다.
   • 먼저 Bob 의 시작 노드 부터 0번 노드까지 최단 경로를 알아야 한다. Map 또는 int[] 배열 등을 사용하여 Bob 의 최단경로(BobPath)를 알아야 한다. BobPath 에는 Bob이 0번 노드로 가는 경로 상에서 각 노드에 도달하는 "시간(깊이)"를 저장한다. (backtracking)
   • BobPath 를 알아냈다면 이제 AliceIncome 의 최댓값을 알아내면 된다. 각각의 노드에 방문 표시를 하고,
     1. Bob이 해당 노드를 방문하지 않았거나, Alice가 더 빨리 도착하면 전액 획득
     2. 동시에 도착하면 절반만 획득
2. 리프 노드의 조건: Graph.get(cur).size() == 1

Valid Tree 에서의 최단 거리를 구하는 것을 배운 문제였다.

⏳시간 복잡도, 공간 복잡도

• 시간 복잡도: O(N)
• 공간 복잡도: O(N)

📝풀이 코드(JAVA)

import java.util.*;

class Solution {
    private static int AliceIncome = 0;
    private static boolean[] AliceVisited, BobVisited;
    private static Map<Integer, Integer> BobPath;
    private static ArrayList<ArrayList<Integer>> Graph;

    public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
        AliceIncome = Integer.MIN_VALUE; 
        AliceVisited = new boolean[amount.length];
        BobVisited = new boolean[amount.length];
        BobPath = new HashMap<>();
        Graph = new ArrayList<>();

        for (int i = 0; i < amount.length; ++i) {
            Graph.add(new ArrayList<>());
        }

        for (int[] edge : edges) {
            Graph.get(edge[0]).add(edge[1]);
            Graph.get(edge[1]).add(edge[0]);
        }

        dfsBob(bob, 0);
        dfsAlice(0, 0, 0, amount);

        return AliceIncome;
    }

    private void dfsBob(int bob, int depth) {
        BobPath.put(bob, depth);

        if (bob == 0) {
            return;
        }

        BobVisited[bob] = true;
    
        for (int next : Graph.get(bob)) {
            if (BobVisited[next]) continue;
        
            dfsBob(next, depth + 1);
            if (BobPath.containsKey(0)) {
                return;
            }
        }   
    
        BobPath.remove(bob);
    }

    private void dfsAlice(int alice, int aliceVisitedTime, int income, int[] amount) {
        AliceVisited[alice] = true;

        if (!BobPath.containsKey(alice) || aliceVisitedTime < BobPath.get(alice)) {
            income += amount[alice];
        } else if (aliceVisitedTime == BobPath.get(alice)){
            income += amount[alice] / 2;
        }

        if (Graph.get(alice).size() == 1 && alice != 0) {
            AliceIncome = Math.max(AliceIncome, income);
        }

        for (int next : Graph.get(alice)) {
            if (AliceVisited[next]) continue;
            dfsAlice(next, aliceVisitedTime+1, income, amount);
        }
    }
}

⏰총 풀이시간

• 144분;;