1. 문제 설명
- BST의 루트가 주어졌을 때, 트리의 두 개의 다른 노드의 값들 사이의 최소 절대 차이를 반환합니다.
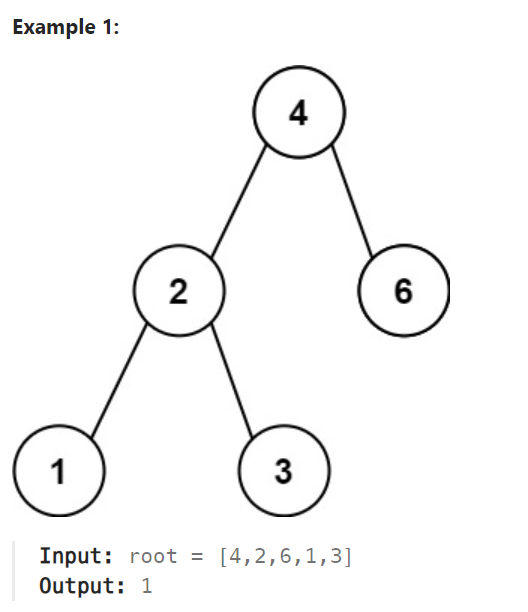
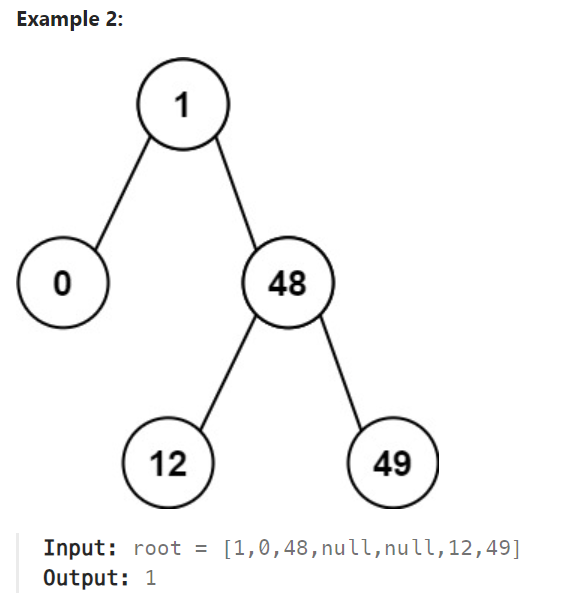
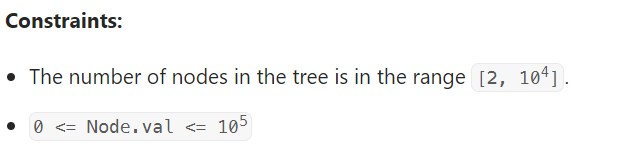
2. 접근 방법
1) [실패] 전역변수 + PreOrder_DFS
- 코드 설명 : root 노드부터 DFS 전위 탐색을 하며 부모 노드 값을 좌우 자식 노드들의 값을 비교하여 절대차를 구하고 가장 작은 절대차를 저장하여 최소 절대차를 구할 수 있다고 생각하여 코드를 작성하였습니다.
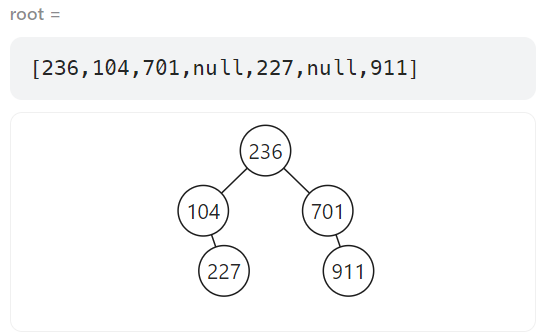
- 실패 원인 : 아래의 테스트 케이스를 예시로 왼쪽 자식 노드는 부모 노드와 가장 적은 차를 가진 관계지만 오른쪽 자식 노드는 root노드와 값이 가장 가깝기 때문에 부모노드와 오른쪽 자식 노드를 비교하면 값의 차이가 많이 나는 에러가 있었습니다. 역시 테스트 케이스에서 너무 잘 넘어가고 빨리 풀린다고 생각했는데.. 문제가 있는 코드였습니다.
class Solution {
int min = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
preOrderDfs(root);
return min;
}
public void preOrderDfs(TreeNode node){
if(node == null)
return;
if(node.left != null && min > node.val - node.left.val)
min = node.val - node.left.val;
if(node.right != null && min > node.right.val - node.val)
min = node.right.val - node.val;
preOrderDfs(node.left);
preOrderDfs(node.right);
}
}
2) [성공😊] InOrder_DFS
- 위의 실패 사례를 생각하여 접근 방식을 바꾸어 접근하였습니다.
- 우선 먼저 이진 검색 트리는 노드의 왼쪽 하위 트리에 노드의 값보다 작은 값들만 있고, 오른쪽 하위 트리에는 노드의 값보다 큰 값들만 있는 트리입니다.
- 이를 중위 탐색을 하면 트리 데이터를 오름차순으로 탐색이 가능하는 점을 고려하여 중위 탐색을 통해 list에 데이터를 오름차순으로 저장하였습니다.
- 오름차순으로 정렬되어 있는 list를 반복문으로 순회하며 앞뒤의 두 값을 연산하여 최소 절대차을 저장하도록 합니다.
- 위 반복문을 통해 얻은 최소 절대차를 반환합니다.
3. 구현 코드
import java.util.*;
class Solution {
List<Integer> list;
public int getMinimumDifference(TreeNode root) {
list = new ArrayList<>();
inOrderDfs(root);
int min = Integer.MAX_VALUE;
for(int i = 0; i < list.size() - 1; i++){
min = Math.min(min, list.get(i+1) - list.get(i));
}
return min;
}
public void inOrderDfs(TreeNode node){
if(node != null){
inOrderDfs(node.left);
list.add(node.val);
inOrderDfs(node.right);
}
}
}
- 시간 복잡도 : O(n)
- 공간 복잡도 : O(n)
4. 개선 사항
- 이전 코드 : 모든 데이터를 조회하며 저장 후 다시 정렬된 모든 데이터를 조회하며 원하는 데이터를 추출했습니다.
- 개선 코드 : 모든 데이터를 조회하며 바로 원하는 데이터를 추출하도록 하여 속도와 메모리 개선을 하였습니다.
- 이전 코드는 DFS 전위 순회로 List에 데이터를 오름차순으로 저장하고 반복 순회를 통해 데이터를 비교하여 결과값을 얻었습니다.
- 하지만 전체 검색을 두번하게 되는 중복 작업이 있어 데이터를 바로 비교하여 원하는 결과값을 얻도록 하였습니다.
- 이를 위해 이전 코드에서 조금만 수정을 해주면 되는데,
int min변수와 최소 절대치를 계산하기 위해 비교할 이전 데이터 TreeNode preNode를 전역변수로 선어하였습니다.
- 그리고 이 변수를 사용하여 DFS 전위 탐색을 하며 바로 최소 절대치를 계산하여
min에 저장하였습니다.
class Solution {
int min = Integer.MAX_VALUE;
TreeNode preNode = null;
public int getMinimumDifference(TreeNode root) {
inOrderDfs(root);
return min;
}
public void inOrderDfs(TreeNode node){
if(node != null){
inOrderDfs(node.left);
if(preNode != null)
min = Math.min(min, node.val - preNode.val);
preNode = node;
inOrderDfs(node.right);
}
}
}
- 시간 복잡도 : O(n)
- 공간 복잡도 : O(n)
5. 최종 회고
- 이진 검색 트리의 특성에 대해 다시 생각하며 풀어 볼 수 있는 좋은 문제였습니다. 생각할수록 풀면 더 풀수록 재밌어지는 자료구조라고 생각이 들면서 어떻게 더 잘 사용할 수 있을지 고민을 조금 더 해보는 시간이 필요할 것 같습니다.
- 코드 개선을 위해 생각하는데 시간과 에너지가 더 필요하지만 여기서 더 많이 배우게 되는 것 같습니다.







