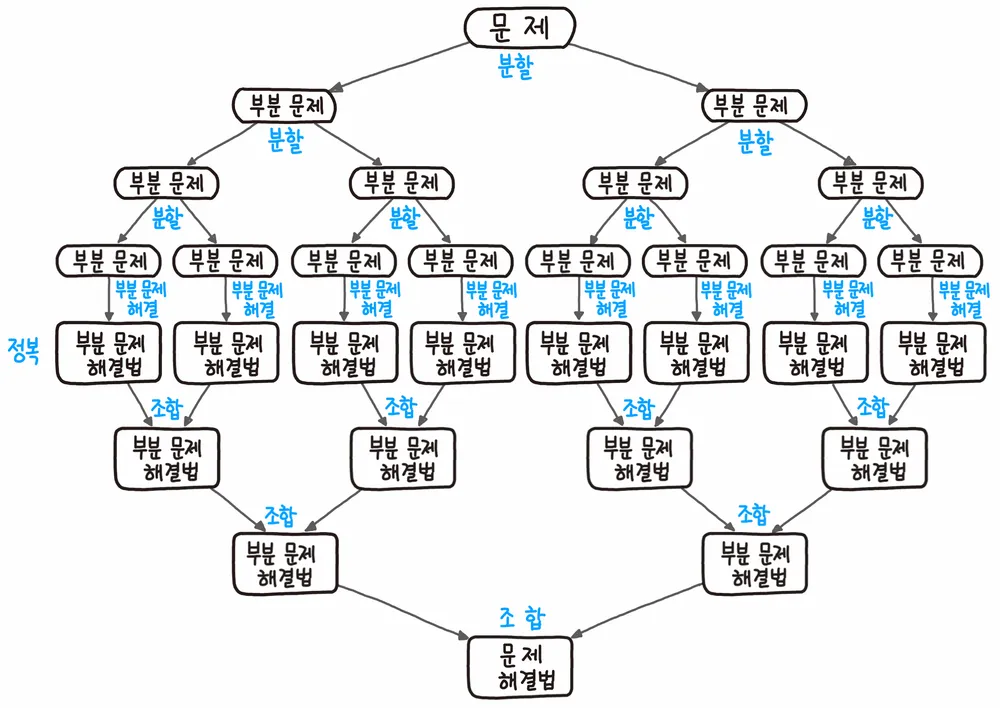
Divide and Conquer (분할 정복)
여러 알고리즘의 기본이 되는 해결방법으로, 기본적으로는 엄청나게 크고 방대한 문제를 조금씩 조금씩 나눠가면서 용이하게 풀 수 있는 문제 단위로 나눈 다음 그것들을 다시 합쳐서 해결하자는 개념이다
- Divide를 제대로 나누면 Conquer과정은 자동으로 쉬워진다. 그래서 Divide를 잘 설계하는 것이 중요하다.
- 분할(Divide)-정복(Conquer)-조합(Combine)의 과정이다.
Divide and Conquer의 특징
- 분할된 작은 문제는 원래 문제와 성격이 동일하다 -> 입력 크기만 작아짐
- 분할된 문제는 서로 독립적이다(중복 제거 X) -> 순환적 분할 및 결과 결합 가능
시간복잡도
분할정복의 시간 복잡도는 각 하위 문제의 크기가 로 줄어들고, 분할되는 문제의 수가 개인 경우(는 분할되는 문제의 수, 는 각 하위 문제의 크기, 는 분할과정을 제외한 각 문제를 해결하는 데 필요한 시간복잡도)
일반적인 빅오 표기법 :
💡 분할 정복의 장점
문제를 나눔으로써 어려운 문제를 해결할 수 있다.
병렬적으로 문제를 해결할 수 있다.
Top-down 재귀방식으로 구현하기 때문에 코드가 직관적이다.
🥺 분할 정복의 단점
함수를 재귀적으로 호출한다는 점에서 함수 호출로 인한 오버헤드가 발생할 수 있다.
스택오버플로우 / 메모리과다사용의 문제가 발생할 수 있다.
📝 분할 정복을 사용하는 문제의 예
- 수열의 빠른 합 fastsum(n) = 2 * fastsum(n/2) + n2/4 (n이 짝수 일때)
- 행렬의 빠른 제곱
- 퀵소트
- 합병정렬
- 고속 푸리에 변환
- 카라추바 알고리즘
🏃 예시 문제 1
해답
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
N, r, c = map(int, input().split())
li = 2**N
def z(n, i, j):
if n == 2 and i <= r < i+n and j <= c < j+n:
if r == i and c == j:
return 1
elif r == i and c == j+1:
return 2
elif r == i+1 and c == j:
return 3
else:
return 4
res = 0
if r < i+n//2 and c < j+n//2:
res += z(n//2, i, j)
elif r < i+n//2 and c < j+n:
res += (n//2) ** 2
res += z(n//2, i, j+n//2)
elif r < i+n and c < j+n//2:
res += ((n//2) ** 2) * 2
res += z(n//2, i+n//2, j)
elif r < i+n and c < j+n:
res += ((n//2) ** 2) * 3
res += z(n//2, i+n//2, j+n//2)
return res
print(z(2**N, 0, 0)-1)🏃 예시 문제 2
해답
🏃 예시 문제 3
<BAEKJOON: 플래티넘 5> 히스토그램에서 가장 큰 직사각형
해답
💯 분할 정복 문제를 더 풀어보고 싶다면?
실버
<BAEKJOON: 실버 3> 쿼드 트리
<BAEKJOON: 실버 3> 특별상이라도 받고 싶어
<BAEKJOON: 실버 1> The Shortest does not Mean the Simplest
골드
<BAEKJOON: 골드 4> 사분면
<BAEKJOON: 골드 2> 박스 채우기
<BAEKJOON: 골드 2> 트리
<BAEKJOON: 골드 1> 트리의 순회