Prefix Sum: 구간 합
부분 합(Partial Sum) 또는 누적 합(Cumulative Sum)이라고도 한다
이름에서 뜻을 추측할 수 있다. 배열이 있는데 그 어느 구간의 합을 구하고 싶을 때 사용하는 알고리즘이다.
일차원적으로 구간 합을 구하는 방식을 생각해보자.
arr = [1, 4, 5, 13, 50, 23, 11, 9, 29, 88]의 길이 10인 배열이 있다. 여기서 index = 3부터 index = 7까지의 구간 합을 구하고 싶다면, index 3부터 7까지 접근하여 13+50+23+11 이렇게 구하면 된다.
그러나 만약 arr가 100,000,000의 길이를 가지고 있으며 그 때 90,000,000의 구간 합을 구하려고 한다면, 9천만 번의 접근이 필요하다는 것이다.
결국 시간복잡도는 구간 합을 구할 때마다 O(N)이 된다.
이를 전처리를 통해 O(1)로 만들기 위해 고안된 알고리즘이 바로 구간 합 알고리즘이다!
📕 Prefix Sum을 사용해야하는 문제의 조건
-
1차원 배열
1차원 배열에서 i부터 j까지의 구간 합을 구하기 위해서는
SUM[i~j] = SUM[j] - SUM[i-1] -
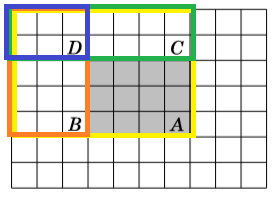
2차원 배열
색칠된 구간의 구간 합 = SUM(A) - SUM(B) - SUM(C) + SUM(D)
💡 Prefix Sum의 장점
구간 합을 구해야 하는 문제에서 빠르게 구할 수 있다!
📝 Prefix Sum을 사용하는 문제의 예
배열의 원소 값이 자주 바뀌지 않는 상황에서 두 번 이상의 구간합 질의가 있는 경우 사용할 수 있다.
c.f. Prefix Sum을 사용하면 안되는 문제의 예
- 구간합을 구해야하는 배열 원소의 값이 자주 바뀌는 경우 -> prefix sum 배열을 자주 업데이트 해주어야 함
- 원소의 값이 자주 바뀐다면 펜윅 트리(=인덱스 트리)나 세그먼트 트리를 사용한다. - 구간합을 한 번 사용하는 경우
🏃 예시 문제 1
<BAEKJOON: 실버 3> 블로그
1차원 배열 구간 합 구하기 예제 문제
해답
누적합을 사용하여, 누적 합 배열 psum을 만들어준 후, 누적합 배열 i번째 값에서 i-X번째 값을 빼주는 것으로 구했다.
import sys
input = sys.stdin.readline
N, X = map(int, input().split())
visit = list(map(int, input().split()))
# 누적 합 사용 > psum[i~j] = psum[i] - psum[j-1]
psum = [0]*(N+1)
# 누적 합 배열 전처리
for i in range(1, N+1):
psum[i] = psum[i-1]+visit[i-1]
# 구하기
if psum[N-1] == 0:
print("SAD")
else:
maximum, cnt = 0, 0
for i in range(X, N+1):
tmp = psum[i]-psum[i-X]
if maximum == tmp:
cnt += 1
elif maximum < tmp:
maximum = tmp
cnt = 1
print(maximum)
print(cnt)🏃 예시문제 2
<BAEKJOON: 실버 1> 주지수
2차원 배열 구간 합 구하기 예제 문제
해답
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
ground = []
for _ in range(N):
ground.append(list(map(int, input().split())))
psum = [[0]*(M+1) for _ in range(N+1)]
for i in range(1, N+1):
for j in range(1, M+1):
if i==0 and j == 0:
psum[i][j] = ground[0][0]
elif i==0:
psum[i][j] = psum[i][j-1]+ground[i-1][j-1]
elif j==0:
psum[i][j] = psum[i-1][j]+ground[i-1][j-1]
else:
psum[i][j] = psum[i-1][j]+psum[i][j-1]-psum[i-1][j-1]+ground[i-1][j-1]
K = int(input())
for _ in range(K):
x1, y1, x2, y2 = map(int, input().split())
print(psum[x2][y2] - psum[x1-1][y2] - psum[x2][y1-1] + psum[x1-1][y1-1])🏃 예시문제 3
해답
💯 Prefix Sum 문제를 더 풀어보고 싶다면?
브론즈
<BAEKJOON: 브론즈 3> 혁
<BAEKJOON: 브론즈 3>
<BAEKJOON: 브론즈 2>
<BAEKJOON: 브론즈 1>
<BAEKJOON: 브론즈 1>
실버
<BAEKJOON: 실버 4>
<BAEKJOON: 실버 4> 0
<BAEKJOON: 실버 2>
<BAEKJOON: 실버 1>
골드
<BAEKJOON: 골드 5>
<BAEKJOON: 골드 4>
<BAEKJOON: 골드 4>
<BAEKJOON: 골드 4>
<BAEKJOON: 골드 2>

