오늘도 백준을 풀다가 새로운 알고리즘 발견..
항상 새로운 알고리즘을 발견할 때마다 정리해두면 좋을 것 같아서 작성하는 글이다.
오늘의 문제 #백준 #1005번 #ACM craft
문제 안에서 게임이름이 ACM Craft (Association of Construction Manager Craft)라고 한다.
건물을 짓는 게임이라 그런가...ㅎㅎ
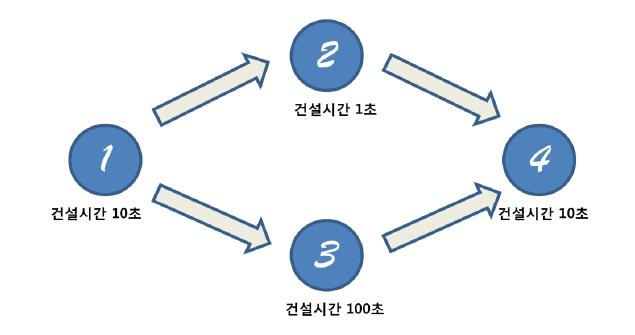
이런 식으로 건물의 건설 순서가 정해지는데,
(위 그림을 보면 1번을 지어야 2,3번을 지을 수 있고.
2,3번을 지어야 4번을 지을 수 있는 이런 식이다)
여기서 주어지는 건물을 짓기 위해 필요한 최소 시간이 얼마냐는 문제이다
이 문제의 분류가 '위상정렬 알고리즘'이다
이 알고리즘을 사용하여 풀어보라는 소리인 듯한데, 일단 초면이기 때문에 알고리즘을 서치해보았다.
아래 추가본 참조..
큐를 이용하는 방법이다.(deque를 사용하겠다)
생각보다 어렵지 않다는 것을 느낄 수 있다
BFS랑 성격이 비슷하다고 느껴진다
필요한 자료구조는 아래와 같이 나열해볼 수 있다.
1. 건물 짓는 순서를 넣어줄 그래프
2. 각 건물마다의 진입 차수
3. 각 건물마다 짓는 데 걸리는 총 시간(기다리는 시간 포함)
결국 ACM craft를 풀었을 때 아래와 같은 코드가 나왔다.
위의 순서를 그대로 설명에 첨부하였으니 이해가 될 것이다.
from collections import deque
def playACM():
N, K = map(int, input().split())
timeToBuild = deque(map(int, input().split())) # 각 빌딩을 짓는 데 드는 시간
timeToBuild.appendleft(0)
graph = [[] for i in range(N+1)]
indegree = [0] * (N+1) # 진입 차수
# 간선 정보 입력받기(선행빌딩)
for _ in range(K):
a, b = map(int, input().split())
graph[a].append(b)
indegree[b] += 1
# 승리를 위해 건설해야하는 건물 번호
W = int(input())
totalTime = [0] * (N+1) # 해당 건물 완성까지 걸리는 총 시간
q = deque() # 큐
# 1. 진입차수가 0인 모든 노드를 큐에 넣는다
# preBuild에서 0인 인덱스 큐에 추가
for i in range(1, N + 1):
if indegree[i] == 0:
q.append(i)
totalTime[i] = timeToBuild[i] # 초기 0인것은 선행 빌딩이 없기 때문에 그대로 넣어줌
# 2. 큐가 빌 때까지 다음 3,4 반복
while q:
# 3. 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거
tmp = q.popleft()
for i in graph[tmp]:
indegree[i] -= 1 # 해당 노드와 연결된 빌딩들의 진입차수에서 -1
# 더 오래 걸리는 시간으로 업데이트
totalTime[i] = max(totalTime[i], totalTime[tmp]+timeToBuild[i])
# 4. 새롭게 진입차수가 0이 된 노드면 큐에 넣음
if indegree[i] == 0:
q.append(i)
print(totalTime[W])
T = int(input())
for _ in range(T):
playACM()위상정렬 알고리즘을 사용하면서, 결국 걸리는 시간을 구해야하는데
현재노드(tmp)에서 다음연결노드(i)로 향할 때마다 시간을 업데이트해주면 된다. 처음에는 그 안쪽 if문에다가 넣었다가 노드 한군데에서만 업데이트해줌을 깨닫고 밖으로 빼왔다.
totalTime[i] = max(totalTime[i], totalTime[tmp]+timeToBuild[i])홧팅
+정리본 추가(2024.02.18)
위상정렬 알고리즘(Topological Sorting Algorithm)
순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용하는 알고리즘
= 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'
= 비순환 방향 그래프(DAG)에서 정점을 선형으로 정렬하는 것Topological Sorting의 특징
정렬 알고리즘의 일종이다시간복잡도
: 차례대로 모든 노드()를 확인하면서 해당 노드에서 출발하는 간선()을 차례대로 제거해야 하기에용어 정리
진입 차수(indegree) : 특정 노드로 '들어오는' 간선의 개수
📕 Topological Sorting을 사용해야하는 문제의 조건
- 비순환 유향 그래프(Directed Acyclic Graph) : 사이클이 없는 방향 그래프
📝 Topological Sorting을 사용하는 문제의 예
- 선수과목을 고려한 학습 순서 설정
🎁 구현 방법
구현하는 방법에는 두 가지가 있다.
-
in_degree를 사용하는 BFS(Breath First Search) 방법
-
DFS(Depth First Search)를 사용하는 방법
첫 번째) BFS 방법
in_degree[N] 배열 : 정점에 들어오는 간선수를 저장. 정점 i로 들어오는 간선 수
- 모든 정점의 in_degree(진입차수)를 설정한다
- in_degree가 0인 정점은 visited 표시하고, 노드를 queue에 넣는다
- queue가 빌 때까지 아래를 반복한다
a. queue에서 원소를 꺼내T[]에 append한다
b. 꺼낸 정점에 인접한 정점 중 방문하지 않은 정점의 in_degree를 1 감소시킨다
c. in_degree 값이 0이면 해당 정점은 queue에 넣고 방문한 것으로 표시한다
두 번째) DFS 방법
BFS와 달리 in_degree를 사용하지 않고, 재귀를 사용한다.
- 모든 정점을 순회하며 방문하지 않은 정점에 대해서 DFS를 수행한다
- DFS 수행방식: 모든 정점을 탐색할 때까지 아래를 반복한다
a. 방문표시를 하면서 간선을 따라 다음 정점으로 방문한다
b. 더 이상 방문할 간선이 없으면 리스트 앞에 정점을 추가하고,
역추적(backtracking)을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인한다
c. 방문 가능한 간선이 있다면 다시 간선을 따라 다음 정점으로 이동한다
🏃 예시 문제 1
해답
처음에 선행 작업이 없는 노드가 1번 노드만 있는 게 아님을 유의하고 풀었어야 했다!
🤔풀이 사고 과정
1. 선행관계가 없을 때 작업을 동시에 수행할 수 있는 건 어떻게 처리할까?
만약, A일을 다 했는데 이로 인해서 두 개(혹은 그 이상)의 작업의 indegree가 0이 되었다
이럴 때는 어떻게 함? 그 뒤 작업이 B, C라고 하자. 그럼 B, C 둘 다 시작할 수 있다
- 두 개 이상의 작업을 동시에 시작할 수 있다고 한다
=> heap에 time을 같이 가지고 가야한다
- heap을 쓰는 이유 : 처음에는 선입선출 방식을 사용하기 위해 deque를 사용했는데, 작업이 동시에 진행될 수 있기 때문에 -> 해당 작업이 끝나는 시간이 가장 빠른 작업이 pop되게 하기 위하여 최소 heap을 사용하였다
import sys
import heapq
input = sys.stdin.readline
N = int(input())
takeTime = [0] * (N+1)
tasks = [[] for i in range(N+1)]
indegree = [0] * (N+1)
for i in range(1, N+1):
task = list(map(int, input().strip().split()))
takeTime[i] = task[0]
indegree[i] = task[1]
# 선행하는 일에 i를 넣기
for j in task[2:]:
tasks[j].append(i)
visited = [False] * (N+1)
heap = []
# 맨 처음에 indegree가 0인 작업들을 (시간, i) 먼저 넣어준다
for i in range(1, N+1):
if indegree[i] == 0:
heapq.heappush(heap, (takeTime[i], i))
result = 0
while heap:
time, task = heapq.heappop(heap)
visited[task] = True
# 내 뒤 선행 일의 indegree를 -1한다(완수했기 때문)
for t in tasks[task]:
indegree[t] -= 1
if indegree[t] == 0 and not visited[t]:
heapq.heappush(heap, (time + takeTime[t], t))
result = time
print(result)🏃 예시 문제 2
해답
🏃 예시 문제 3
해답
💯 Topological Sorting 문제를 더 풀어보고 싶다면?
골드
<BAEKJOON: 골드 5> 선수과목 (Prerequisite)
<BAEKJOON: 골드 4> 왕위 계승
<BAEKJOON: 골드 3> 게임 개발
<BAEKJOON: 골드 2> 문제집
<BAEKJOON: 골드 1> 최종 순위
플레티넘
<BAEKJOON: 플레티넘 5> 임계경로
<BAEKJOON: 플레티넘 5> 알고스팟어
<BAEKJOON: 플레티넘 4> 도미노
<BAEKJOON: 플레티넘 3> 여행 계획 세우기
<BAEKJOON: 플레티넘 2> ATM

