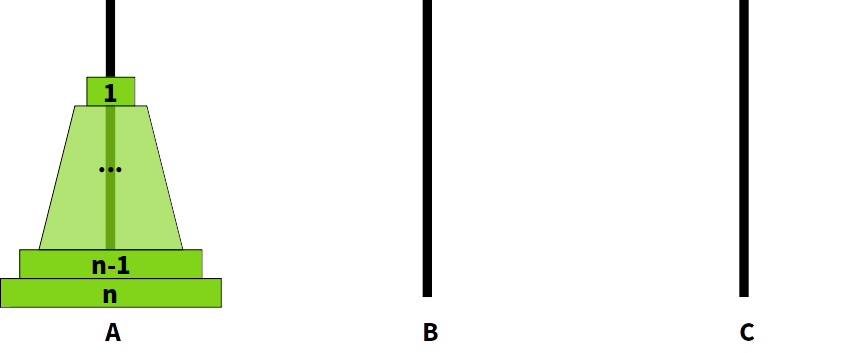
[문제]
https://www.acmicpc.net/problem/1155
레벨 : P5 (solved.ac)
알고리즘 분류 : DP
[접근]
(1) 옮겨야 할 디스크의 개수와 이동 우선 순위가 주어진다면 이동 순서와 횟수는 결정된다.
(2) 가장 큰 디스크는 비어있는 폴이 생기면 반드시 그쪽으로 이동하게 될 것이다.
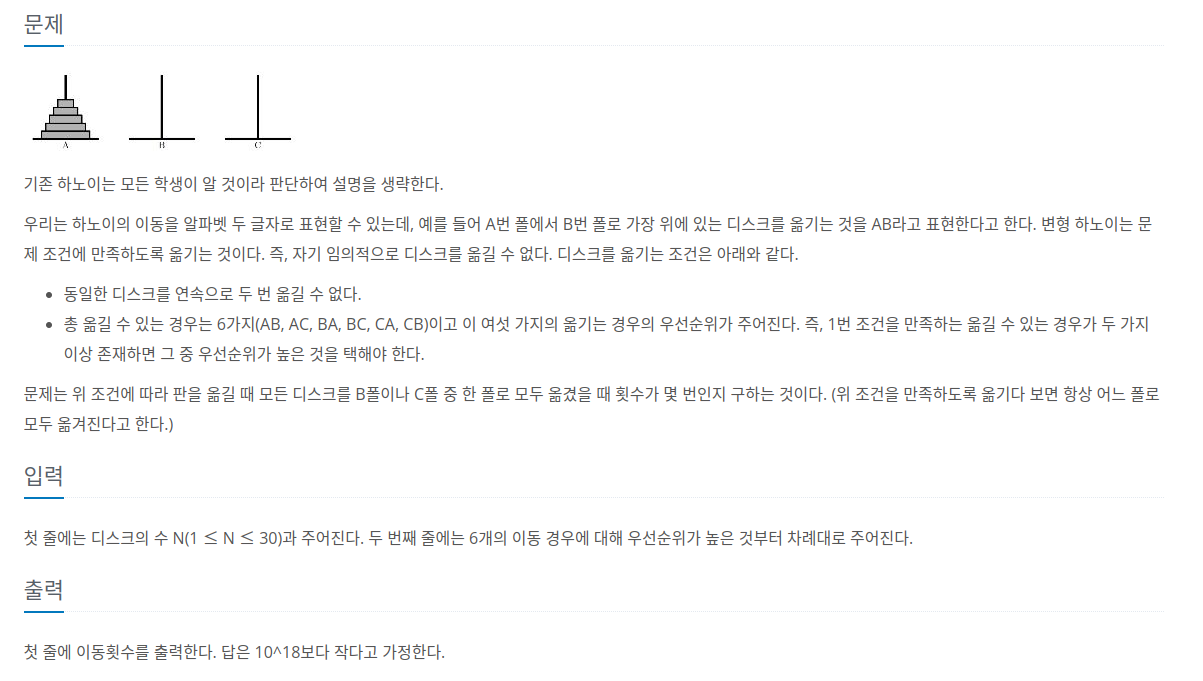
옮겨야 할 디스크의 개수가 n개일 때, 가장 작은 디스크부터 차례대로 1, 2, 3, ..., n번 디스크라고 하자.
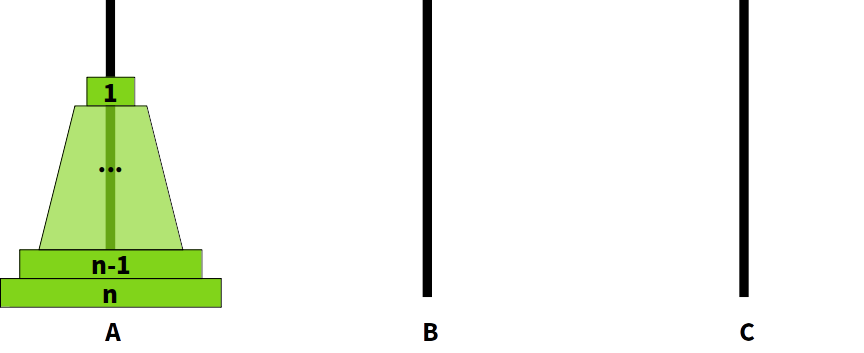
A폴에 있던 n개의 디스크들을 주어진 우선 순위에 따라 이동한 결과, 1~n-1번 디스크가 B폴로 옮겨졌다고 해보자.
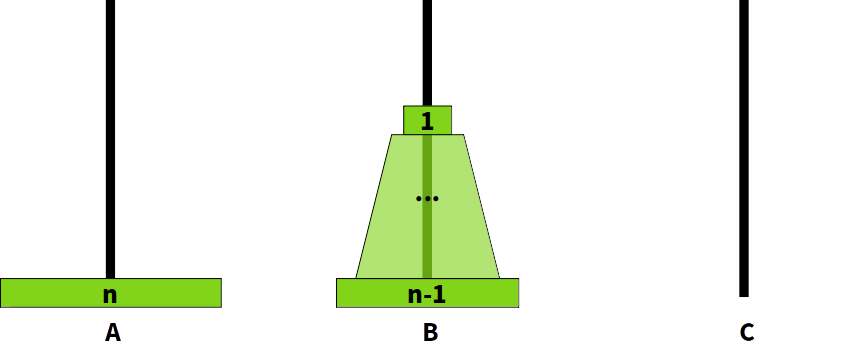
그렇다면 n번 디스크는 당연히 C폴로 이동하게 될 것.

이후에 가능한 경우에는 다음과 같이 두 가지가 있고, 이에 따라 이동하면 결국 n개의 디스크가 전부 B 또는 C폴에 쌓이게 된다!
case 1: n개의 디스크가 모두 B폴에 쌓이는 경우
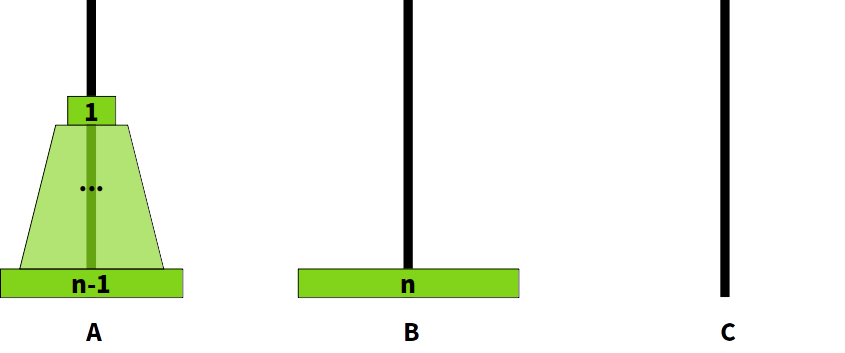
1) B에 있던 1~n-1번 디스크가 A폴로 이동
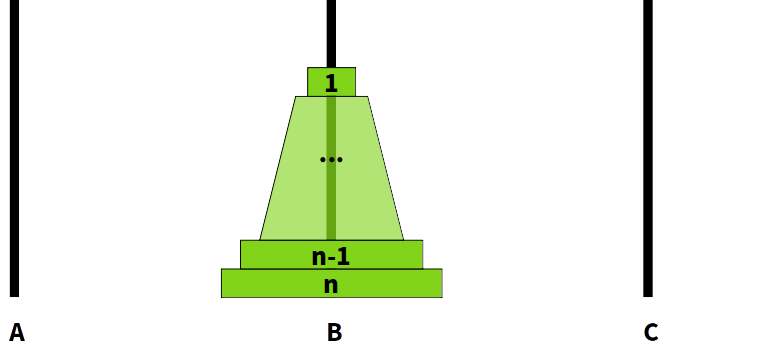
2) C폴에 있던 n번 디스크가 B폴로 이동
3) A폴에 있던 1~n-1번 디스크가 B폴로 이동 (clear)
case 2: n개의 디스크가 모두 C폴에 쌓이는 경우) B에 있던 1~n-1번 디스크가 C폴로 이동 (clear)
[코드]
#include <iostream>
using namespace std;
int main(){
int N; //전체 디스크의 개수
long long hanoi[3][3][31] = {0, };
char orders[6][3];
scanf("%d", &N);
for (int i = 0; i < 6; i++) {
scanf("%s", orders[i]);
orders[i][0] -= 'A';
orders[i][1] -= 'A';
}
for (int i = 0; i < 6; i++){
int from = orders[i][0], to = orders[i][1];
if (!hanoi[from][0][1] && !hanoi[from][1][1] && !hanoi[from][2][1]) hanoi[from][to][1] = 1;
}
for (int i = 2 ; i <= N; i++){
for (int from = 0; from < 3; from++){
for (int to = 0; to < 3; to++){
if (from != to){
if (hanoi[from][3-from-to][i-1] && hanoi[3-from-to][to][i-1]) hanoi[from][to][i] = hanoi[from][3-from-to][i-1] + 1 + hanoi[3-from-to][to][i-1];
else if (hanoi[from][to][i-1] && hanoi[to][from][i-1]) hanoi[from][to][i] = 2 * hanoi[from][to][i-1] + hanoi[to][from][i-1] + 2;
}
}
}
}
printf("%lld", hanoi[0][1][N] ? hanoi[0][1][N] : hanoi[0][2][N]);[코드 해설]
1) A, B, C 폴을 순서대로 0, 1, 2번 폴이라 하자.
hanoi[x][y][n]은 x번 폴에 n개의 디스크가 차례대로 쌓여있고 이것을 모두 y번 폴로 옮길 때 필요한 이동 횟수이다.
hanoi[x][y][n] == 0이라면,
- 이동이 필요하지 않거나(x ==y인 경우)
- 주어진 우선순위에 따라서는 이동이 불가능한 경우를 뜻한다.
hanoi배열은 처음에는 모두 0으로 초기화해놓도록 하자.
2) 주어진 우선 순위에 따라 n == 1인 경우를 채워주자.
hanoi[x][y][1]에 대해,
- x == y인 경우는 이동이 필요없으므로 패스.
- 나머지의 경우 우선순위에 따라 채워주면 된다.
예) 우선 순위가 AB AC BA BC CA CB 인 경우
AB가 AC에 우선하므로 hanoi[0][1][1] = 1, hanoi[0][2][1] = 0이다.
A, B, C폴에 디스크가 각각 1, 0, 0개 있을 때, 우선순위에 따라 디스크를 이동시키면 무조건 B폴로 가야하기 때문에.
3) 위 [접근] 에서 나온 것을 참고해 hanoi 배열을 차례로 돌면서 전부 채워준다. 두 케이스를 동시에 만족하는 경우는 없다.
(x번 폴도 y번 폴도 아닌 나머지 폴을 z번 폴이라고 하자)
x != y일 때, hanoi[x][y][n]은
- (case 1) hanoi[x][y][n-1], hanoi[y][x][n-1]이 모두 0이 아닌 경우
(== n-1개의 디스크를 x에서 y로, y에서 x로 옮기는 게 모두 가능한 경우)
- x폴에 있는 n-1개의 디스크를 y폴에 옮기고
hanoi[x][y][n-1]
- x폴에 있는 n번 디스크를 z폴에 옮긴다. (+1)
1 (hanoi[x][z][1]이 아니라)
- y폴에 있는 n-1개의 디스크를 다시 x로 옮긴 후
hanoi[y][x][n-1]
- z폴에 있는 n번 디스크를 y폴로 옮기고
1
- x폴에 있는 n-1개의 디스크를 다시 y폴로 옮긴다.
hanoi[x][y][n-1]
- (case 2) hanoi[x][z][n-1], hanoi[z][y][n-1]이 모두 0이 아닌 경우
(== n-1개의 디스크를 x에서 z로, z에서 y로 옮기는 게 모두 가능한 경우)
- x폴에 있는 n-1개의 디스크를 z폴로 옮기고
hanoi[x][z][n-1]
- x폴에 있는 n번 디스크를 y폴로 옮긴 후
1
- z폴에 있는 n-1개의 디스크롤 y폴로 옮긴다.
hanoi[z][y][n-1]
4) 전체 디스크의 개수 N개가 주어졌을 때, A폴에서 B폴 또는 C폴로 옮길 때 필요한 이동 횟수는?
- hanoi[0][1][N](A폴에 있는 N개를 B폴로 옮길 때의 이동 횟수)
또는
- hanoi[0][2][N](A폴에 있는 N개를 C폴로 옮길 때의 이동횟수)
중 0이 아닌 것(==가능한 경우)이다. (clear)
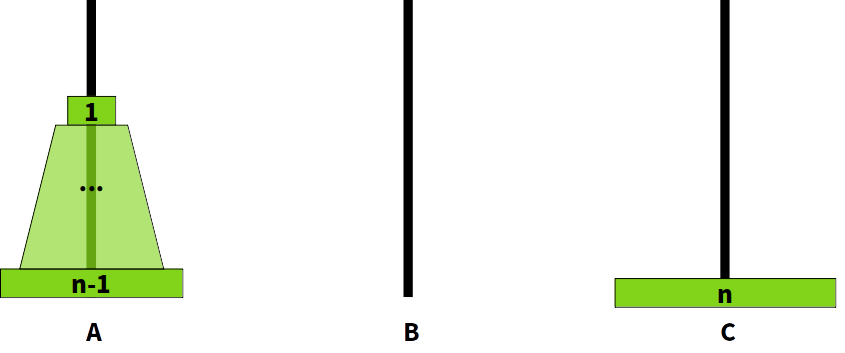
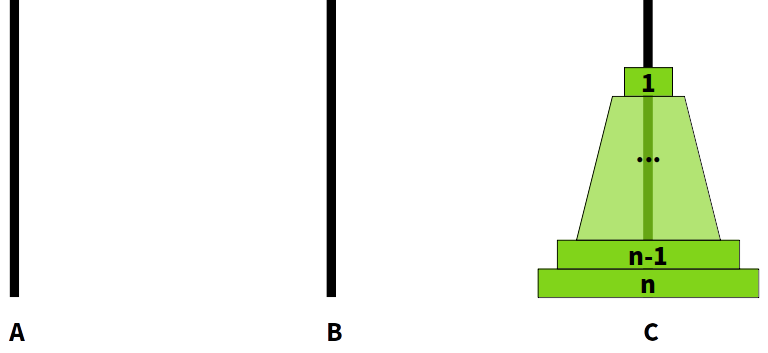

형 혹시 월클이세요?