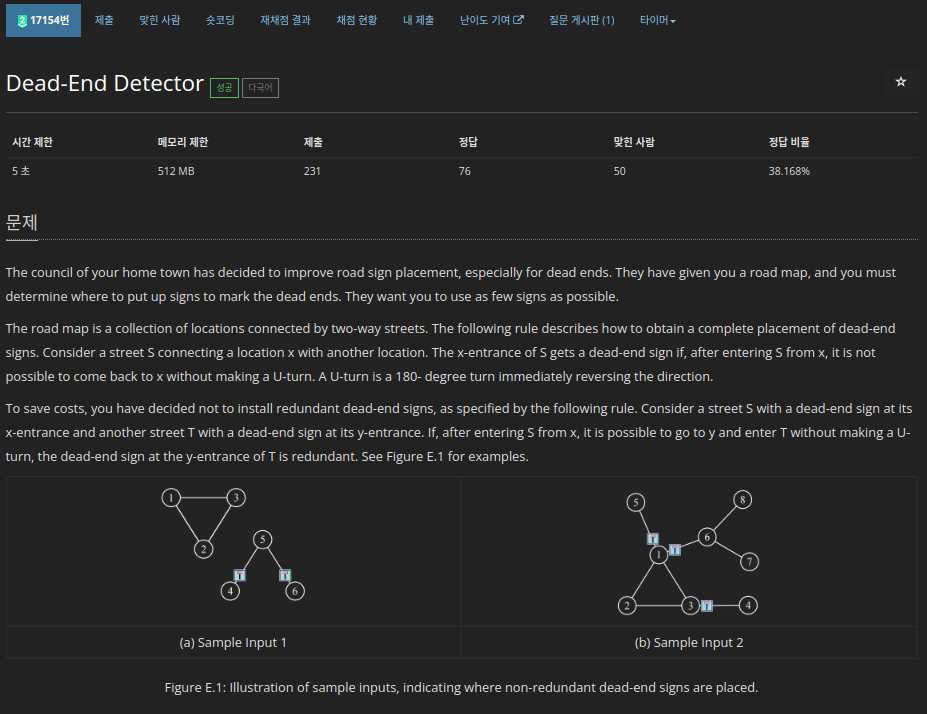
[1] 문제 요약
노드의 개수 과 (양방향)간선의 개수이 주어진다. 이후 개의 줄에는 간선으로 이어지는 두 노드의 번호가 주어진다.
그래프가 주어지면 막다른 길을 표시하기 위한 표지판을 어디에 세울지를 정해야 한다. 표지판을 세우는 기준은 다음과 같다.
- 그래프의 노드 x와 다른 노드를 연결하는 간선 S를 생각하자. x를 출발해, S를 지나서 유턴을 하지 않고서는 다시 x로 돌아올 수 없는 경우, S의 x-출입구 쪽에 표지판을 세운다. (유턴은 방향을 즉시 180도 바꾸는 것)
- 비용을 줄이기 위해 중복(redundant)되는 표지판은 설치하지 않는다. 예를 들어 x-출입구 쪽에 막다른 길 표지판이 설치된 간선 S, y-출입구 쪽에 표지판이 설치된 다른 간선 T를 생각해보자. x를 출발해 S를 지났을 때, y를 통해 유턴을 하지 않고 T를 통과할 수 있다면, T의 y-출입구 표지판은 중복이다.
[2] 표지판을 세우는 위치
문제의 샘플 인풋을 보고 그래프를 일단 다음과 같은 두 종류로 생각해보자. 아래서 는 노드 를 잇는 간선을, 는 해당 간선의 x-출입구를 가리킨다고 하자.
(1) 사이클
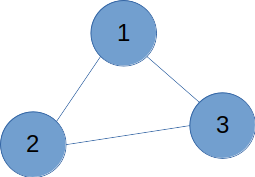
이런 사이클이 발생하는 그래프에는 표지판을 설치하지 않아도 된다. 1번 노드를 출발해 을 지나가보자. 를 지나면 유턴 없이 다시 1번 노드로 돌아올 수 있다. 간선 를 선택해 지나가도 마찬가지고, 다른 노드를 출발점으로 해도 마찬가지다.
(2) 트리
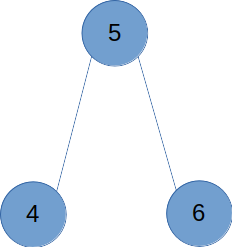
비순환 그래프의 경우에는 어떨까? 4번 노드에서 출발해보자. 를 통과해 다시 4번으로 돌아오려면 반드시 유턴이 있어야 하기 때문에, 번 노드를 잇는 간선의 4번-출입구에는 표지판이 세워져야 한다.
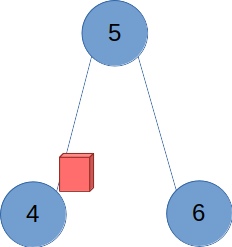
6번 노드를 출발해도 마찬가지다. 의 6번-출입구에 표지판이 세워진다.
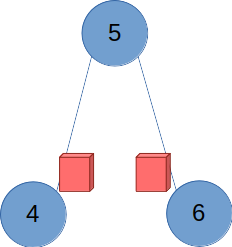
5번을 출발하는 경우는 어떨까? 를 통과했을 때 다시 자기 자신으로 돌아오려면 꼭 유턴을 해야하고, 를 통과해도 마찬가지다.
따라서 의 5번-출입구와 의 6번-출입구에도 표지판이 세워져야 한다.
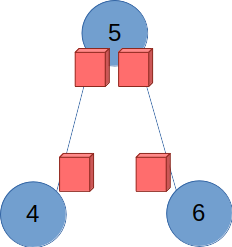
이제 중복 표지판을 없애보자. 4번을 출발해 를 지나갈 때, 5번에서 유턴 없이 을 지날 수 있으므로 표지판은 없어져도 된다. 5번, 6번도 마찬가지로 확인하면 마지막으로 남는 건 다음과 같다.

아래와 같은 트리를 생각해보자.
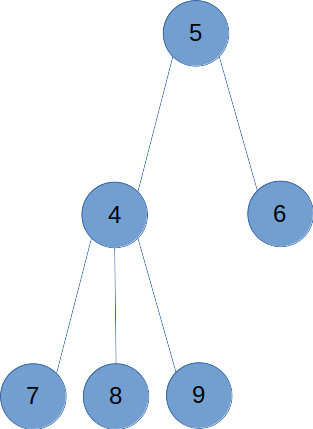
표지판을 세우고 중복을 제거하면 다음과 같은 결과가 된다.
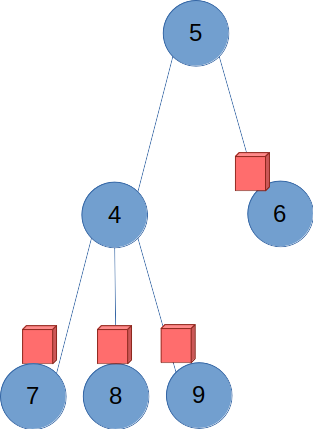
결국 트리에서 표지판은 리프 노드와 그 간선의 리프 노드-출입구 위에 세워진다.
단, 아래와 같이 두 개의 노드로만 이루어진 경우는 주의하자.
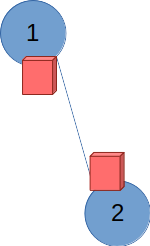
여기서 1, 2번 노드는 모두 리프 노드이기 때문에 간선의 양쪽 출입구 모두에 표지판이 세워진다.
(3) 조합
(1), (2)를 조합해서, 그래프의 종류를 좀 더 확장해보자.
사이클 + 사이클
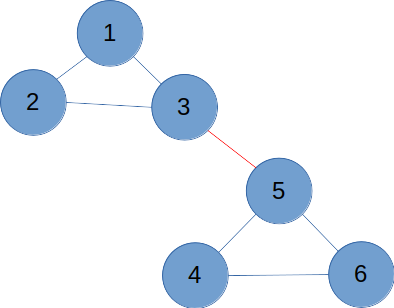
우선은 두 순환 그래프를 빨간색으로 표시된 간선으로 이었다고 해보자. 어느 노드, 어느 간선을 고르든 유턴을 하지 않고도 자기 자신으로 돌아올 수 있음을 확인할 수 있다.
사이클 + 트리
이번엔 사이클과 트리를 빨간 간선으로 연결해보자.
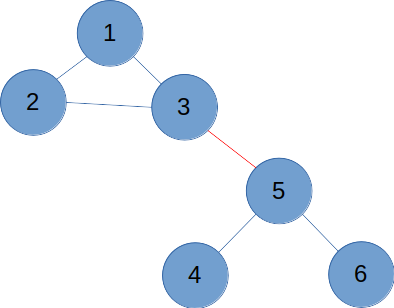
원래 사이클에 있던 노드와, 그것과 연결된, 원래 사이클에 있던 간선을 선택하는 경우, 자기 자신으로 유턴 없이 돌아올 수 있기 때문에 표지판을 세울 필요가 없다.
원래 트리에 있던 노드의 경우는 어떨까? 사이클과 연결된 노드(그림의 5번)를 출발해 사이클로 가는 간선()을 통과하는 경우, 유턴을 하지 않고도 자기 자신으로 돌아올 수 있다. (그림의 빨간 선)
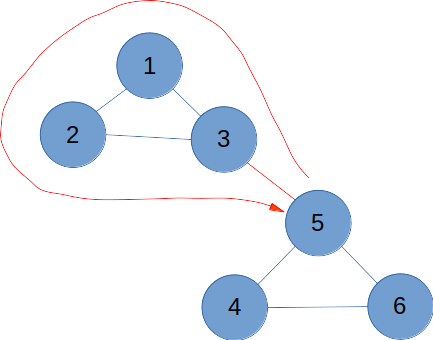
트리 내 다른 노드들은 어떨까? 양방향 간선 트리에서 임의의 두 노드를 선택하면 반드시 두 노드를 잇는 경로가 존재하므로, 트리 내에서 임의의 한 노드를 선택하면 사이클과 연결된 노드를 거쳐, 유턴을 하지 않고도 자기 자신에게 돌아올 수 있다.
예를 들어 6번 노드를 출발하면, 5번을 갈 수 있고, 사이클을 통해 다시 5번으로 돌아오고 6번으로 갈 수 있다.
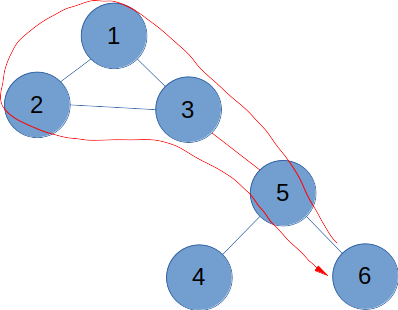
다만 사이클이 아니라 반대 방향으로 가는 경우에는 다르다. 트리의 리프 노드 방향으로 가는 경우, 유턴이 없이는 다시 자기 자신으로 돌아올 수 없다. 예를 들어 3번 노드를 출발해 를 지나는 경우를 확인해보자. 유턴이 없으면 자신으로 돌아올 수 없다. 5번을 출발해 을 지나는 경우도 마찬가지다. 따라서 다음의 위치에 모두 표지판이 세워지게 된다.
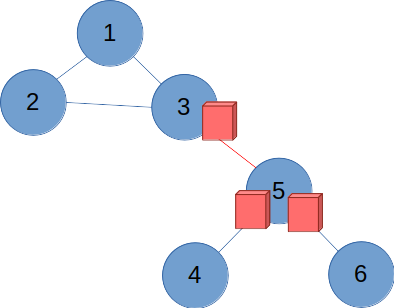
이제 중복되는 표지판을 지워보자 를 지나면 유턴을 하지 않고 5번을 지나 를 통과할 수 있으므로 표지판은 없어져야 한다. 마찬가지로 도 없어져야 한다.
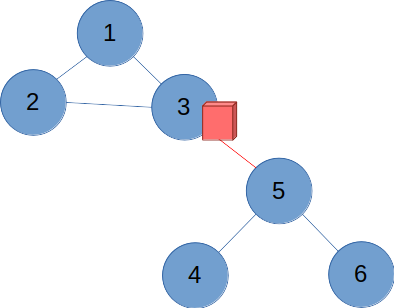
결과적으로, 사이클과 트리가 연결되는 경우, 둘을 연결하는 간선의 사이클 쪽 출입구에 표지판을 세우게 된다.
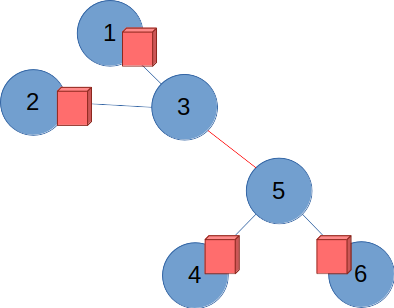
트리 + 트리
두 트리를 연결한 결과는 그 역시도 트리다. 앞에서와 마찬가지로 리프 노드와 연결된 간선의 리프 노드 쪽 출입구에 표지판을 세운다.
[3] 그래프 종류 알기
요약하자면 다음 위치에 표지판을 세우게 된다.
- 사이클이거나 사이클끼리 연결된 경우, 표지판을 세우지 않는다.
- 트리인 경우, 리프 노드와 연결된 간선의 리프 노드 방향 출입구에 표지판을 세운다.
- 사이클에 트리가 붙은 경우, 사이클 쪽 노드를 C, 트리 쪽 노드를 T라 할 때, 에 표지판을 세운다.
그래프가 어떤 종류인지 알게 되면 표지판을 어디에다가 세워야 할지를 알 수 있게 된다. 그럼 그래프가 사이클(혹은 사이클끼리 연결된 그래프)인지, 트리인지, 혹은 사이클에 트리가 붙은 경우인지는 어떻게 알 수 있을까?
(1) 그래프에 사이클이 있는 경우
사실 1. 사이클이거나 사이클끼리 연결된 경우와 3. 사이클에 트리가 붙은 경우는 똑같이 생각해줘도 좋다. 다음과 같은 그래프를 생각해보자.
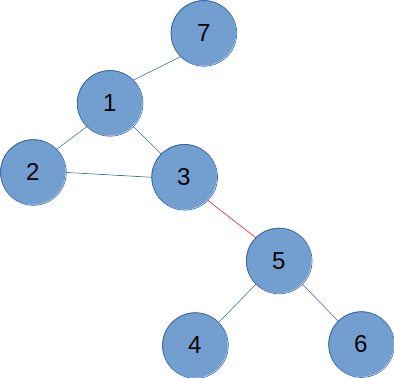
각 노드들에 스스로와 연결된 노드의 간선의 개수, 즉 차수(degree)를 적어 주면 다음과 같다.
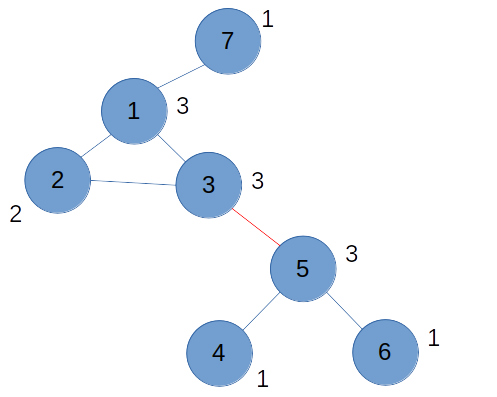
차수가 1인 노드들은 리프 노드다. 리프 노드들을 시작점으로 BFS를 진행한다.
BFS에서는 큐에 담긴 노드를 삭제하고, 연결된 노드에서도 차수를 1씩 줄여준다. 예를 들어 위 그래프의 리프 노들이 모두 삭제되면 다음과 같이 된다. 리프 노드들이 삭제되고, 이 노드들과 연결된 1, 5번 노드들의 차수가 줄어들었다.
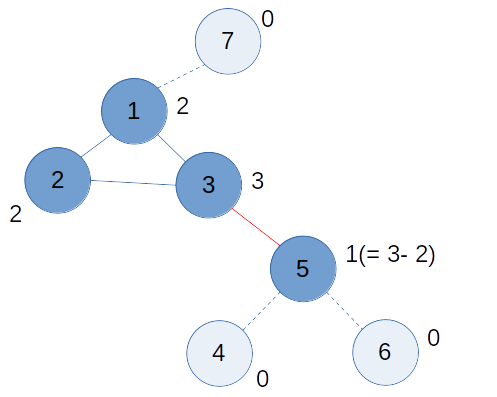
4, 6번이 사라지면서 5번이 리프 노드가 됐으니, 5번도 큐에 넣고 BFS를 이어간다. 5번이 삭제되면 그래프는 다음과 같이 된다.
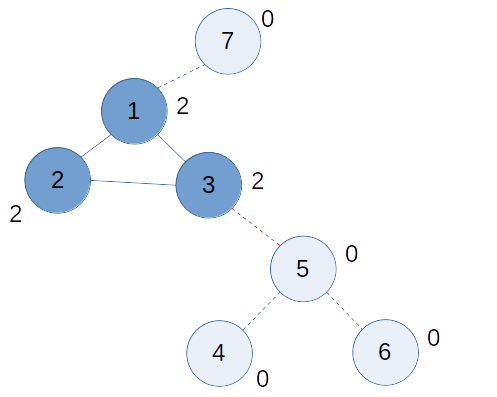
이제 더 이상 남아있는 리프 노드가 없다. 이제 각 노드의 차수를 봤을 때, 0보다 큰 것 노드들이 남아 있으면, 해당 노드들은 사이클에 속하는 노드들이다.
사이클에 트리가 붙은 경우, 사이클 쪽 노드를 C, 트리 쪽 노드를 T라 할 때, 에 표지판을 세운다.
여기서 노드 는 차수가 0보다 큰 노드들 중 하나고, 는 차수가 0인 노드 중 하나다. 따라서 각 노드들의 남은 차수를 확인하고, 차수가 0보다 큰 노드()가 나타나면 해당 노드와 연결된 노드들을 확인해보자. 연결된 노드에 차수가 0인 노드()가 있다면 에는 표지판이 세워진다.
(2) 트리인 경우
위와 마찬가지로 BFS를 진행했을 때, 차수가 0보다 큰 노드가 남아있지 않으면 그 그래프는 트리가 된다.
(3) 근데?
그런데 문제는 주어진 그래프가 하나의 컴포넌트만이 아니라, 다음과 같이 복수의 컴포넌트로 이루어졌을 수도 있다는 점이다.
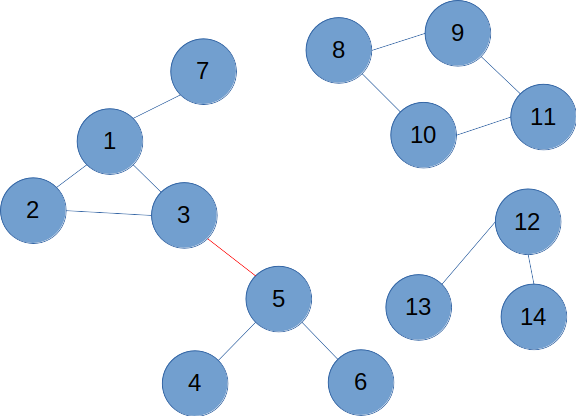
따라서 큐에 들어간 노드가 어떤 컴포넌트에 속한 것인지도 알 수 있어야 한다. BFS를 하면서 각 리프노드가 어떤 노드와 연결됐는지를 저장하자. BFS 중에 union-find로 큐에 들어간 노드의 그룹을 함께 기록해주자.
위 그래프에 이 방법을 적용시키고, 각 노드들의 BFS 이후의 차수를 확인하자.
- 만약 차수가 0보다 크면 해당 노드는 사이클을 이루는 컴포넌트에 들어있다. 해당 노드와 연결된 노드들의 차수를 확인해보자.
- 만약 차수가 0이라면 해당 노드의 그룹을 확인한다.
- 만약 이 노드와 연결된 간선의 개수가 1개라면, 이 노드는 원래 리프 노드다.
- 그렇지 않다면, 이 노드는 BFS 중에 사라지게 된 노드다.
- 이 노드가 원래 리프 노드일 때, 노드가 속한 그룹의 루트의 차수가 0이라면, 이 노드가 속한 컴포넌트는 트리다. 그렇지 않으면 이 노드가 속한 컴포넌트에는 사이클이 존재한다.
[4] 코드
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
const int MAX_N = 5 * 10e5;
int N, M;
int degree[MAX_N + 1];//degree가 0 이하면 삭제된 노드다.
int parent[MAX_N +1];//노드가 속한 그룹
vector<vector<int>> adj;
vector<pair<int, int>> dead_signs;
queue<int> q; //BFS를 위해 리프노드들을 넣는 큐
int find(int a) {
if (parent[a] == a) return a;
return parent[a] = find(parent[a]);
}
void uni(int a, int b) {
a = find(a), b = find(b);
if (a == b) return;
parent[a] = b;
}
int main(){
scanf("%d%d", &N, &M);
adj.resize(N + 1);
for (int i = 1; i <= N; i++) parent[i] = i;
for (int i = 0; i < M; i++){
int v, w;
scanf("%d%d", &v, &w);
adj[v].push_back(w);
adj[w].push_back(v);
degree[v]++;
degree[w]++;
}
// degree가 1이면 리프노드다.
for (int i = 1; i <= N; i++) {
if (degree[i] == 1) {
q.push(i);
}
}
// BFS를 진행
while (!q.empty()) {
int front = q.front();
q.pop();
degree[front]--;
for (int next : adj[front]) {
if (degree[next] <= 0) continue;//삭제된 노드인 경우는 확인하지 않음
uni(front, next);
degree[next]--;
if (degree[next] == 1) {//리프라서 곧 지워질 것. 큐에 넣음
q.push(next);
}
}
}
// 각 노드들의 BFS 이후 결과 차수를 확인한다.
for (int i = 1; i <= N; i++) {
if (degree[i] > 0) {//사이클에 포함된 노드인 경우.
for (int next: adj[i]) {
if (degree[next] <= 0) {
dead_signs.emplace_back(i, next);
}
}
}
else if (adj[i].size() == 1 && degree[find(i)] <= 0){//원래 리프노드 였고, 해당 노드가 속한 컴포넌트의 루트 노드가 삭제된 경우
dead_signs.emplace_back(i, adj[i][0]);
}
}
// 명시된 출력 방식에 따라 정렬한다.
sort(dead_signs.begin(), dead_signs.end());
printf("%lu\n", dead_signs.size());
for (auto dead_sign : dead_signs) {
printf("%d %d\n", dead_sign.first, dead_sign.second);
}
}
`
아유 어려워 다음에 읽으러 오겠습니다