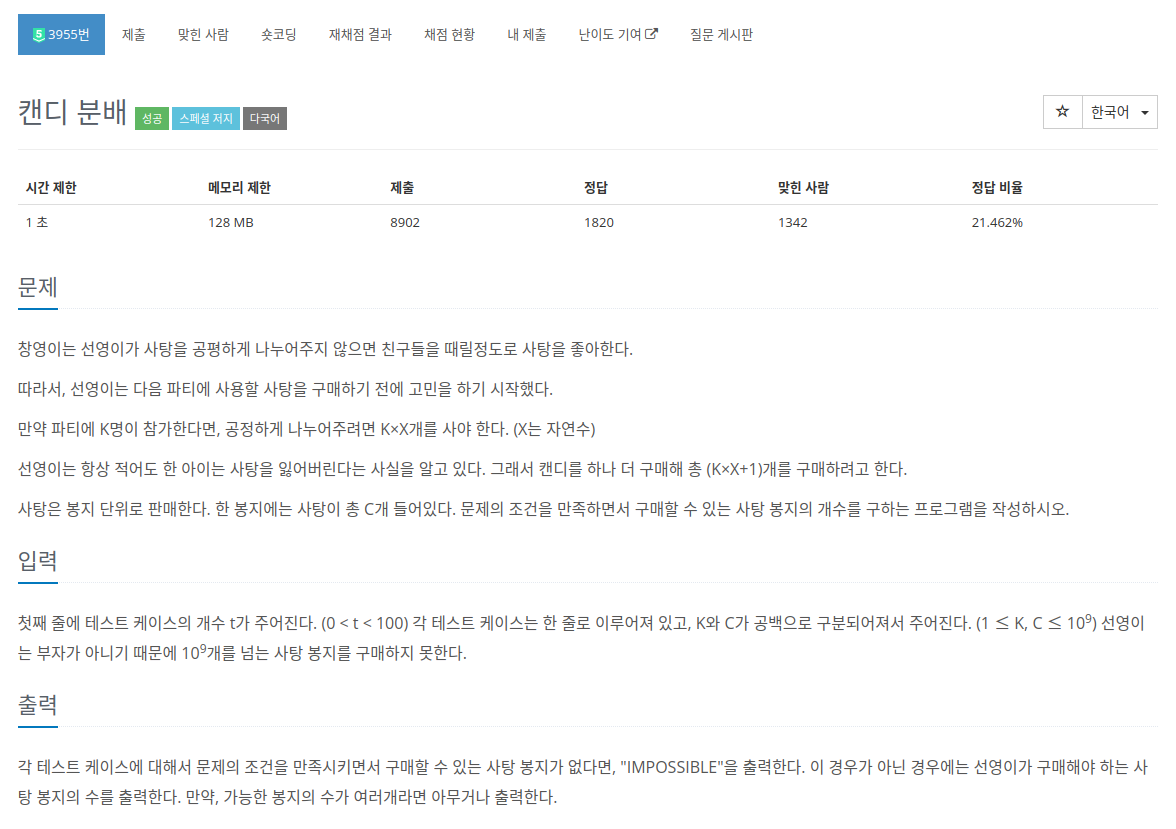
https://www.acmicpc.net/problem/9202
레벨 : P5
알고리즘 분류 : 수학, 정수론, 확장 유클리드 호제법
[1] 문제 요약
각 테스트 케이스에 대해 와 가 주어졌을 때, 가 되는 자연수 를 구하는 문제다. (단 Y <= 1,000,000,000)
[2] Preliminary
✏️ 참고할 만한 정수론 정수론 자료 (링크는 서울대학교 권오남 교수님의 SNUON 정수론 강의 내용 정리)
필요한 것들만 뽑아서 정리하자면 다음과 같다.
정수 에 대해서 다음이 성립한다.
(1)인 정수 가 존재 가 서로소.
(2)이면
(3)이면 인 정수 에 대해서도
위 (3)은 의 특수해 을 구하면 의 일반해 도 구할 수 있다는 것을 의미한다.
[3] 유클리드 호제법
0이 아닌 두 정수 의 최대 공약수를 구하는 유클리드 호제법은 아래와 같다.
이는 코드로 다음과 같이 나타낼 수 있다.
int gcd(int a, int b){
int dividend = a;
int divisor = b;
int quotient;
int remainder;
while (a && b){
quotient = dividend / divisor;
remainder = dividend % divisor;
printf("%d = %d * %d + %d\n", dividend, quotient, divisor, remainder);
if (remainder == 0) return divisor;
dividend = divisor;
divisor = remainder;
}
return -1; //입력 a, b 중 하나라도 0인 경우 -1을 리턴해서 연산이 제대로 되지 않았음을 표시했습니다.
}
[4] 확장 유클리드 호제법
앞서 이면 라는 정리를 적어놨는데, 확장 유클리드 호제법은 일 때, 즉 가 될 때의 정수해 를 구하는 알고리즘이다.
유클리드 호제법에서 나타나는 나머지 (임에 주의)이 모두 의 일차결합으로 표현될 수 있고, 위에서도 볼 수 있듯 각 나머지들 사이에서는 의 관계가 성립한다.
를 일반화해 다음과 같이 쓰도록 하자.
그러면 앞서의 나머지들 사이의 관계 를 이용해 다음과 같은 의 점화식을 얻을 수 있다.
여기서 라고 놓으면 의 초항들 을 얻을 수 있다.
위를 그대로 코드로 쓰면 아래와 같다.
/*
ax + by = (a,b)가 되는
{{x, y}, (a,b)}를 찾는 함수
*/
pair<pair<int,int>, int> extendedGCD(int a, int b){
int dividend = a, divisor = b;
int quotient, remainder;
int s_prev = 1, s_cur = 0, s_next;
int t_prev = 0, t_cur = 1, t_next;
while (a && b){
quotient = dividend / divisor;
remainder = dividend % divisor;
if (remainder == 0) return {{s_cur, t_cur}, divisor};
s_next = s_prev - quotient * s_cur;
t_next = t_prev - quotient * t_cur;
s_prev = s_cur, s_cur = s_next;
t_prev = t_cur, t_cur = t_next;
dividend = divisor;
divisor = remainder;
}
return {{-1, -1}, -1}; //잘못된 입력의 경우
}[5] 문제 풀이
앞서 문제 요약에서 말했듯 이 문제는 자연수 와 가 주어졌을 때, 가 되는 자연수 를 구하는 문제, 즉 의 자연수 해 를 구하는 문제다.(단 Y <= 1,000,000,000)
우리는 [2]Preliminary를 통해 인 정수 가 존재한다는 것은 가 서로소라는 것과 동치이고, 의 특수해를 안다면 그로부터 그 일반해도 얻을 수 있음을 알고 있다.
확장 유클리드 호제법을 통해서 우리는 의 최대공약수와 의 특수해 를 구할 수 있고, 문제에서는 의 자연수 해를 구하는 것이 목적이니 특수해 를 통해 가 되는 정수를 구하면 된다.
[6] CODE
#include <iostream>
using namespace std;
int n, k, c, T;
pair<pair<int, int>, int> extendedGCD(int a, int b){
int dividend = a, divisor = b;
int q, r;
int s_prev = 1, s_cur = 0, s_next;
int t_prev = 0, t_cur = 1, t_next;
while (a && b){
q = dividend / divisor;
r = dividend % divisor;
if (!r) return {{s_cur, t_cur}, divisor};
s_next = s_prev - q * s_cur;
t_next = t_prev - q * t_cur;
s_prev = s_cur, s_cur = s_next;
t_prev = t_cur, t_cur = t_next;
dividend = divisor;
divisor = r;
}
return {{-1, -1}, -1};
}
int main(){
scanf("%d", &T);
while (T--){
scanf("%d%d", &k, &c);
pair<pair<int, int>, int> extdGCD = extendedGCD(k, c); //확장 유클리드 호제법을 사용
/*
만약 K, C가 서로소가 아니라면
-KX + CY = 1의 정수해 X, Y는 존재하지 않는다.
*/
if (extdGCD.second != 1) printf("IMPOSSIBLE\n");
else {
int x = extdGCD.first.first; //-KX+CY=1의 특수해 x
int y = extdGCD.first.second; //특수해 y
while (!(x < 0 && y > 0)){ //x <0, y> 0이 되어야 한다.
x -= c; //[2]Preliminary의 (3)을 참고
y += k;
}
//문제의 제약에 따라 y는 1,000,000,000 이하가 되어야 하므로 확인해본다.
while ((x < 0 && y > 0) && !(y <= 1000000000)){
x += c;
y -= k;
}
//x < 0, 0 < y <= 1,000,000,000이 되는 해가 존재하지 않는 경우 "IMPOSSIBLE"
if (!(x < 0 && y > 0 && y <= 1000000000)) printf("IMPOSSIBLE\n");
else printf("%d\n", y);
}
}
}