1. 에드먼즈-카프 리뷰

에드먼즈-카프 알고리즘은 다음과 같이 진행했다.

1. BFS를 통해 잔여 네트워크 $G_f$에서의 s->t 최단 경로를 찾아, 이를 증가 경로로 설정한다.
2. 증가 경로 상의 간선 중 최소 잔여 용량을 가지는 것을 골라, 그 용량만큼을 흘려 보낸다.
3. 더 이상 증가 경로를 찾을 수 없을 때까지 1-2를 반복

$s \rightarrow t$ 최단 경로를 하나 찾아 흐름을 보내는 데에 $O(|E|)$의 시간이 걸리고, 최단 경로의 개수는 $O(|V||E|)$개 이므로 전체 시간복잡도는 $O(|V||E|^2)$이다.

그런데 굳이 증가 경로를 하나씩 찾지 않고, 한 번에 여러 개를 찾아 흐름을 보낼 수 있다면 조금 더 빠르게 최대 유량을 찾아낼 수도 있지 않을까? 우리는 다음의 사실을 알고 있다.

에드먼즈-카프 알고리즘을 수행하는 경우(즉 $s \rightarrow t$ 최단 경로를 증가 경로 $p$로 두고, $f_p$를 추가로 흘려보내는 경우), 잔여 네트워크 $G_f$에서의 $s, t$ 최단 거리 $\delta_f(s,t)$는 단조 증가한다.

경로 $s \rightarrow t$의 길이는 길어봐야 $|V| - 1$이기 때문에, 경로의 길이가 같은 것들을 묶어 한 번에 처리할 수 있다면 $O(|V|)$번만 반복해도 최대 유량 문제를 해결할 수 있다.

디닉 알고리즘이 바로 $\delta_f(s, t)$가 같은 것들을 묶어 한 번에 처리하는 알고리즘으로, $O(|V|^2|E|)$의 시간복잡도를 가진다. $|E|$는 적어도 O($|V|$)에 많으면 $O(|V|^2)$이니, 에드먼즈-카프 알고리즘보다는 좀 더 빠르다.

2. 디닉 알고리즘(Dinic's Algorithm)

우리에게는 "디닉 알고리즘"으로 잘 알려져 있지만, 사실은 이 알고리즘을 고안한 디니츠(Dinitz)의 이름이 잘못 알려져서라고 한다.

(1) Layered Network(Level Graph)

임의의 유향 그래프 $H=(V, E)$와 시작 정점 $s$를 생각해보자. $s$에서 시작해 BFS를 진행하면 $s$와 다른 모든 정점 사이의 최단 거리를 구할 수 있고, 이를 기준으로 $V$와 $E$를 몇 개의 부분 집합으로 나눌 수 있다. $\delta(u, v)$는 $u$에서 $v$로의 최단 거리다.

정점 레이어(vertex layer)
$i$번째 정점 레이어 $V_i$는 $s$로부터의 최단 거리가 $i$인 모든 정점들의 집합이다.

$V_i = \{v : v \in V, \delta(s, v) =i\}$

간선 레이어(edge layer)
$i$번째 간선 레이어 $E_i$는 $V_{i-1}$에서 $V_i$로 이어지는 모든 간선들의 집합이다.

$E_i = \{(u, v): (u, v) \in E, u \in V_{i - 1}, v \in V_i\}$

이렇게 $V, E$의 부분 집합들을 가지고 새롭게 유향 그래프 $L(s)$를 정의해보자.

레이어드 네트워크(layered network)
유향 그래프 $H = (V, E)$와 시작 정점 $s$가 주어졌을 때, 레벨 그래프 $L(s)$는 $s$로부터 도달할 수 있는 $H$의 모든 정점들과 해당 정점들로의 최단 경로 상에 있는 모든 간선들로 이루어진 유향 그래프다.

$L(s) = (\cup V_i, \cup U_i)$

어떤 정점 $t \in V$가 있다고 해보자. $L(s)$를 이용하면 모든 $s \rightarrow t$ 최단 경로들도 찾을 수 있다. $s$에서 시작해 $t$로 끝나는 최단 경로들에 포함된 모든 정점들과 간선들로 이루어진 그래프를 $\hat{L}(s, t)$라 하자. $\hat{L}(s, t)$는 $L(s)$를 구성한 후, $t$에서 역방향으로 BFS를 수행하면 얻을 수 있다.

(2) 정리와 증명들

$s$를 소스, $t$를 싱크로 갖는 유량 네트워크 $G = (V, E)$와 흐름 $f$가 주어졌을 때, 잔여 네트워크 $G_f$를 가지고 레이어드 네트워크 $\hat{L_f}(s, t) =(\hat{V_f}, \hat{E_f})$를 만들었다고 해보자(이후 $(s,t)$ 생략).

에드먼즈-카프 알고리즘에서 그랬듯 $G_f$의 $s \rightarrow t$ 최단 경로를 하나 골라 증가 경로 $p$로 선택하자. 이 경로는 당연히 $\hat{L_f}$에서 찾을 수 있다. 이 경로를 따라 $f_p$의 유량을 추가로 흘렸을 때 유량의 값은 $|f'|$가 된다고 해보자.

이제 $G_{f'}$에서 다음 증가 경로 $p'$를 찾아야 한다. 증가 경로의 길이는 단조 증가하므로 $p'$의 길이는 $p$보다 길거나 같은데, 두 경로의 길이가 서로 같은 경우를 생각해보자.

만약 에드먼즈-카프 알고리즘을 사용했다면 또 $O(|E|)$의 시간을 들여 증가 경로를 찾아야 했겠지만, 다행히 우리는 이미 찾아놓았던 $\hat{L_f}$를 활용할 수 있다.

Theorem 1

$G_f$의 레이어드 네트워크 $\hat{L_f}$에서 $p$의 핵심 간선들을 제거한 것을 $\hat{L'_f} = (\hat{V'_f},\hat{E'_f})$라 하자. $G_f$에 $|f_p|$의 흐름을 추가로 보낸 후의 잔여 네트워크를 $G_{f'} = (V_{f'}, E_{f'})$라 할 때 다음이 성립한다.

$\hat{E'_f} \subseteq E_{f'}$

위 정리를 이용하면 $\hat{E'_f}$에서 찾은 $s \rightarrow t$ 경로를 $G_{f'}$의 증가 경로로도 사용할 수 있다.

$pf.$
$G_f$에 $\hat{L_f}$에서 찾은 $s \rightarrow t$ 최단 경로 $p$를 따라 $f_p$의 유량을 추가로 흘려보냈을 때 어떤 일이 일어나는지를 생각해보자. $(u, v)$가 $p$ 위의 간선일 때,

1. $(u, v)$가 $p$의 핵심 간선이라면, 잔여 용량이 $c_f(u, v) = 0$이 되어 잔여 네트워크에서 사라진다.
2. $G_f$에서 $f(u, v) = 0$이었다면, 유량 증가 이후 간선 $(v, u)$가 $c_{f'}(v, u) = f_p$의 용량을 가지고 잔여 네트워크에 추가된다.

$E_{f'}$가 $E_f$와 달라지는 경우는 위의 두 경우 밖에 없다. 즉 $E_{f}$에서 $p$의 핵심 간선들을 삭제하고, $p$ 위의 간선 몇 개의 역방향 간선이 추가하면 $E_{f'}$를 만들 수 있다. 한편 $\hat{E'_f}$는 $E_f$의 부분집합이며, $p$의 핵심 간선들을 삭제하기만 한 것이기 때문에 $E_{f'}$의 부분집합이 된다.

Lemma

$G$에서 에드먼즈-카프 알고리즘을 실행할 때, 모든 정점 $v \in V$에 대해 매 유량 증가마다 잔여 네트워크 $G_f$에서의 $\delta_f(s, v)$와 $\delta_f(v, t)$는 단조 증가한다.

$pf.$
이전 글에서 매 유량 증가마다 $\delta_f(s,v)$가 단조 증가함은 보인 적이 있다. 마찬가지의 방법으로 매 유량 증가마다 $\delta_f(v, t)$ 또한 단조 증가함을 보일 수 있다.

Theorem 2

$G_{f'}$의 레이어드 네트워크를 $\hat{L_{f'}} = (\hat{V_{f'}}, \hat{E_{f'}})$라 할 때, $\delta_{f'}(s, t) = \delta_f(s, t)$라면 $\hat{E_{f'}} \subseteq \hat{E'_f}$다.

이제 $G_{f'}$를 가지고 레이어드 네트워크 $\hat{L_{f'}}$를 만든다고 해보자. $G_{f'}$의 모든 $s \rightarrow t$ 최단 경로는 $\hat{L_{f'}}$를 통해 찾을 수 있다. 만약 $\delta_{f'}(s, t) = \delta_f(s, t)$이면서 $\hat{L_{f'}}$에서 찾을 수 있는 모든 임의의 $s \rightarrow t$ 최단 경로를 $\hat{L'_f}$에서도 찾을 수 있다면, $\hat{L'_f}$만으로도 $G_{f'}$의 증가 경로를 찾을 수 있게 될 것이다.

$pf.$
$\hat{L_{f'}}$에서는 찾을 수 있지만, $\hat{L'_f}$에서는 찾을 수 없는 $s \rightarrow t$ 최단 경로가 있다고 가정하자. 만약 그렇다면 이 경로에는 $\hat{E_{f'}}$에서는 찾을 수 있지만 $\hat{E'_f}$에서는 찾을 수 없는 간선이 하나 이상 포함되어 있다. 그 중 하나를 $(u, v)$라 한다면 다음의 두 경우가 가능하다.

1. $(u, v) \in E_f$인 경우

만약 $(u, v) \in \hat{E_f}$였다면 이 간선은 $G_f$에서 찾았던 증가 경로 $p$를 따라 흐름을 보내면서 삭제된 간선이어야 한다. 하지만 이렇게 삭제된 간선은 $G_{f'}$에서도 여전히 삭제된 상태이므로 $\hat{E'_f}$에 포함될 수 없다.

그렇다면 $(u, v) \not\in \hat{E_f}$라 해보자. 이는 $G_f$에서 찾을 수 있는 $s \rightarrow t$ 최단 경로들에 $(u, v)$ 간선이 포함되지 않는다는 것이다. $(u, v)$를 포함하는 $s \rightarrow t$ 경로 중 가장 짧은 것은 $s \rightarrow u$ 최단 경로, $(u, v)$, $v \rightarrow t$ 최단 경로를 거치는 것이고, 그 길이는 $\delta_f(s, u) + \delta_f(v, t) + 1$이다.

한편 $(u, v) \in \hat{E'_f}$이므로 이 간선은 $G_{f'}$에서의 $s \rightarrow t$ 최단 경로들 중 적어도 하나에는 포함되고, 그 길이는 $\delta_{f'}(s, u) + \delta_{f'}(v, t) + 1$이다.

그런데 위 Lemma에 따르면 $\delta_f(s, u) \leq \delta_{f'}(s, u)$이고 $\delta_f(v, t) \leq \delta_{f'}(v, t)$여야 한다. 이는 $\delta_f(s,t) = \delta_{f'}(s,t)$라는 가정과 모순이다.

따라서 $(u, v)$는 $E_f$의 원소일 수 없다.

2. $(u, v) \not\in E_f$인 경우

$(u, v)$는 $\hat{E_{f'}}$의 원소이므로 $(u, v) \in E_{f'}$다. $(u, v) \not\in E_f$였다가 유량 증가와 함께 $(u, v) \in E_{f'}$가 됐을 때, 가능한 경우는 $f(v, u) = 0$인 간선 $(v, u)$가 경로 $p$ 위에 존재하다, 유량이 증가하면서 $c_f(u, v) = f_p$인 간선 $(u, v)$가 잔여 네트워크에 추가되는 경우 밖에 없다.

$(v,u)$가 $p$에 포함되는 간선이므로 다음과 같이 쓸 수 있다.

또한 $(u, v) \in \hat{E_{f'}}$로부터 다음과 같이 쓸 수 있다.

이 둘을 더하면 아래와 같다($\delta_f(s,t) = \delta_{f'}(s, t)$를 가정했으므로).

위 Lemma에 따라 $\delta_f(s, v) + \delta_f(v, t) = \delta_f(s, t) \leq \delta_f(s, v) + \delta_{f'}(v, t)$이고, $\delta_f(s, u) + \delta_f(u, t) = \delta_f(s, t) \leq \delta_{f'}(s,u) + \delta_f(u, t)$이므로, 다음과 같은 모순이 발생한다.

따라서 $(u, v) \not\in E_f$도 있을 수 없다.

어떠한 경우에도 모순이므로 $(u, v) \in \hat{E_{f'}}$이면서 $(u, v) \not\in \hat{E'_f}$인 간선은 존재할 수 없다. 따라서 $\hat{E_{f'}} \subseteq \hat{E'_f}$다.

(3) 중간 정리와 데드엔드

지금까지 알아낸 사실들을 정리해보자.

중간 정리
1. 잔여 네트워크 $G_f$가 주어진다면 레이어드 네트워크 $\hat{L_f}$를 만든다. $\hat{L_f}$에서 $s \rightarrow t$ 최단 경로 $p$를 찾을 수 있다면 이는 $G_f$의 증가 경로다.
2. $p$를 따라 $f_p$의 흐름을 보냈을 때, 유량이 $f'$로 증가했다고 하자. 잔여 네트워크 $G_{f'}$에 존재하는 최단 증가 경로 $p'$의 길이가 $p$와 같다면, 그 $p'$ 도 $\hat{L_f}$(정확히는 $\hat{L_f}$에서 $p$의 핵심 간선들이 제거된 $\hat{L'_f}$)에서 찾아낼 수 있다(Theorem 1과 2).

어떠한 흐름도 없는 초기 상태에서부터 더 이상 유량을 증가시킬 수 없을 때까지 잔여 그래프의 $s \rightarrow t$ 최단 경로를 따라 유량을 증가시키기를 반복할 때, 그 증가 경로의 길이는 단조 증가한다.

이때 증가 경로의 길이가 같은 것들을 묶은 것을 페이즈(phase)라고 해보자. 증가 경로의 길이가 $\ell$인 페이즈의 맨 첫 번째 잔여 그래프를 $G_\ell = (V_\ell, E_\ell)$이라 하고, 그 레이어드 네트워크는 $\hat{L_\ell} = (\hat{V_\ell}, \hat{E_\ell})$라 해보자. 다음의 과정을 통해 길이 $\ell$의 증가 경로를 따라 보낼 수 있는 유량을 모두 보낼 수 있다.

1. $\hat{L_\ell}$에서 증가 경로 $p$를 찾고, 흐름을 보낸다.
2. 그 다음 잔여 네트워크는 $G_{\ell'}$이라 하고, 그 최단 증가 경로의 길이도 $\ell$이라 하자. $G_{\ell'}$의 레이어드 네트워크 $\hat{L_{\ell'}}$은 $\hat{L_\ell}$에서 $p$의 핵심 간선이 삭제된 $\hat{L'_\ell}$의 부분집합이고, 따라서 $G_{\ell'}$의 증가 경로도 $\hat{L'_\ell}$에서 찾을 수 있다.
3. 또 다음 잔여 네트워크는 $G_{\ell''}$라 하고, 그 최단 증가 경로의 길이도 $\ell$이라 하자. $G_{l''}$의 증가 경로 $p''$도 마찬가지로 $\hat{L'_{\ell'}}$에서 찾을 수 있다. $\hat{L'_\ell}$에서 $p'$의 핵심 간선을 제거한 것을 $\hat{L''_\ell}$ 이라 하면, $\hat{L'_{\ell'}} \subseteq \hat{L''_\ell}$이므로 $p''$는 $\hat{L''_\ell}$에서 찾을 수 있다.
4. 마찬가지의 방법을 더 이상 길이 $\ell$의 증가 경로를 찾을 수 없을 때까지 반복한다.

데드엔드

하나 짚고 넘어가야 할 점은 $\hat{L_f}$에서 경로의 핵심 간선을 제거한 $\hat{L'_f}$는 레이어드 네트워크가 아닐 수 있다는 것이다. 레이어드 네트워크는 데드엔드(dead-end)가 없다는 성질을 가져야 한다.

데드엔드(dead-end)
$s$가 아닌 시작점이거나 $t$가 아닌 종료점인 정점. 다시 말해 $s$가 아니면서 자신으로 들어오는 간선이 없는 정점, 혹은 $t$가 아니면서 자신으로부터 나가는 간선이 없는 정점.

$\hat{L_f}$의 경우 $G_f$의 $s \rightarrow t$ 최단 경로를 모아 만들기 때문에 $s$가 아닌 시작점이나 $t$가 아닌 종료점이 존재하지 않지만, 이와 달리 $\hat{L'_f}$는 레이어드 네트워크인 $\hat{L_f}$에서 어떤 $s \rightarrow t$ 경로의 핵심 간선들을 삭제해 만들기 때문에, 핵심 간선들을 삭제하면서 몇 개의 데드엔드가 발생할 수 있다.

아래와 같은 $\hat{L_f}$가 있다고 하자. 간단하게, $s, t$를 제외한 각 레이어의 정점들은 말 그대로 바로 옆에 있는 한 정점으로의 간선만을 가진다고 해보자.

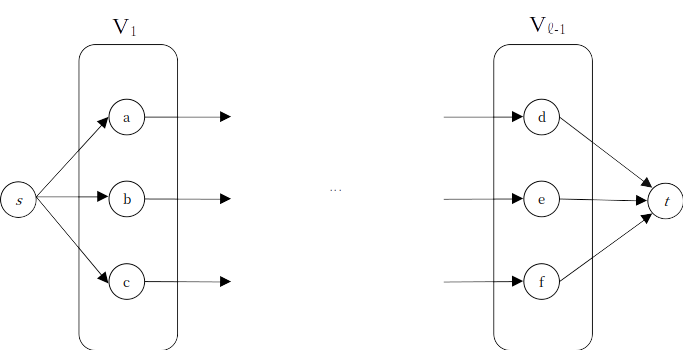
DFS를 통해 증가 경로를 찾았을 때, 간선 $(d, t)$가 핵심 간선이 되어 사라졌다고 하자. 정점 $d$는 데드엔드가 되었다.

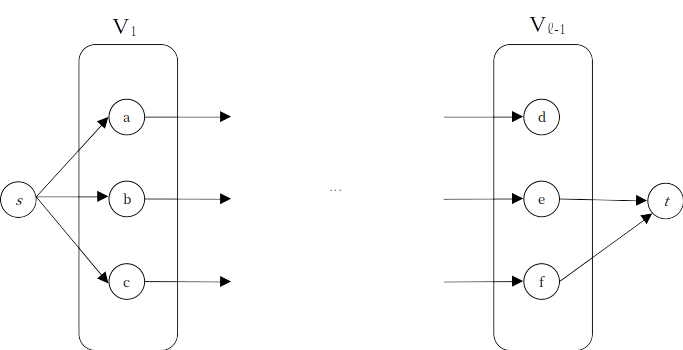
이제 다음 증가 경로를 찾아보자. DFS를 통해 $s \rightarrow a \rightarrow d$ 최단 경로를 따라 가다, $d$가 데드엔드임을 확인한다. 쭉 돌아와 $s \rightarrow b \rightarrow e \rightarrow t$ 경로를 최단 경로로 찾는다고 하자. 이 경로의 핵심 간선은 $(e, t)$였고, 흐름이 추가됨과 함께 사라진다. 이제는 $e$도 데드엔드다.

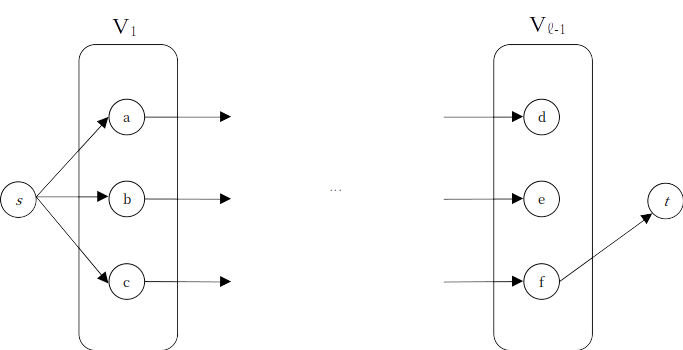
또 증가 경로를 찾으면 경로 $s \rightarrow a \rightarrow d$와 $s \rightarrow b \rightarrow e$를 탐색한 후, $s \rightarrow c \rightarrow f \rightarrow t$의 경로를 찾게 된다.

만약 데드엔드로 향하는 경로를 적절히 사라지게 했다면 어땠을까? $d$가 데드엔드가 됐을 때, $d$로 향하는 경로를 없애보자.

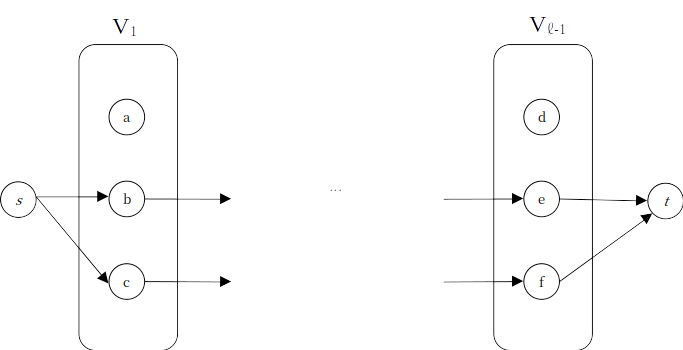
$s \rightarrow b \rightarrow e \rightarrow t$의 최단 경로를 곧바로 찾을 수 있다. 마찬가지로 $(e, f)$가 핵심 간선이라 $e$가 데드엔드가 됐다고 하자. $e$로 향하는 경로를 없애면,

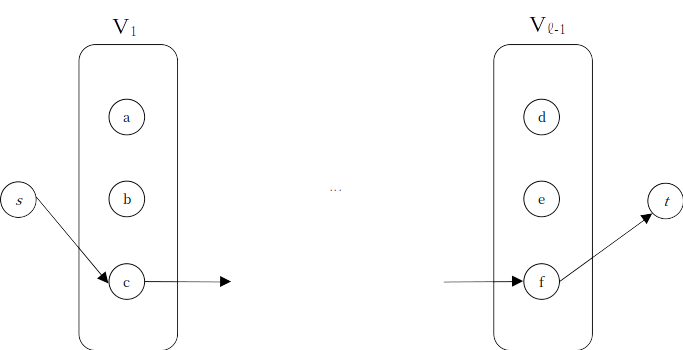
$s \rightarrow c \rightarrow f \rightarrow t$의 경로를 곧바로 찾을 수 있다.

사실 데드엔드가 남아있는 $\hat{L'_f}$를 그대로 사용하더라도 최단 경로는 (존재한다면) 반드시 찾을 수 있다. 하지만 데드엔드로의 경로를 매번 탐색하게 되면 시간복잡도가 어마무시하게 높아져버릴지도
모른다.

데드엔드를 삭제하는 과정은 다음과 같다. 유량 증가와 함께 간선 $(u, v)$가 삭제된다고 하자.

1. 만약 $u$로부터 나가는 간선이 더 이상 존재하지 않는다면, $u$는 데드엔드가 된다.
   • $u$가 데드엔드라면, $u$로 향하는 모든 간선들을 삭제하고, 해당 간선들에 대해서도 동일한 작업을 수행한다.
2. 마찬가지로 $v$로 들어오는 간선이 더 이상 존재하지 않는다면, $v$는 데드엔드가 된다.
   • $v$가 데드엔드라면 $v$로부터 나가는 모든 간선들을 삭제하고, 해당 간선들에 대해서도 동일한 작업을 수행한다.

이렇게 $\hat{L'_f}$로부터 발생할 수 있는 데드엔드로의 경로를 모두 삭제하면, $s \rightarrow t$ 최단 경로들에 포함되는 간선들만이 남게 되어 $G_{f'}$의 레이어드 네트워크 $\hat{L_{f'}}$이 된다.

(4) 최대 유량 찾기

이제 최대 유량을 찾아보자. 최대 유량을 반환할 때까지 아래를 반복한다.

1. BFS를 통해 잔여 네트워크 $G_f$에 대한 레이어드 네트워크 $\hat{L_f}$를 구성한다.
   • $s \rightarrow t$의 경로를 찾을 수 없다면, 더 이상 증가 경로가 없다는 뜻이므로, $|f|$를 반환하며 종료한다.
   • 그렇지 않은 경우 자료 구조 $L$에 $\hat{L_f}$를 넣는다.
2. $L$이 빌 때까지,
   1. $L$에서 $s \rightarrow t$ 최단 경로 $p$를 찾는다.
   2. $p$를 따라 유량을 보낸다.
   3. 더 이상 유량을 흘려 보낼 수 없게 된 $p$의 핵심 간선들을 $L$에서 삭제한다.
   4. $p$의 핵심 간선들을 삭제하면서 데드엔드가 되는 정점들이 있다면, 해당 정점으로의 경로가 존재하지 않도록 만든다.

시간복잡도

디닉 알고리즘의 각 페이즈를 종료하는 데 걸리는 시간은 $O(|V||E| + |E|) = O(|V||E|)$이다.

각 페이즈에서,

1. BFS를 통해 잔여 네트워크 $G_\ell$의 레이어드 네트워크 $\hat{L_\ell}$를 구성하는 데에는 $O(|E|)$의 시간이 걸린다.
2. $L$이 빌 때까지,
   1. $L$에서 $s \rightarrow t$ 최단 경로를 찾아 유량을 보내는 데에는 경로의 길이만큼의 시간이 걸린다. 경로의 길이는 길어봐야 $|V| - 1$이니 $O(|V|)$의 시간이 걸린다.
   2. $p$에서 핵심 간선은 많아봐야 경로의 길이만큼 있으니, 이를 제거하는 데에는 $O(|V|)$의 시간이 걸린다.
   3. 데드엔드로의 경로를 제거하는 데에는 $O(|E|)$의 시간이 걸린다.
      • $(u, v)$가 핵심 간선이면서 해당 레이어의 유일한 간선이라고 생각해보자. $(u, v)$를 삭제하는 순간 레이어드 네트워크의 모든 간선이 사라진다.

위 분석대로라면, 2번을 한 번 수행하는 데에는 최대 $O(|V| + |E|)$의 시간이 걸린다. 한 페이즈에서 증가 경로는 많아야 핵심 간선의 수만큼 있고, 핵심 간선은 많아야 $O(|E|)$개 있으므로, 2번은 $O(|E|)$번 반복될 수 있다. 따라서

디닉 알고리즘의 한 페이즈가 종료되는 데 걸리는 시간은 $O(|E| + |V||E| + |E|^2) = O(|E|^2)$다.

가 아니라, 사실 2-3에서 사라진 간선들은 이후 같은 페이즈의 반복에서는 다시 나타나지 않는다. 때문에 2-3은 한 페이즈 전체에서 많아봐야 $O(|E|)$번 수행될 수 있다. 그러므로 사실 한 페이즈를 종료하는 데 걸리는 시간은 $O(|E| + |V||E| + |E|^2)$가 아니라 $O(|E| + |V||E| + |E|) = O(|V||E|)$다.

디닉 알고리즘의 총 시간복잡도는 $O(|V|^2|E|)$다.

한 페이즈는 $s \rightarrow t$ 최단 경로의 길이가 같은 것들을 묶은 것이다. 이 경로의 길이는 길어봐야 $|V| - 1$이므로, 서로 다른 페이즈의 개수도 $O(|V|)$다.

한 페이즈가 종료되는 데 $O(|V||E|)$의 시간이 걸리니, $O(|V|)$개의 페이즈가 종료되기 위한 총 시간복잡도는 $O(|V|^2|E|)$다.

3. Shimon Even & Alon Itai의 구현

Shimon Even과 Alon Itai의 버전의 디닉 알고리즘은, 지금까지 이야기 해온 디니츠의 오리지널 버전과는 조금 차이가 있다. 가장 큰 차이는 $\hat{L}(s, t)$를 사용하지 않고 $L(s)$를 사용한다는 점이다.

오리지널 버전에서는 $s$에서 BFS를 수행해 $L(s)$를 만들고, 다시 $t$에서 BFS를 수행해 $s \rightarrow t$의 최단 경로만을 남겼다.

그런데 사실 꼭 $\hat{L}(s, t)$를 어떤 자료구조로 구현해야 할 필요는 없다. $s \rightarrow t$의 최단 경로 탐색이 가능하기만 하면 되고, 이는 $L(s)$만으로도 충분하다.

이 구현에서는 이미 증가 경로가 아님이 확인된 경로를 재탐색하지 않기 위한 백트래킹 테크닉을 하나 사용한다. 이를 이용하면 $L(s)$에 있는, $t$가 아닌 종점들로 향하는 경로를 탐색하는 일을 막을 수 있고, 또한 간선 삭제로 인해 발생하는 데드 엔드 경로도 굳이 삭제할 필요가 없어진다.

4. 코드(C++)

이번에는 2367번 파티를 디닉 알고리즘을 이용해 풀어보자. Shimon Even과 Alon Itai의 구현을 따른다.

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

#define fastio cin.tie(NULL); cout.tie(NULL); ios_base::sync_with_stdio(false)
#define all(v) v.begin(), v.end()

const int INF = 1e9;

struct Flow_Network{

	struct Edge {//간선
		int to;//어디로 가는 간선인지
		int capacity;//용량
		int flow;//흐름

		Edge(int _to, int _cap) : to(_to), capacity(_cap), flow(0) {}

		Edge *reverse;//역방향 간선

		void push(int f) {//(u,v)로 흐름 증가. 역방향 간선인 (v,u)에는 흐름 감소
			flow += f;
			reverse->flow -= f;
		}
	};

	vector<vector<Edge*>> edges;//한 정점으로부터 시작하는 간선들의 리스트
	vector<int> layer, work;//정점들이 속한 레이어, 가장 최근에 본 간선 인덱스
	int source = 0, sink = 0;

	Flow_Network(int N): source(0), sink(N + 1), edges(N + 2), layer(N + 2), work(N + 2) {}

	void add_edge(int u, int v, int c) {//용량이 c인 간선 (u, v)
		Edge *edge = new Edge(v, c);//v로 향하는 용량 c의 간선
		Edge *reverse_edge = new Edge(u, 0);//역방향 간선 (v, u)

		//두 간선의 역방향 관계 설정
		edge->reverse = reverse_edge;
		reverse_edge->reverse = edge;

		edges[u].emplace_back(edge);//정점 u에 간선을 추가
		edges[v].emplace_back(reverse_edge);//정점 v에 간선을 추가
	}

	bool find_vertex_layer() {//레이어드 네트워크 L(s)의 정점 레이어 구성
		queue<int> q;
		q.push(source);

		fill(all(layer), -1);//미방문한 정점 표시
		layer[source] = 0;//소스는 V_0에 속함.

		//BFS를 통한 레이어드 네트워크 구성
		while (!q.empty()) {
			int from = q.front();
			q.pop();

			for (auto &edge: edges[from]) {//연결된 간선들을 보면서
				int to = edge->to;
				if (layer[to] != -1) continue;//방문한 정점인 경우는 제외
				if (edge->capacity - edge->flow > 0) {//잔여 용량이 있는 경우
					q.push(to);//큐에 추가
					layer[edge->to] = layer[from] + 1;//d(v) = d(u) + 1
				}
			}
		}

		return layer[sink] != -1;//싱크에 방문하지 못했다면 더 이상 증가 경로를 찾을 수 없음.
	}


	int augment_flow(int cur, int flow) {//증가 경로를 찾고 해당 경로로 보낼 수 있는 흐름을 찾아 보냄
		if (cur == sink) return flow;

		//현재 정점과 연결된 간선들을 보되, 이미 지나간 건 다시 볼 필요가 없음.
		for (int &i = work[cur]; i < edges[cur].size(); i++) {
			Edge *edge = edges[cur][i];
			int to = edge->to;
			int residual_capacity = edge->capacity - edge->flow;

			if (layer[to] != layer[cur] + 1) continue;//L_f에 포함된 간선이 아니면 제외
			if (residual_capacity <= 0) continue;//잔여 용량이 없으면 제외

			//이후 t로의 경로에 흘려보낼 수 있는 흐름을 찾기
			int f_p = augment_flow(to, min(flow, residual_capacity));

			if (f_p > 0) {//보낼 수 있다면
				edge->push(f_p);//보냄
				return f_p;
			}
		}
		return 0;
	}

	int dinic() {
		int max_flow = 0;//최대 유량

		while (find_vertex_layer()) {//s->t 최단 경로를 찾을 수 있나?
			//최단 경로가 존재한다면

			fill(all(work), 0);//각 정점에서 최근에 본 간선 인덱스를 0으로 설정 
		
			while (true) { 
				//증가 경로를 찾고, 해당 경로로 보낼 수 있는 흐름을 찾아 보냄.
				int f = augment_flow(source, INF);

				//최대 유량 추가
				max_flow += f;
		
				//더 이상 보낼 수 없다면 정지
				if (!f) break;
			}
		}

		return max_flow;
	}
};

int main() {
	fastio;

	int N, K, D;
	cin >> N >> K >> D;

	Flow_Network network(N + D);

	for (int i = 1; i <= D; i++) {
		int M;
		cin >> M;
		network.add_edge(N + i, network.sink, M);
	}

	for (int i = 1; i <= N; i++) {
		network.add_edge(network.source, i, K);

		int Z;
		cin >> Z;

		for (int j = 0; j < Z; j++) {
			int food;
			cin >> food;
			network.add_edge(i, N + food, 1);
		}
	}

	cout << network.dinic();
}

main은 이전과 동일하다. struct Flow_Network 내부만 보자.

struct Edge

struct Edge {//간선
	int to;//어디로 가는 간선인지
	int capacity;//용량
	int flow;//흐름

	Edge(int _to, int _cap) : to(_to), capacity(_cap), flow(0) {}

	Edge *reverse;//역방향 간선

	void push(int f) {//(u,v)로 흐름 증가. 역방향 간선인 (v,u)에는 흐름 감소
		flow += f;
		reverse->flow -= f;
	}
};

Edge는 간선을 담기 위한 구조체다. $(u, v)$ 간선이라고 한다면, 이 간선은 edges[u]에 to = v인 간선을 추가한다. push()를 통해 $(u, v)$ 간선을 따라 흐름을 보낸다.

add_edge()

void add_edge(int u, int v, int c) {//용량이 c인 간선 (u, v)
		Edge *edge = new Edge(v, c);//v로 향하는 용량 c의 간선
		Edge *reverse_edge = new Edge(u, 0);//역방향 간선 (v, u)

		//두 간선의 역방향 관계 설정
		edge->reverse = reverse_edge;
		reverse_edge->reverse = edge;

		edges[u].emplace_back(edge);//정점 u에 간선을 추가
		edges[v].emplace_back(reverse_edge);//정점 v에 간선을 추가
	}

크게 볼 것은 없다.

dinic()

int dinic() {
	int max_flow = 0;//최대 유량

	while (find_vertex_layer()) {//정점 레이어를 구성

		fill(all(work), 0);//각 정점에서 최근에 본 간선 인덱스를 0으로 설정 
	
		while (true) { 
			//증가 경로를 찾아 해당 경로로 보낼 수 있는 흐름을 찾아 보낸다.
			int f = augment_flow(source, INF);

			//최대 유량 추가
			max_flow += f;
	
			//더 이상 보낼 수 없다면 정지
			if (!f) break;
		}
	}

	return max_flow;
}

find_vertex_layer()

bool find_vertex_layer() {//레이어드 네트워크 L(s)의 정점 레이어 구성
	queue<int> q;
	q.push(source);

	fill(all(layer), -1);//미방문한 정점 표시
	layer[source] = 0;//소스는 V_0에 속함.

	//BFS를 통한 레이어드 네트워크 구성
	while (!q.empty()) {
		int from = q.front();
		q.pop();

		for (auto &edge: edges[from]) {//연결된 간선들을 보면서
			int to = edge->to;
			if (layer[to] != -1) continue;//방문한 정점인 경우는 제외
			if (edge->capacity - edge->flow > 0) {//잔여 용량이 있는 경우
				q.push(to);//큐에 추가
				layer[edge->to] = layer[from] + 1;//d(v) = d(u) + 1
			}
		}
	}

	return layer[sink] != -1;//싱크에 방문하지 못했다면 더 이상 증가 경로를 찾을 수 없음.
}

BFS를 통해 레이어드 네트워크 $L_f(s)$의 정점 레이어를 구성한다. 소스부터 시작해 연결된 각 간선들을 본다. 미방문한 정점인 경우, 잔여 용량이 있는지 확인한다. 잔여 용량이 있다면 큐에 추가하고, 해당 정점이 어떤 레이어에 속하는지를 기록한다.

만약 layer[sink] == -1이라면 더 이상 싱크로의 경로가 존재하지 않는다는 것, 즉 더 이상의 증가 경로가 없다는 말이다. 여기서 디닉 알고리즘은 종료된다.

$G_f$의 $s \rightarrow t$ 최단 경로들을 담은 $\hat{L_f}(s, t)$가 아니라, $s$에서 모든 정점으로의 최단 경로를 담은 $L_f(s)$다.

augment_flow()

int augment_flow(int cur, int flow) {//증가 경로를 찾고 해당 경로로 보낼 수 있는 흐름을 찾아 보냄
	if (cur == sink) return flow;//싱크인 경우는 종료한다.

	//현재 정점과 연결된 간선들을 보되, 이미 지나간 건 다시 볼 필요가 없음.
	for (int &i = work[cur]; i < edges[cur].size(); i++) {
		Edge *edge = edges[cur][i];
		int to = edge->to;
		int residual_capacity = edge->capacity - edge->flow;

		if (layer[to] != layer[cur] + 1) continue;//L_f(s)에 포함된 간선이 아니면 제외
		if (residual_capacity <= 0) continue;//잔여 용량이 없으면 제외

		//이후 t로의 경로에 흘려보낼 수 있는 흐름을 찾기
		int f_p = augment_flow(to, min(flow, residual_capacity));

		if (f_p > 0) {//보낼 수 있다면
			edge->push(f_p);//보냄
			return f_p;
		}
	}
	return 0;
}

증가 경로를 찾고 해당 경로로 흐름을 보내는 함수다. 파라미터 flow는 현재 정점 cur까지의 경로에서 흐를 수 있는 흐름으로, 초기값은 INF로 둔다.

현재 보고 있는 정점과 연결된 간선들을 보자. 해당 간선을 $(cur, to)$라 할 때, 이 $L_f(s)$에 포함된 간선인지는 layer[to] = layer[cur] + 1인지, 그리고 잔여 용량이 남아있는지를 통해 확인할 수 있다. 만약 그렇다면 flow와 간선의 잔여 용량 중 작은 것을 이후 경로로 흘려보내기를 시도할 수 있다.

DFS가 $\hat{L_f}$가 아닌 $L_f$ 위에서 수행되므로, $t$가 아닌 다른 정점이 DFS의 종점이 되는 경우가 발생할 수 있다. 이 경우에는 아래에서 $0$이 반환되기에 걸러진다.

눈여겨 볼 것은 vector<int> work를 통해 이미 본 탐색했던 간선들을 스킵하는 테크닉이다. 위 for문에서 i가 증가하는 경우는 edges[cur][i]에 해당하는 간선을 지났을 때 $t$로의 증가 경로를 찾지 못하는 경우 밖에 없다. 이 정보를 work[cur]에 저장해둔다면, $t$로의 증가 경로가 존재하지 않는 것이 확실한 간선들에 대한 탐색을 걸러낼 수 있기에 실행 시간을 훨씬 줄일 수 있다.

References

• Dinitz, Yefim. (2006). Dinitz’ Algorithm: The Original Version and Even’s Version. 218-240. 10.1007/11685654_10.
• https://gazelle-and-cs.tistory.com/84