Operating Systems : Three Easy Pieces를 보고 번역 및 정리한 내용들입니다.

5. RAID Level 1: Mirroring

스트라이핑 다음의 첫 번째 RAID 레벨은 RAID 레벨 1, 또는 미러링이라 불린다. 미러링된 시스템에서는 시스템 내의 각 블럭에 대해 적어도 하나 이상의 복사본을 만들어 별도의 디스크에 배치함으로써 디스크 결함을 감내한다.

전형적인 미러링 시스템에서, 각 논리적 블럭에서 RAID가 해당 블럭의 두 물리적 복사본을 가진다고 가정한다. 예는 다음과 같다.

예에서 디스크 0, 1은 동일한 내용을 가지고 있고, 디스크 2와 3도 그렇다. 데이터들은 이 미러링된 쌍들에 걸쳐 스트라이핑 되어 있다. 사실 블럭 복사본들을 디스크에 걸쳐 복사하는 방식에는 여러 방법이 있을 수 있다. 위와 같은 배치는 일반적인 방법으로, RAID-10(또는 RAID 1+0, stripe of mirrors)이라 불린다. 왜냐하면 미러링된 쌍(RAID-1)을 쓰면서 그 위에 스트라이핑(RAID-0)을 함께 쓰고 있기 때문이다. 다른 일반적인 배치 방식에는 RAID-01(또는 RAID 0+1, mirror of stripes)이 있다. 지금은 전자와 같은 레이아웃을 사용한다고 가정한다.

블럭을 미러링된 배열에서 읽을 때 RAID는 어떤 복사본으로부터 읽을지를 선택해야한다. 예를 들어 논리 블럭 5에 대한 읽기 요청이 RAID에 발생하면, 이는 디스크 2, 3번 중 어느 것으로부터든 읽을 수 있다. 한편 읽기의 경우에는 그렇지 않다. RAID는 신뢰성을 유지하기 위해 두 데이터 복사본을 모두 업데이트 해야하기 떄문이다. 다만 이 쓰기 작업이 병렬적으로 일어날 수 있다는 것에 유의하자. 5번 논리 블럭에 대한 쓰기 작업은 디스크 2, 3번에 동시에 일어날 수 있다.

RAID-1 Analysis

RAID-1을 평가해보자. 용량의 측면에서 보자면 RAID-1은 비싸다. 미러링 레벨이 2일 때에는 전체 용량의 반 밖에 사용할 수 없게 된다. $B$개의 블럭을 가지는 $N$개의 디스크에 대해, RAID-1의 사용 가능한 용량은 $(N \cdot B) / 2$ 밖에 되지 않는다.

RAID-1은 신뢰성의 측면에서는 좋다. 이는 어떤 한 디스크에서 일어나는 결함을 감내할 수 있다. 운이 좋다면 RAID-1이 그보다도 더 잘 할 수 있다는 것도 알 수 있을 것이다. 위와 같은 상황에서 디스크 0과 2가 모두 고장이 난 경우를 생각해보자. 그런 상황에서도 데이터 손실은 일어나지 않는다. 더 일반적으로 미러링된 시스템은 하나의 디스크 고장은 반드시 감내할 수 있고, 어떤 디스크가 고장이 났는지에 따라서는 $N/2$개의 디스크 고장도 감내할 수 있다. 물론 실무에서는 이렇게 $N/2$개의 디스크가 고장나는 상황을 운에 맡겨두고 싶지는 않을 것이기에, 대부분의 사람들은 미러링이 단일한 디스크의 고장을 다루는 데에 좋다고 생각한다.

마지막으로는 성능을 분석해보자. 한 읽기 요청의 지연에 대한 관점에서 보면, RAID-1의 지연은 한 디스크에서와 같다. RAID-1이 하는 것은 읽기 작업을 복사본 중 하나로 요청을 전달하는 것 뿐이기 때문이다. 한편 쓰기 작업의 경우에는 조금 다르다. 하나의 논리적 쓰기 작업이 완료되기 위해서는 두 번의 물리적 쓰기 작업이 필요하기 때문이다. 이 두 쓰기 작업이 병렬적으로 일어나기에, 쓰기 시간은 대충 한 번의 쓰기 시간과 같다. 하지만 논리적 쓰기는 두 물리적 쓰기가 완료될 때까지, 따라서 두 요청에 각각에 걸리는 탐색 시간 및 회전 지연 중 최악의 경우 만큼 대기해야 한다. 따라서 평균적으로는 단일 디스크에 쓰는 것보다는 좀 더 느리다.

정상 상태 처리량을 분석하기 위해, 우선은 순차 워코로드부터 시작해보자. 디스크에 순차적으로 쓰기 위해서, 각 논리적 쓰기는 두 번의 물리 쓰기로 이어진다. 예를 들어 논리 블럭 0번에 써야할 때, RAID는 내부적으로 디스크 0, 1번에 써야 한다. 그러므로 미러링된 배열에의 쓰기 작업에서 얻을 수 있는 최대 대역폭은 $(\frac{N}{2} \cdot S)$, 또는 최대 대역폭의 절반이다.

불행하게도, 순차적 읽기의 성능도 마찬가지다. 저장된 데이터를 모두 읽지 않고 둘 중 하나만 읽어야하기 때문에 순차적 쓰기보다는 상황이 나을 것이라 생각할 수도 있겠다. 왜 그렇지 않은지를 한 번 살펴보자. 논리 블럭 0에서 7까지에 대한 순차적 읽기 요청이 발생했고, RAID가 각각의 데이터를 0, 2, 1, 3, 0, 2, 1, 3번 디스크로부터 가져오도록 결정했다고 해보자. 단순하게 이때 모든 디스크들을 활용하고 있으므로, 배열의 최대 대역폭을 달성할 수 있을 것이라 생각할 수도 있다.

하지만 한 디스크가 받는 요청들을 생각해보자. 디스크 0은 우선 블럭 0에 대한 요청을 받고, 블럭 2를 건너뛰고 블럭 4에 대한 요청을 받는다. 사실 각 디스크는 단일 디스크의 경우에서는 연속적으로 처리했을 블럭들은 건너뛰고 다음의 블럭에 대한 요청을 받게 된다. 이때 스킵된 블럭을 지나 회전을 하기는 하지만, 이는 클라이언트에게 유용한 대역폭을 가져다 주지는 않는다. 따라서 순차 읽기의 경우 각 디스크는 최대 대역폭의 반, 즉 $(\frac{N}{2} \cdot S)$ MB/s밖에 얻지 못한다.

랜덤 읽기는 미러링된 RAID의 최고의 경우다. 이 경우에는 읽기 작업을 디스크에 걸쳐 분산시킬 수 있고, 가능한 최대 대역폭을 얻을 수 있다.

한편 랜덤 쓰기는 $\frac{N}{2} \cdot R\ MB/s$의 성능을 가진다. 각 논리적 읽기는 두 물리적 쓰기로 변하고, 따라서 모든 디스크들이 사용되고 있어도 클라이언트는 사용 가능한 대역폭의 절반만을 사용할 수 있게 된다. 논리 블럭 $x$에 대한 쓰기가 서로 다른 두 물리 블럭에 대한 병렬적 쓰기로 전환되더라도, 수많은 작은 요청으로는 스트라이핑에서 얻을 수 있는 대역폭의 절반 밖에 얻지 못한다. 다만 사실 이렇게 가능한 대역폭의 절반을 얻는 것은 꽤 좋은 결과이기는 하다.

6. RAID Level 4: Saving Space With Parity

이번에는 패리티(parity)를 통해 디스크 배열에 데이터 중복을 추가하는 방법에 대해 알아보자. 패리티 기반 방식은 적은 용량을 사용함으로써 미러링된 시스템에서의 공간적 대가 문제를 극복한다. 다만 패리티 기반 방식은 그 대가로 성능을 지불한다.

위는 다섯 개의 디스크를 사용하는 RAID-4의 예시다. 각 데이터의 스트라이프에는 하나의 패리티 블럭을 추가하는데, 이 블럭에는 해당 스트라이프 내 블럭들에 대한 데이터 중복 정보를 저장한다. 예를 들어 패리티 블럭 P1은 블럭 4, 5, 6, 7로부터 계산된 중복 데이터 정보를 담고 있다.

패리티를 계산하기 위해서는 해당 스트라이프에서 한 블럭에서의 데이터 손실이 일어난 경우를 알 수 있게 하기 위한 수학적 함수가 필요하다. 간단한 XOR 함수가 이 역할을 꽤 잘 수행한다. 주어진 비트 집합이 있을 때, XOR은 해당 집합에 있는 1의 개수가 짝수면 0, 그 외의 경우에는 1을 반환한다. 다음과 같은 예를 보자.

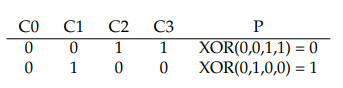
첫 번째 행에서는 1이 두 개 있어 XOR 결과는 0이 되고, 두 번째 행에서는 1이 하나 있어 XOR 결과는 1이 된다. 간단하게는, 어떤 행에 있든 패리티 비트를 포함한 1의 개수가 홀수가 아닌 짝수가 되어야 한다고 기억하면 된다. 이것은 패리티가 제대로 동작하기 위해 RAID가 유지해야 하는 불변량(invariant)이다.

위의 예에서 어떻게 패리티 비트를 이용해 결함 상태로부터 복구할 수 있는지에 대해서도 궁금할 수 있을 것이다. C2 컬럼이 손실되었다고 생각해보자. 이 컬럼에 어떤 값이 있었는지를 알기 위해서는, 해당 행의 다른 값들을 모두 읽고 정답을 재구축하면 된다. 구체적으로, C2의 첫 번째 행의 값이 손실되었다고 해보자. 해당 행의 C0, C1, C3, P 열의 다른 값들을 읽어보면 0, 0, 1, 0이다. XOR은 해당 행의 1의 수를 짝수로 유지하므로, 사라진 데이터는 1이 되어야 한다. 이것이 XOR 기반 패리티 기법에서의 값 재구축 방식이다. 또한 어떻게 재구축된 값을 계산했는지에 대해서도 주의하자. 처음에 패리티를 계산할 때와 마찬가지로, 남은 데이터 비트들과 패리티 비트를 XOR 연산함으로써 손실된 열의 기존값을 재구축 한 것이다.

그런데 다음과 같은 사실이 궁금할 수도 있다. 지금까지는 각 열의 비트들을 XOR 연산헀지만, 우리는 RAID가 4KB, 혹은 그보다 큰 블럭들을 디스크에 가지고 있음을 알 수 있다. 어떻게 이 블럭 다발을 이용해서 패리티를 계산할 수 있을까? 이것도 사실 쉽다. 데이터 블럭의 각 비트마다 XOR 연산을 수행하면 되는 것이다. 각 블럭의 각 비트끼리 연산한 결과는 패리티 블럭의 해당 비트 자리의 값이 된다. 예를 들면 이번에는 4비트 사이즈의 블럭을 가지고 있다고 해보자. 그러면 다음과 같이 생겼을 것이다.

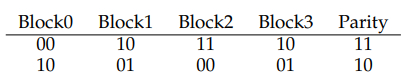
여기서 볼 수 있듯, 패리티는 각 블럭의 각 비트끼리 계산한 결과를 패리티 블럭의 해당 비트 자리에 넣음으로써 계산된다.

RAID-4 Analysis

이제는 RAID-4를 분석해보자. 용량의 측면에서 RAID-4는 패리티 정보를 이용해 보호할 디스크 그룹들을 위해 한 디스크를 패리티 디스크로 사용한다. 그러므로 사용 가능한 용량은 $(N-1) \cdot B$이 된다.

신뢰성도 꽤 이해하기 쉽다. RAID-4는 단 하나의 디스크 결함을 감내한다. 만약 하나보다 많은 디스크에 손실이 나는 경우에는 손실된 데이터를 재구축할 방법이 전혀 없다.

마지막으로 성능을 보자. 이번에는 정상 상태 처리량을 우선 계산해보자. 순차 읽기의 경우 패리티 디스크를 제외한 모든 디스크들을 활용하므로, 최대 대역폭은 $(N-1) \cdot S$ MB/s가 된다.

순차 쓰기의 성능을 분석하기 위해서는 해당 작업이 어떻게 이루어지는지를 알아야 한다. 큰 데이터 청크를 디스크에 쓸 때, RAID-4는 full-stripe write라 불리는 간단한 최적화를 수행한다. 예를 들어 블럭 0, 1, 2, 3이 쓰기 요청의 일부로서 RAID로 보내진 경우를 생각해보자.

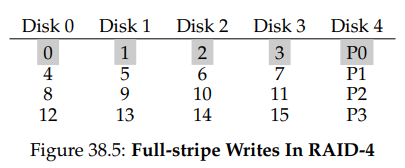
이 경우 RAID는 새값 P0을 간단히 계산하고 위 다섯 디스크의 블럭들 전부에 병렬적으로 쓸 수 있다. 그러므로 full-stripe write는 RAID-4가 디스크에 쓰는 가장 효율적인 방식이다.

full-stripe write에 대해 이해한다면 RAID-4에서의 순차 쓰기 성능을 이해하는 일은 쉽다. 여기서의 유효 대역폭은 마찬가지로 $(N-1) \cdot S$ MB/s다. 비록 패리티 디스크가 쓰기 작업 중에 계속해서 쓰이고는 있지만, 클라이언트는 이로부터 어떤 성능 향상도 얻지 못한다.

이번에는 랜덤 읽기의 성능을 분석해보자. 위 표에서 볼 수 있듯, 1-블럭 랜덤 읽기의 집합은 패리티 디스크를 제외한 시스템의 데이터 집합에 퍼져있다. 따라서 유효 성능은 $(N-1) \cdot R$ MB/s다.

마지막으로 랜덤 쓰기는 RAID-4에서 가장 흥미로운 경우다. 위 블럭 1에 덮어쓰려 한다고 해보자. 이 경우 그냥 가서 덮어 쓰면 되겠지만, 이때는 패리티 블럭 P0이 스트라이프의 올바른 패리티 값을 정확히 반영하지는 못한다는 문제가 발생한다. 즉 P0도 업데이트 돼야 한다. 그렇다면 올바르게, 그리고 효율적으로 패리티 값을 업데이트하는 방법은 무엇일까?

그 방법에는 두 가지가 있는데, 첫 번째는 가산 패리티(additive parity)다. 가산 패리티에서 새로운 패리티 블럭의 값을 계산하기 위해 스트라이프의 모든 다른 데이터 블럭들을 병렬적으로 읽고 업데이트 된 새 데이터 블럭과 XOR연산하는 것이다. 이때 결과는 당연히 새 패리티 블럭의 값이 될 것이다. 이렇게 한 후에야 새 데이터와 패리티를 해당하는 각 블럭에 병렬적으로 쓴다.

이 방법에서의 문제는 디스크의 수가 많아짐에 따라 RAID가 패리티를 계산하기 위해 읽어야 하는 수도 많아진다는 것이다. 그러므로 다음의 감산 패리티(subtractive parity)를 사용한다.

예를 들어 다음과 같이 비트 스트링을 생각해보자. 데이터 비트로 4개, 패리티 비트로 하나가 있다.

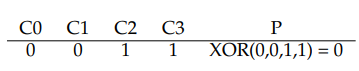
이제 C2를 새로운 값으로 덮어 쓰려한다 해보자. 이 값을 C2$_{new}$라 부른다. 감산법은 다음의 세 단계로 동작한다. 우선 C2의 옛 값(C2$_{old})$과 패리티의 옛 값(P$_{old}$)를 읽는다. 다음으로는 오래된 데이터와 새 데이터를 비교한다. 만약 두 데이터가 같다면 패리티 비트는 그대로 유지될 것이다. 하지만 만약 두 데이터의 값이 다르면 오래된 패리티를 현재 상태의 반대로 바꿔야 한다. 즉 만약 (P$_{old}$ == 1)이면 P$_{new}$는 0이 될 것이고, 반대의 경우에는 1이될 것이다. 이 과정을 다음과 같이 간단하게 표현할 수 있다.

우리는 비트가 아니라 블럭을 다뤄야 하므로, 이 연산을 블럭의 모든 비트에 대해 수행해야한다. 그러므로 대부분의 경우, 새 블럭은 옛 블럭과 달라질 것이고, 패리티 블럭도 마찬가지로 새 값을 가지게 될 것이다.

그렇다면 언제 가산 패리티를 사용하고, 언제 감산 패리티를 사용해야할까? 가산법을 사용할 때 감산법을 사용하는 것보다 적은 I/O 연산이 일어나기 위한 디스크의 수는 얼마나 돼야할지를 생각해보자.

성능 분석을 위해서는 감산법을 사용한다고 가정하자. 따라서 각 쓰기 작업마다 RAID는
쓰기 2번, 읽기 2번, 총 4번의 물리 I/O를 수행한다. RAID에 많은 쓰기 작업이 일어났을 때, 병렬적으로 처리할 수 있는 쓰기에는 얼마나 있을까? 다시 RAID-4 레이아웃을 살펴보자.

RAID-4에 블럭 4, 13에 대한 쓰기 작업이 동시에 요청되었다고 해보자. 해당 데이터는 디스크 0, 1에 있고, 따라서 읽기와 쓰기는 모두 병렬적으로 일어날 수 있다. 하지만 문제는 패리티 디스크다. 두 요청은 모두 각각 4, 13번 블럭과 연관된 패리티 블럭 1, 3번을 읽어야 한다. 이러한 종류의 워크로드에서 패리티 디스크는 병목 현상의 주범이 된다. 이러한 문제를 가리켜 패리티 기반 RAID의 small-write problem이라 부른다. 그러므로 데이터 디스크가 병렬적으로 접근될 수 있다 하더라도, 패리디 디스크는 어떠한 종류의 병렬성도 허용하지 않는다. 시스템에의 모든 쓰기 작업은 패리티 디스크로 인해 직렬화된다. 패리티 디스크는 논리 I/O 한 번마다 쓰기와 읽기, 총 두 번의 I/O를 수행하므로 RAID-4의 작은 랜덤 쓰기 작업의 성능은 패리티 디스크의 해당 두 I/O 작업에 대한 성능을 통해 계산할 수 있으며, 그 결과는 $(R/2)$ MB/s다. 작은 랜덤 쓰기에 대한 RAID-4의 작업량은 매우 낮다. 디스크를 시스템에 추가하더라도 성능의 개선을 가져오지 못하게 된다.

RAID-4에서의 I/O 지연을 분석하면서 마치도록 하자. 결함이 없는 경우 하나의 읽기 작업은 하나의 디스크로 전달되므로, 그 지연은 한 디스크 요청의 지연과 같다. 쓰기 작업 하나의 지연은 두 번의 읽기와 두 번의 쓰기를 필요로 하는데, 읽기는 읽기끼리, 쓰기는 쓰기끼리 병렬적으로 수행될 수 있으므로 총 지연은 단일 디스크의 두 배가 될 것이다. 단 두 읽기가 끝나기를 기다려야하므로 최악의 접근 시간을 가지는 한편, 업데이트의 경우에는 탐색 비용이 들지 않아 평균 접근 시간보다는 더 나을 것이다.

7. RAID Level 5: Rotating Parity

small-write 문제를, 적어도 부분적으로 해결하기 위해, Patterson, Gibson, Katz는 RAID-5를 도입했다. RAID-5는 RAID-4와 거의 동일한 방식으로 동작하는데, 패리티 블럭을 드라이브에 걸쳐 순환(rotate)시킨다는 점만 제외하면 그렇다.

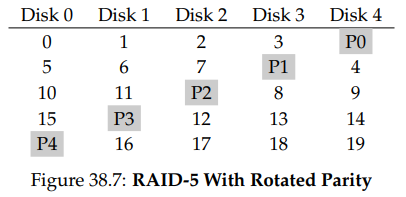
여기서 볼 수 있듯, 각 스트라이프의 패리티 블럭은 RAID-4의 패리디 디스크 병목 현상을 없애기 위해 디스크를 순환한다.

RAID-5 Analysis

RAID-5에 대한 분석은 거의 RAID-4와 비슷하다. 예를 들어 두 레벨의 유효 용량과 내결함성은 동일하다. 순차 읽기와 쓰기 성능도 그렇다. 쓰기든 읽기든 단일 요청의 지연시간도 RAID-4와 동일하다.

랜덤 읽기 성능은 조금 더 낫다. 왜냐하면 이제는 모든 디스크를 활용할 수 있기 때문이다. 마지막으로 랜덤 쓰기 성능은 RAID-4에 비해 훨씬 개선된다. 왜냐하면 요청 간의 병렬 처리가 가능해졌기 때문이다. 블럭 1과 블럭 10에 쓰는 경우를 생각해보자. 이는 디스크 1, 4, 그리고 디스크 0, 2의 쓰기로 바뀐다. 그러므로 이들은 모두 병렬적으로 수행될 수 있다. 사실 많은 양의 랜덤 요청이 주어진다면, 모든 디스크들을 거의 동등하게 사용할 수 있다고 가정할 수있다. 만약 그렇다면 이 작은 쓰기들에 대한 총 대역폭은 $\frac{N}{4} \cdot R$ MB/s가 된다. 이렇게 4로 나눈 이유는 각 RAID-5 쓰기가 여전히 총 4번의 I/O 작업을 만들기 때문이다. 이는 패리티 기반 RAID에서는 기본적으로 지불되는 비용이다.

RAID-5는 좀 더 잘 동작하는 몇 가지 경우를 제외하고는 기본적으로 RAID-4와 같고, 따라서 시장에서는 RAID-5가 RAID-4를 거의 완전히 대체하고 있다. 그렇지 않은 경우는 오직 large-write만 일어나서 small-write가 일어나지 않는 경우 뿐이다. 그런 경우 RAID-4는 만들기 조금 더 쉽다는 이유로 가끔 쓰이기도 한다.

8. RAID Comparison: A Summary

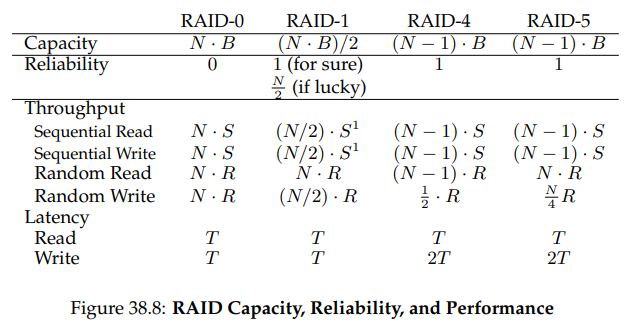
지금까지의 논의는 위와 같이 정리할 수 있다. 다만 분석을 단순화하기 위해 많은 세부 사항들을 생략했다는 것을 잊지 말자. 예를 들어 미러링된 시스템에서의 쓰기가 일어날 때의 평균 탐색 시간은 단일 디스크에의 쓰기 시간에서보다 조금 더 오래 걸린다. 이때의 탐색 시간은 두 탐색 중 최댓값이 되기 때문이다. 따라서 랜덤 쓰기 성능은 단일 디스크의 경우보다 조금 더 낮다. 또한 RAID-4/5에서 패리티 디스크를 업데이트 할 때, 오래된 패리티를 처음으로 읽을 때에는 최대 탐색 시간 및 회전 지연이 일어날 수 있지만, 두 번째 패리티 쓰기에서는 회전 지연만 일어난다. 마지막으로 미러링된 RAID에서의 순차 I/O는 다른 방식들에 비해 두 배 정도의 성능 패널티를 지불한다.

하지만 위 표에서의 비교는 근본적인 차이만 포착하고 있고, 따라서 RAID 레벨들 사이의 트레이드-오프를 이해하는 데에 유용하다. 지연 시간 분석을 위해서는 $T$를 이용해 간단하게 단일 디스크의 요청 처리 시간을 나타내고 있다.

오직 성능만 중요하고 신뢰성은 문제가 되지 않는 경우라면 스트라이핑이 최선이고, 만약 랜덤 I/O의 성능과 신뢰성이 문제라면 미러링이 최선이다. 물론 후자의 경우 그 대가는 용량이다. 만약 용량과 신뢰성이 핵심 목표라면, RAID-5가 최선이다. 이때의 비용은 small-write 성능이다. 항상 순차 I/O만을 수행하고 용량을 최대화하고 싶은 경우에도 RAID-5가 고를 만한 선택지일 것이다.

9. Other Interesting RAID Issues

RAID와 관련해 논의해 볼만한 흥미로운 아이디어들이 있다.

예를 들어, 원래의 분류에 따르면 RAID 레벨 2와 3도 있고, 다수의 디스크 결함을 감내하기 위한 레벨 6도 있다. 또한 디스크 고장이 일어났을 때 RAID가 무엇을 하는지도 있다. 때때로 RAID는 고장 난 디스크를 대체하기 위한 hot-spare를 미리 준비해놓는다. 결함이 일어났을 때 성능에는 어떤 일이 일어날까? 고장난 디스크를 재구축할 때에는 성능에 어떤 영향이 갈까? latent-sector-error나 block-corruption을 다루기 위한 더 현실적인 폴트 모델들도 있고, 그런 결함들을 해결하기 위한 많은 테크닉들도 있다. 마지막으로 RAID는 소프트웨어 계층에서 만들 수도 있다. 그런 소프트웨어 RAID 시스템은 좀 더 값싸지만, 일관적-업데이트 문제를 포함한 다른 문제들을 가지고 있다.

10. Summary

지금까지 RAID에 대해 논의해왔다. RAID는 여러 개의 독립적인 디스크를 하나의, 더 큰 용량을 가지며 더 신뢰성이 높은 독립체로 만든다. 더 중요한 것은 이것이 투명하게 이루어져, 그 위의 하드웨어와 소프트웨어는 상대적으로 그런 변화를 신경 쓸 필요가 없다는 점이다.

고를 수 있는 RAID 레벨에는 여러가지가 있고, 정확히 어떤 RAID 레벨을 사용할지는 최종 사용자가 무엇을 가장 중요하게 생각하는지에 달려 있다. 예를 들어 미러링된 RAID는 간단하고, 신뢰성 높고, 좋은 성능을 제공하지만 용량 비용도 높다. RAID-5는 반대로 신뢰성도 높고, 용량의 측면에서도 낫지만, 워크로드에 다수의 small-write가 포함된 경우에는 낮은 성능을 가진다. 특정 워크로드를 위해 적절하게 RAID를 고르고 파라미터를 설정하는 일은 어렵고, 과학보다는 예술의 영역으로 남아있다.