[CS234] - Lecture 2 - Given a Model of the World

용어정리

• Model: dynamics과 reward의 수학적 모델
• Policy: 주어진 state에서 action을 결정하는 함수
• Value function: 특정 policy를 따를 때 state 및 / 또는 action으로 인한 향후 보상

Given a model of the world

• Markov Processes
• Markov Reward Processes (MRPs)
• Markov Decision Processes (MDPs)
• Evaluation and Control in MDPs

복습 - Markov Property란?

• t: timestamp에 대해 다음이 성립한다.

$\text{State s is markov}\iff p(s_{t+1}|s_t,a_t)=p(s_{t+1}|h_t,a_t)$

• 미래의 state는 과거의 주어진 state에 independent하다

Markov Process or Markov Chain

• Markov process는 random state의 sequence로 볼 수 있다
• 물론 각 state의 전환마다 markov의 속성(State s is markov)을 만족한다
• Markov Chain의 timestamp 개념이 추가된 것이 markov process이다.

Markov process의 정의

• S는 state s의 집합이다 $s \in S$
• P는 dynamic/transition model이고 $p(s_{t+1}=s'|s_t=s)$를 나타낸다.
• Note:아직 여기서 reward, action model는 추가되지 않았다
• S의 크기가 N이면, P는 다음과 같은 matrix로 나타낼 수 있다

$P=\begin{pmatrix}P(s_1|s_1)&P(s_2|s_1)&\dots&P(s_N|s_1)\\P(s_1|s_2)&P(s_2|s_2)&\dots&P(s_N|s_2)\\\vdots&\vdots&\ddots&\vdots\\P(s_1|s_N)&P(s_2|s_)n&\dots&P(s_N|s_N)\\\end{pmatrix}$

• P는 state s에서 state s'으로 전환될 수 있는 확률을 나타낸다.

예시

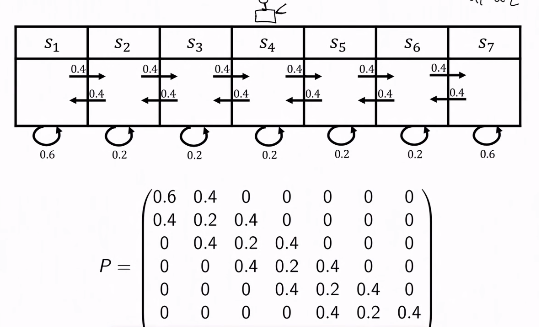
• mars rover는 1번 state부터 7번 state까지 존재하는데, 각 state에서 자기 자신 혹은 인접한 state로만 전환될 수 있다고 가정하면 P는 그림의 것과 같다.
• state의 sequence는 4, 5, 6, 7, 7, 7, ... 과 같이 나타낼 수 있다.
• 만약 mars rover가 첫번째 state일때, 다음 timestamp의 state는 다음과 같이 계산할 수 있다

$\begin{bmatrix}1&0&0&0&0&0&0\end{bmatrix}P=\begin{bmatrix}0.6\\0.4\\0\\0\\0\\0\\0\end{bmatrix}$

Markov Reward Process(MRP)

• Markov Reward Process는 Markov Chain에 reward 개념을 추가한 것이다.

MRP의 정의

• S는 state s의 집합이다 $s \in S$
• P는 dynamic/transition model이고 $p(s_{t+1}=s'|s_t=s)$를 나타낸다.
• R은 reward function이다. $R(s_t=s)=E[r_t|s_t=s]$
  • state s에서 받을 수 있는 reward의 평균값!
• Discount factor $\gamma \in [0,1]$
• 여기서 action은 고려하지 않는다. 아직 action에 의해 reward function이 정의되지 않았다.

예시

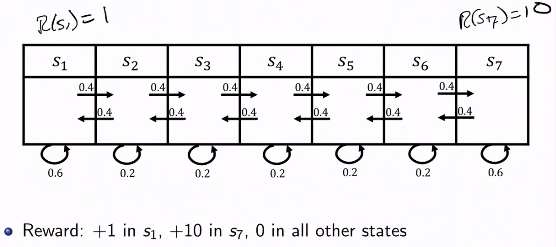
• 1번과 7번 state에 대해서 1과 10의 reward를 정의했다

Return & Value Function

Horizon의 정의

• agent가 얼마나 많은 시간동안 활동할 것인가?를 나타낸다.
• timestamp의 범위는 유한하거나 무한하다.
• timestamp가 유한한경우, finite Markov reward process라 한다.

Return의 정의 (MRP에 한해서)

• discounted sum of rewards from time stemp t to horizon

$G_t=r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\gamma^3 r_{t+3}+\dots$

• return 값은 현재의 timestamp뿐만 아니라, 미래의 timestamp의 return 값도 신경쓴다.

State Value Function의 정의 (MRP에 한해서)

• state s에 대해 받을 수 있는 return 값의 기대값

$V(s)=E[G_t|s_t=s]=E[r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\gamma^3 r_{t+3}+\dots|s_t=s]$

예시 - gamma

• $\gamma=0$: 현재의 reward만 중요성을 지닌다.
• $\gamma=1$: 미래의 reward가 현재의 reward와 동일한 중요성을 지닌다.
  • 만약 episode length가 finite이면 $\gamma=1$을 사용할 수 있다.
  • infinite이면 무한하게 발산하기 때문에 사용 불가능

예시 - mars rover

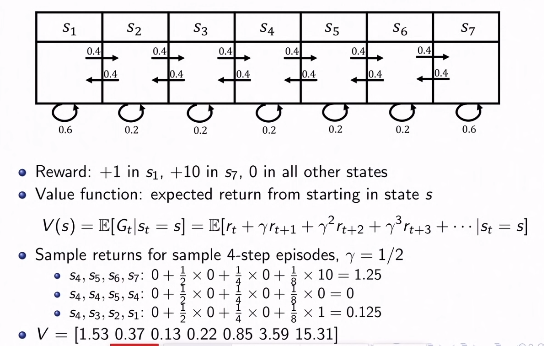
• 주어진 sequence에 대해 return 값을 계산해볼 수 있다.
• 이를 확장해서 각 state에 대한 return 값의 기대값을 나타내는 V를 계산할 수 있을까?

Computing the value of Markov Reward Process

• V가 수렴이 되었다고 가정하면 다음과 같이 유도할 수 있다.

$V(s) = R(s)+\gamma \sum_{s'\in S}P(s'|s)V(s')$

• s에서 오는 즉각적인 보상과 - $R(s)$
• s'에서 오는 미래의 보상으로 구성되어있다 - $\gamma \sum_{s'\in S}P(s'|s)V(s')$
• 위의 식을 모든 s에 대해 계산한 후, matrix notation으로 표기하면 다음과 같다

$V=R+\gamma PV\\(I-\gamma P)V=R\\V=(I-\gamma P)^{-1}R$

• 위 공식에서는 inversion이 가능하다는 보장이 있어야 한다.
• 위 방식처럼 계산시, matrix inversion을 해야하기에 시간복잡도로 N^3이다.

Iterative Algorithm for Computing Value of MRP

• 수렴되기 전 V는 다음의 알고리즘으로 수렴시킬 수 있다.

• Dynamic programming이 이용된다.

• V의 모든 원소를 0으로 initialize로 한다.

• For k = 1 until convergence

  • For all s in S

    $V_k(s)=R(s)+\gamma\sum_{s'\in S}p(s'|s)V_{k-1}(s')$

Markov Decision Process

• 앞의 markov reward process에 action의 개념을 추가한다

MDP의 정의

• S는 state s의 집합이다 $s \in S$
• A는 action a의 집합이다. $a\in A$
• P는 dynamic/transition model이고 $p(s_{t+1}=s'|s_t=s, a_t=a)$를 나타낸다.
• R은 reward function이다. $R(s_t=s, a_t=a)=E[r_t|s_t=s, a_t=a]$
• Discount factor $\gamma \in [0,1]$
• MDP를 tuple로 나타내면 $(S, A, P, R, \gamma)$

예시

state에서 왼쪽으로 가는 행위를 a_1, 오른쪽으로 가는 행위를 a_2라 하면 다음과 같이 나타난다.

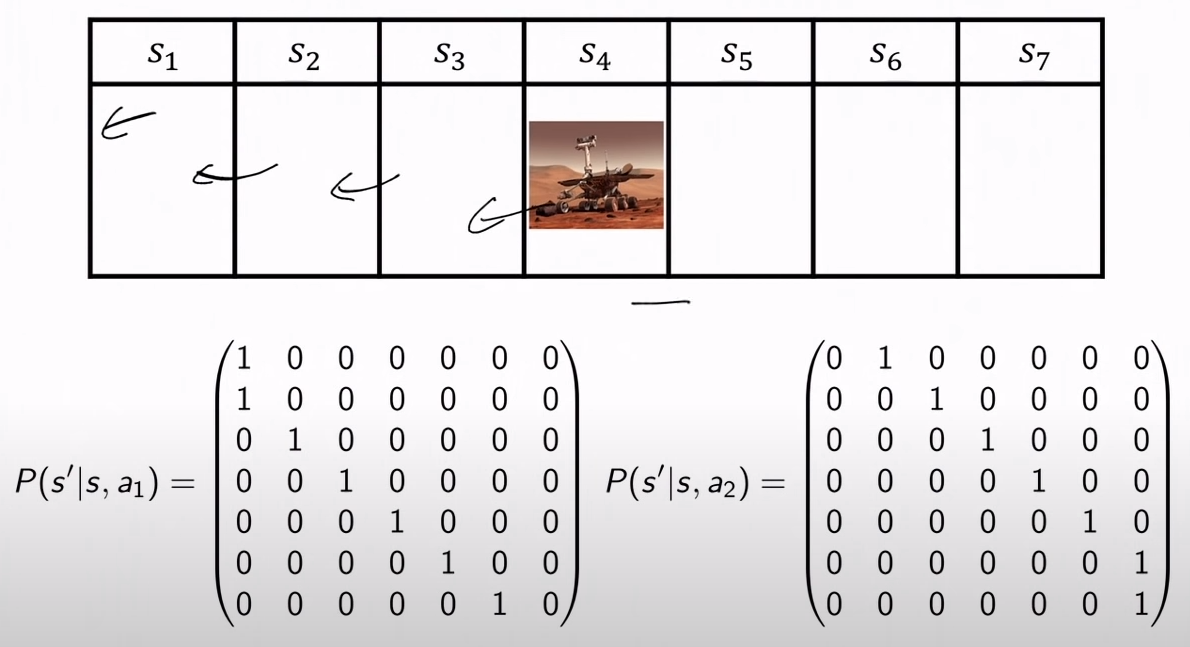
MDP Policies

• policy라는 말 그대로 각 state에서 어떤 action을 취하는지에 대한 것이다.

$\pi(a|s)=P(a_t=a|s_t=s)$

• policy는 determinitstic일수도, stochastic일수도 있다.

MDP + Policy

• MDP + $\pi(a|s)$ = MRP와 같다.
• $MRP(S, R^\pi, P^\pi,\gamma)$로 나타내고, R과 P는 다음과 같다.

$R^\pi(s)=\sum_{a\in A}\pi(a|s)R(s,a)\\P^\pi(s'|s)=\sum_{a\in A}\pi(a|s)P(s'|s,a)$

• Rπ 및 Pπ로 MRP를 정의하면, 앞서 MRP에서 사용되던 동일한 수식을 사용하여 MDP에 대한 정책 값을 평가할 수 있다.

MDP Policy Evaluation, Iterative Algorithm

• value function을 구하는 알고리즘에 policy 개념을 적용하면 다음과 같다.

• V의 모든 요소를 0으로 초기화한다

• For k = 1 until convergence(수렴)

  • For all s in S

    $V_k^\pi(s)=r(s,\pi(s))+\gamma\sum_{s'\in S}p(s'|s,\pi(s))V^\pi_{k-1}(s')$

• Bellman backup이라 불리기도 한다.

MDP Control

• policy를 학습하는 내용은 아직이다
• optimal policy가 무엇인지를 결정해야한다. 이는

$\pi^*(s)=arg\;\underset {\pi}{max}\;V^\pi(s)$

• 만약 optimal value function이 유일하게 존재한다면,
• MDP의 optimal policy와 infinite horizon finite state MDP 문제는 결정적이다.
  • 이들은 결정적이고
  • Stationary하다: 어느 timestamp든 이에 구애받지 않는다
    • (infinite horizon이기 때문!)
  • 그러나, optimal policy는 유일하지 않을 수 있다(같은 policy가 max 값의 value를 지닐 수 있기 때문)
• 그래서 이 optimal policy를 어떻게 찾을것인가?

Policy Search

• 가장 optimal policy를 찾아야 하는데, deterministic policy는 총 $|A|^{|S|}$가지가 가능하다 (각 state마다 action을 정해야 하므로)
• 보통 가능한 모든 policy에 대해 계산 후 결정하는것보다 policy iteration이라는 기법을 사용하면 효율적으로 optimal policy를 찾을 수 있다
• 그래서 policy iteration이 무엇인가?

MDP Policy Iteration

policy iteration은 다음의 알고리즘을 따른다.

• i = 0로 초기화
• 각 state에 대해 $\pi_0(s)$를 무작위로 초기화한다
• while $i == 0\;or\;||\pi_i-\pi_{i+1}||>0$ (policy가 개선됬는지 알아보기 위해 L1-norm을 사용한다)
  • (policy가 개선되지 않을때까지 policy를 개선한다)
  • $V^\pi$←MDP V function policy evaluation of $\pi_i$
  • $\pi_{i+1}$←Policy improvement
  • i = i+1

이 알고리즘에서 두가지 의문이 생긴다.

1. 요약하면 policy가 좋아질때까지 iteration을 돌린다는건데, 과연 이 iteration을 통해 optimal policy에 도달할 수 있을까?
2. iteration을 통해 오히려 안좋아질수도 있는거 아닌가?

State-Action value Q

• policy $\pi$가 좋은지, 안 좋은지를 파악하기 위해 수치화된 값이 필요한데, 이곳에 이용되는 값이 바로 State-Action value (Q로 표기)이다.
• state s에서, action a를 한 다음, policy $\pi$를 따를때 그 value가 얼마나 될 것인가를 나타낸다

$Q^\pi(s,a)=R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V^\pi(s')$

Policy Improvement

각 iteration마다 Q를 이용한 policy improvement는 다음과 같다.

• 모든 S의 원소 s, A의 원소 a에 대해 Q를 계산한다.

  $Q^{\pi_i}(s,a)=R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V^{\pi_i}(s')$

• 새로운 policy에서 state s에 대한 action a는 다음과 같이 결정한다. (가장 큰 Q 값을 가지는 s, a 쌍을 설정)

$\pi_{i+1}(s)=arg\;\underset {a}{max}\;Q^{\pi_i}(s,a)\;\;\forall s\in S$

여기서 우리는 policy가 점차 좋아짐을 알 수 있는데, 그 이유는

새로 행하는 행동 a는 전의 policy인 $\pi_i(s)$와 같거나 다를텐데

• 같은 경우 Q값은 동일할 것이고
• 다른 경우 $\pi_i(s)$보다 좋은 행동으로 $\underset {a}{max}\;Q^{\pi_i}(s,a)$에서 선택된 경우이다.
• 따라서 $Q^{\pi_{i}}(s,a)\geq Q^{\pi_{i}}(s,\pi_i(s))$가 성립한다.

Delving Deeper Into Policy Improvement Step

• 이제 이 Q function에 대해 좀더 알아보자..!

$Q^{\pi_i}(s,a)=R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V^{\pi_i}(s')$

$\underset{a}{max}\;Q^{\pi_{i}}(s,a)\geq Q^{\pi_{i}}(s,\pi_i(s))=R(s,\pi_i(s))+\gamma\sum_{s'\in S}P(s'|s,\pi_i(s))V^{\pi_i}(s')\;\text{(by definition)}$

• 위의 수식에서 policy의 가치는 항상 단조증가함을 보일 ****수 있다. 증명은 다음 단락을 참고하라
• 즉, 새로운 policy는 예전의 policy보다 좋거나 같다

Monotonic Improvement in Policy

• 먼저 policy에 대한 단조증가의 정의는 다음과 같다.

$V^\pi_1\geq V^\pi_2:\;V^\pi_1(s)\geq V^\pi_2(s),\forall s\in S$

• proof(참고)

$V^{\pi_i}(s)\leq \underset{a}{max}Q^{\pi_i}(s,a)\\= \underset{a}{max}\;(R(s,a)+\gamma \sum_{s' \in S}P(s'|s,a)V^{\pi_i}(s'))\\=R(s,\pi_{i+1}(s))+\gamma \sum_{s'}P(s'|s,\pi_{i+1}(s))V^{\pi_i}(s')\;\text{(by def of new policy)}\\\leq R(s,\pi_{i+1}(s))+\gamma \sum_{s'}P(s'|s,\pi_{i+1}(s))\underset{a}{max}(s', a')\;\text{(by def)}\\=V^{\pi_{i+1}}(s)$

Policy Iteration: check!

• 만약 policy가 바뀌지 않는다면, 여기서 바뀔 수 있는가?
  • 아니다! policy가 바뀌지 않는 경우 $\pi_i-\pi_{i+1}=0$이 되므로, iteration이 진행되지 않는다.
• policy iteration의 maximum number는?
  • policy는 $|A|^{|S|}$개 존재하는데, policy는 단조증가하고 동일한 policy는 두번 올 수 없으므로, policy의 개수만큼 iteration이 가능하다.

MDP: Computing Optimal Policy and Optimal Value

• policy iteration은 horizon이 infinite할때 (남은 timestamp가 무한대)일때 policy를 성능을 측정해가며 점차 개선해나가는 방식이고
  • optimal policy를 알게 되므로 optimal value도 알게 된다.
• Value iteration은 horizon이 k일때 optimal value를 찾아가며 k를 증가시키는 형식이다.
  • optimal value function을 먼저 찾고 그에 따른 optimal policy를 결정짓는다.
  • 주로 state x에서 action a를 하면 state x'으로 가는 확률을 알때 사용하는데... 음.... 모르겠다..
  • 이부분에 대해서는 추후 강의를 들은 후 쓸모가 있으면 수정하도록 하겠다 :(