[Baekjoon] 1654. 랜선 자르기 (이진탐색)

문제 바로가기

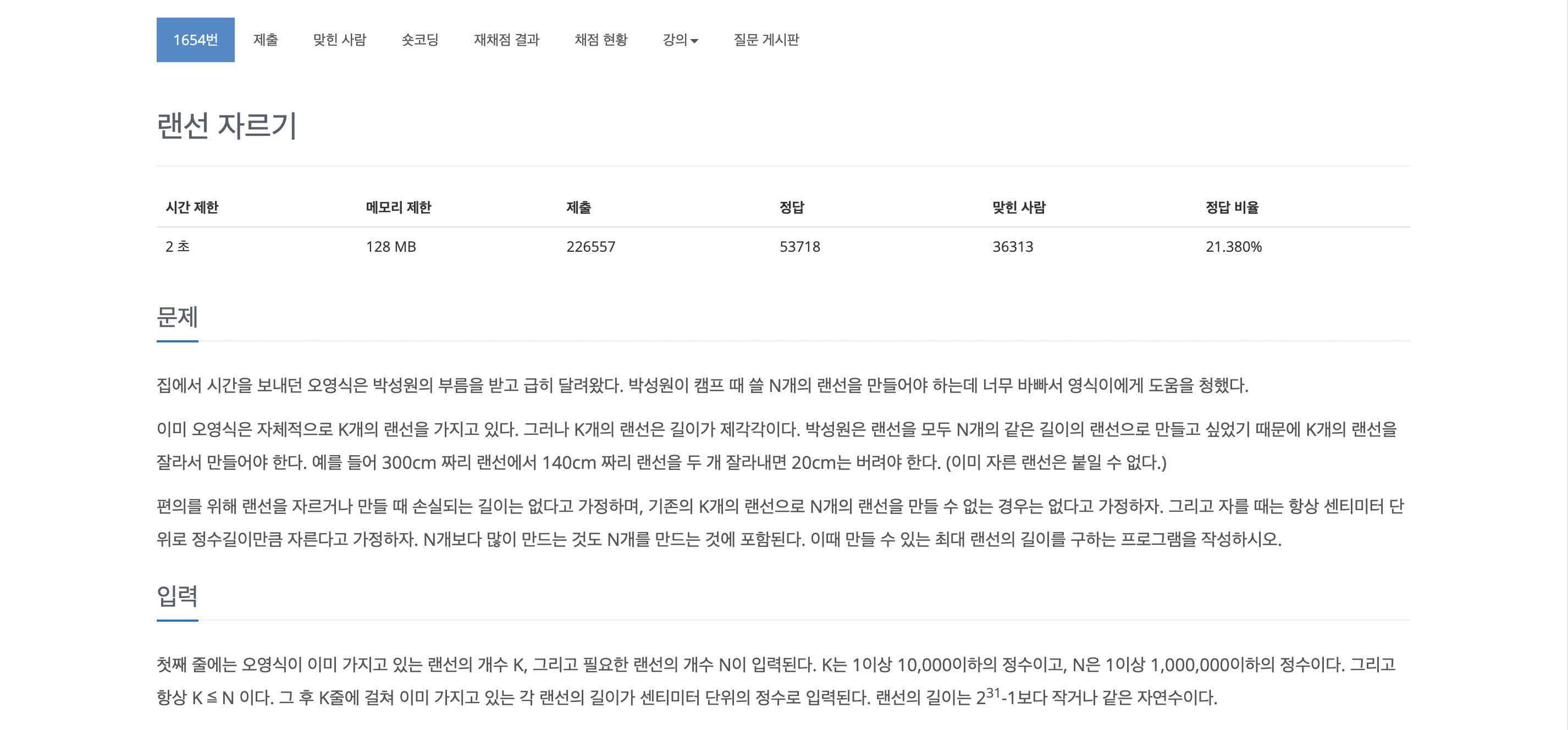
• 길이가 제각각인 K개의 랜선을 가지고 있다.
  $1 \leq K \leq10,000$

• N개의 같은 길이의 랜선을 만들고자 한다.
  $1 \leq N \leq1,000,000$

• 랜선의 길이 $a$라 했을때, $a$는 자연수이며 $a \leq 2^{31} -1$

🔍 풀이

---

풀이 아이디어

• 적절한 길이를 찾을 때까지 랜선의 길이를 반복해서 조정하면 된다.
• 범위가 매우 크므로 효율적인 이진탐색을 이용하여 범위를 좁혀가며 탐색한다.

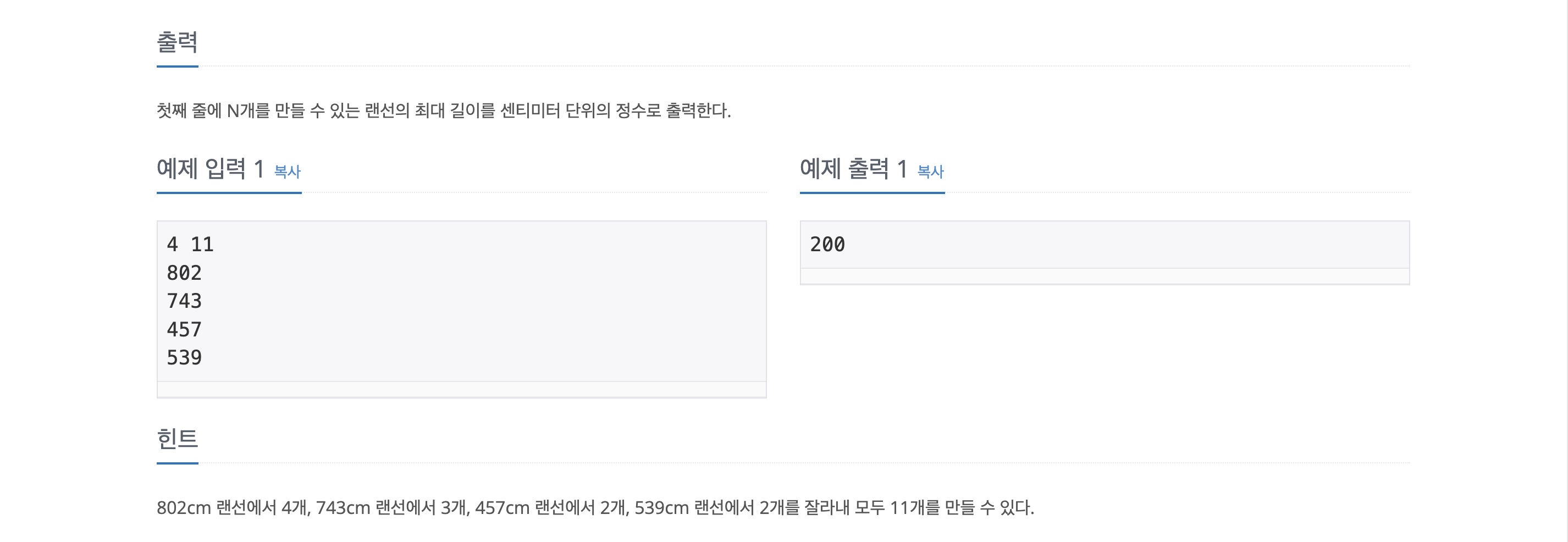
만들 수 있는 랜선의 최대 길이를 $x$ 라 했을 때,
$x$는 가장 긴 랜선의 길이 안에 있어야만 한다.
따라서 1 ~ (가장 긴 랜선의 길이) 만큼 탐색하여 최적의 답을 찾아낸다.

랜선의 길이(탐색 범위)는 1이상 $2^{31} -1$이하의 정수 중 하나이다. 수가 매우크므로 이진탐색을 이용한다. (순차탐색의 경우 시간초과)
큰 수를 보면 가장 먼저 이진 탐색을 떠올리자!

중간점(mid)의 값은 시간이 지날수록 '최적화된 값'을 찾기 때문에 과정을 반복하면서 얻을 수 있는 랜선의 개수가 필요한 랜선의 개수보다 크거나 같을 때마다 결괏값을 중간점(mid)으로 갱신해주면 된다.

💫 Comment

---

'떡볶이 떡 만들기' 와 동일한 유형의 문제
탐색범위가 매우 크므로 이진탐색을 사용해야 함을 알수 있었다.

시행착오
처음엔 이진탐색의 끝end을 '가지고 있는 랜선 중 가장 짧은 랜선의 길이'(min(data)로 두었다.
하지만 필요한 랜선 수 N의 범위는 $1 \leq N \leq1,000,000$ 임을 생각하지 못했다.
만약 필요한 랜선의 수가 1이라면 랜선을 자를 필요없이 '가지고 있는 랜선 중 가장 긴 것'(max(data))을 사용하면 된다.
따라서 최대값 랜선을 end로 두어야 한다.

🔍 코드

---

# 랜선 자르기
import sys

# 입력받기
k, n = map(int, input().split())
data = [int(sys.stdin.readline()) for _ in range(k)]

# 이분 탐색의 처음과 끝
start = 1
end = max(data)

# 만들 수 있는 랜선의 최대 길이를 찾는다.
while start <= end: # start > end가 될때까지 반복

    lan = 0 # 만들 수 있는 랜선의 개수 초기화
    mid = (start + end) // 2 # 이분탐색의 중간

    # mid길이로 랜선을 잘랐을 때 만들어지는 랜선의 개수 구하기
    for i in data:
        lan += i // mid
    
    if lan < n: # 잘린랜선의 개수가 부족한 경우 길이를 줄여본다.
        end = mid - 1
    else: # 만들어진 개수가 필요개수보다 더 크거나 같을때 랜선의 길이를 늘린다.
        result = mid
        start = mid + 1
        
print(result)

🔍 다른 코드

---

# 위의 코드와 동일

	if lan < n:
        end = mid - 1
    # 바뀐 코드
    else: 
        start = mid + 1
        
# 바뀐 코드
print(end)

Reference
이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저, 한빛미디어)