인접행렬 인접리스트

프로그래밍에서 그래프는 크게 2가지 방법으로 표현할 수 있다.

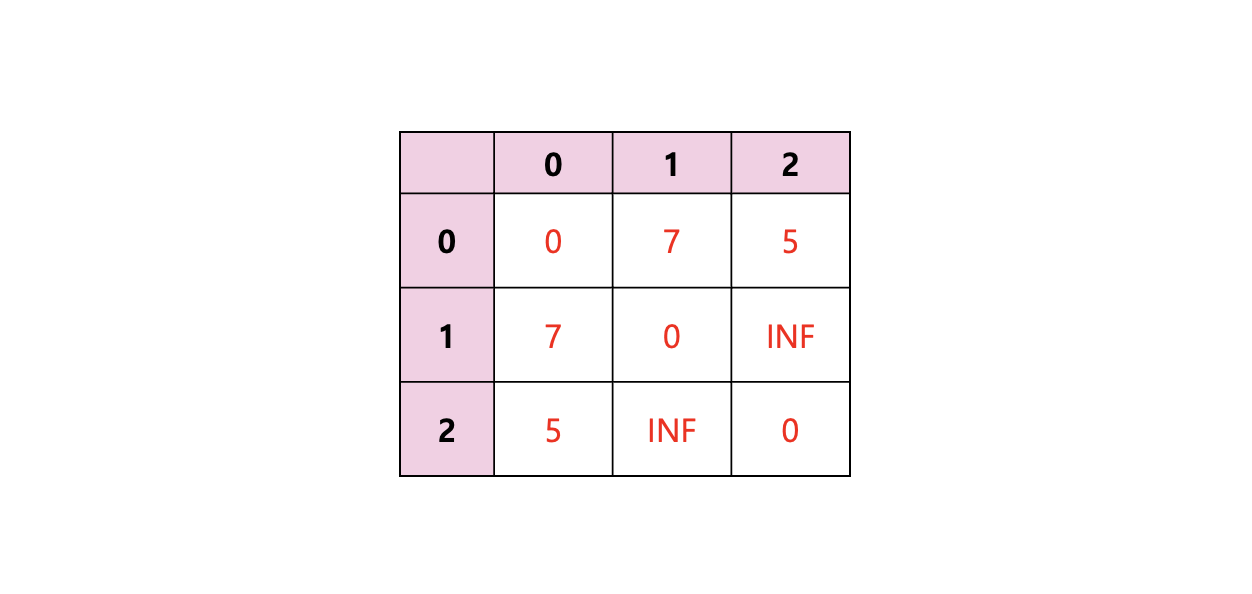
• 인접 행렬 (Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현

#인접 행렬
[[0,7,5], [7,0,999999999], [5,999999999,0]]

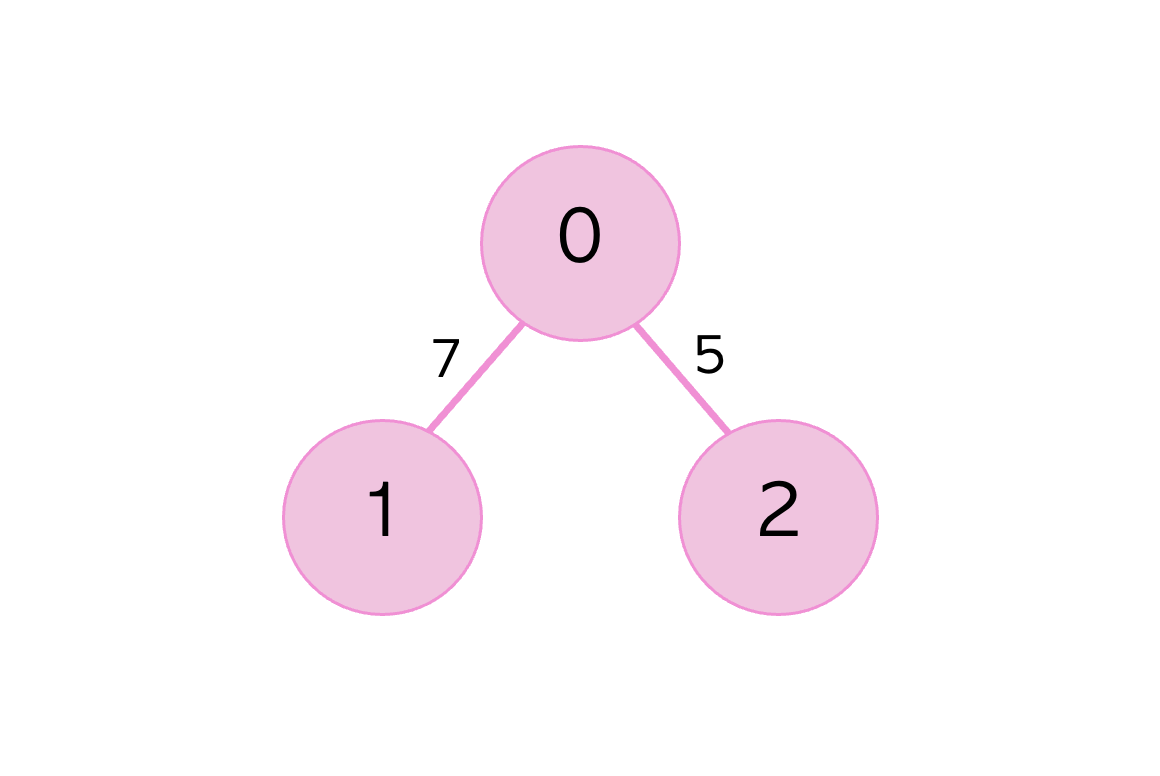
• 인접 리스트 (Adjacency List) : 리스트로 그래프의 연결 관계를 표현

#인접 리스트 
[[(1,7),(2,5)], [(0,7)], [(0,5)]]

#인접 행렬 방식 예제

INF = 999999999 #무한의 비용 선언

#2차원 리스트를 이용해 인접 행렬 표현
graph = [
    [0,7,5],
    [7,0,INF],
    [5,INF,0]
]

print(graph)
#[[0,7,5], [7,0,999999999], [5,999999999,0]]

#인접 리스트 방식 예제

#행이 3개인 2차원 리스트로 인접리스트 표현
graph = [[] for _ in range(3)]

#노드0에 연결된 노드 정보 저장 (노드, 거리)
graph[0].append((1,7))
graph[0].append((2,5))

#노드1에 연결된 노드 정보 저장 (노드, 거리)
graph[1].append((0,7))

#노드2에 연결된 노드 정보 저장 (노드, 거리)
graph[2].append((0,5))

print(graph)
#[[(1,7),(2,5)], [(0,7)], [(0,5)]]

<두 방식의 차이점>

메모리 측면 : 인접 리스트 방식이 더 효율적.

• 인접행렬방식은 모든 관계를 저장하므로 노드 개수가 많을수록 메모리가 불필요하게 낭비된다.
  (ex. 1과 2는 연결되어있지 않아도 '무한'이라는 값으로 저장함.)
• 인접리스트방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용
  (ex. 연결되어있지 않은 1과 2 사이의 정보는 저장하지 않음.)

-> 인접 리스트 방식은 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다. 인접 리스트 방식에서는 연결된 데이터를 하나씩 확인해야 하기 때문.
ex.노드 0과 2가 연결되어있는지 확인할 때 인접리스트방식은 graph[0][2]만 확인하면 되지만 연결리스트방식은 graph[0]에서 연결된 데이터를 앞에서부터 차례대로 확인해야 함.
-> -> 특정한 노드와 연결된 모든 인접 노드를 순회해야 하는 경우, 인접 리스트 방식이 인접행렬 방식에 비해 메모리 공간의 낭비가 적다.